液压电机泵转子支撑方式对转动特性的影响
2013-03-09冀宏孙天健王金林武俊合
冀宏,孙天健,王金林,武俊合
(兰州理工大学能源与动力工程学院,甘肃兰州 730050)
液压电机泵转子支撑方式对转动特性的影响
冀宏,孙天健,王金林,武俊合
(兰州理工大学能源与动力工程学院,甘肃兰州 730050)
液压电机泵主轴比较细,其支撑方式将会直接影响转子的动特性。针对液压电机叶片泵转子系统进行分析,利用Pro/E质量属性分析功能建立电机泵转子系统模型,用ANSYS建立4种不同支撑方式的一维有限元模型,通过转子动力学分析计算,获得临界转速、频率、挠度变化及对应振型。结果表明:不同的支撑方式对电机泵转子的临界转速、固有频率、挠度和刚度具有明显的影响,支撑点接近质心或多点支撑均能显著提高电机泵转子系统刚度。计算结果为电机泵转子系统的设计提供理论依据。
液压电机泵;电机泵转子;支撑方式;挠度;有限元法
液压电机泵是将电机与液压泵融合一体的新型液压动力单元,具有体积小、结构紧凑﹑无外泄漏、噪声小﹑效率高等优点。液压电机泵转子是电动机转子与泵转子的一体复合,电动机功率密度远小于同功率液压泵,因此,前者转子尺寸远大于后者转子,两者的复合转子质量分布、长径比均发生很大变化。为保证电机泵的机械效率和平稳运行,其轴承合理布置成为电机泵结构设计中一个关键共性问题。兰州理工大学课题组设计出液压电机泵——内嵌式液压电机叶片泵动力单元,如图1所示[1-3],其转子系统由电机转子1、主轴2、叶片泵转子3、转子套离心泵4和轴承组成,如图2所示。转子套离心泵嵌入到电机转子内部,通过主轴与叶片泵转子集成为一体,组成电机泵转子。

图1 液压电机叶片泵
由于电机泵转子系统材质的不均匀,以及制造、加工及装配存在的误差等,电机泵转子系统不可避免地存在着质量偏心,再加上工作中产生的热变形以及磨损等现象,使得转子系统质量分布不均匀,可导致转子系统高速旋转时产生不平衡振动。而由回转体的不平衡引起的振动使机械效率降低、载荷增加,导致零部件磨损、疲劳,降低使用寿命,增大噪声。针对液压电机泵自身结构特点,对于液压电机泵的回转体——转子系统来说,在设计、制造、加工及安装等方面就要充分考虑电机泵转子的结构和支撑方式。
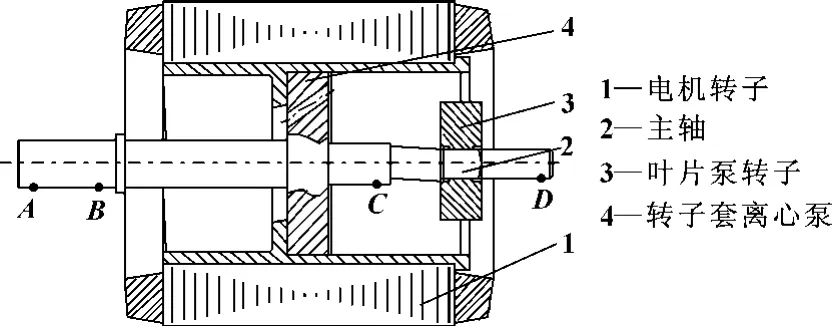
图2 电机泵转子
作者以图1所示的液压电机叶片泵为研究对象,引入转子动力学理论和有限元方法对其支撑方式进行了分析与计算。
1 液压电机叶片泵转子系统的分析
1.1 电机泵转子系统模型的简化与建立
由图1知,由于受到电机叶片泵自身结构空间的限制,主轴相对转子系统来说比较细,显得比较单薄,在设计时必须考虑轴承对主轴支撑点的合理布置。于是,作者对电机泵转子采用了4种支撑方式进行分析,其支撑点分布如图2中A、B、C、D所示,其中点A、B处为滚动轴承,点C、D处为滑动轴承。4种支撑方式名称如表1所示。
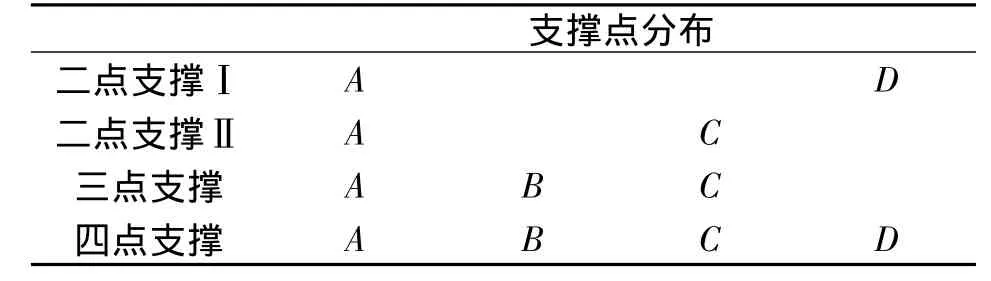
表1 转子系统不同支撑方式
为了便于分析和计算,把电机叶片泵转子系统的转子套离心泵与电机转子 (下文称为电机转子)、叶片泵转子 (下文称为泵转子)看作两个圆盘进行简化。其简化支撑结构如图3(a)、(b)、(c)、(d)所示,电机转子通过主轴与泵转子结合为一体,然后与轴承支撑形成电机泵转子系统。
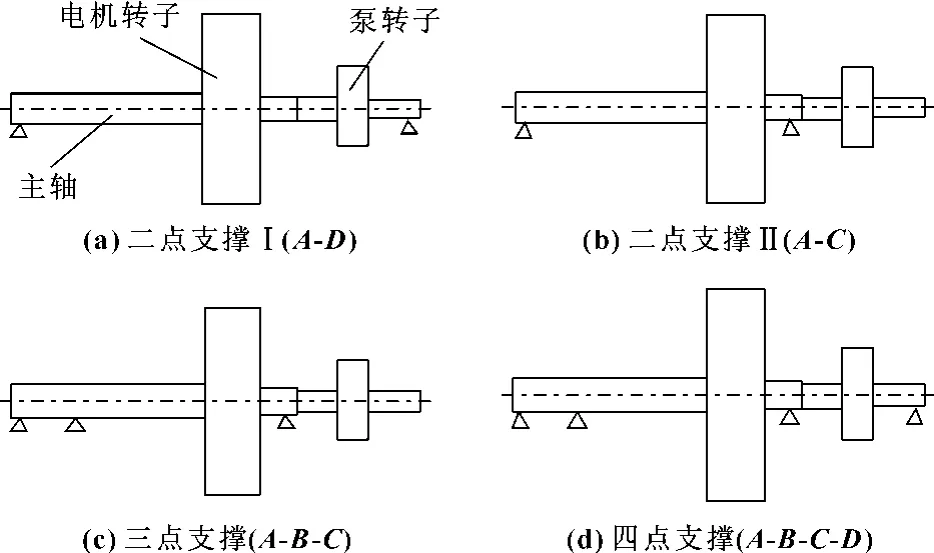
图3 电机泵转子系统简化模型
通过Pro/E中的“分析-模型-质量属性”分别确定出电机转子和泵转子的质心、极转动惯量Jp1和Jp2、直径转动惯量Jd1和Jd2。然后对转子经过质量集总处理,支撑位置在轴承径向中心面与轴承——主轴接触面的交线处。
1.2 电机泵转子系统动力学的分析
在工程实际中,一般的旋转机械如电动机主轴等因抗弯刚度很大都可视为刚性转子[4]。刚性转子和挠性转子的划分没有绝对依据,工程上通常以最低临界转速[5]为分界线。工作转速低于最低临界转速的转子通常称为刚性转子,工作转速高于最低临界转速的转子称为挠性转子。转子系统不平衡质量引起的振动属于强迫振动。
转子系统质量的不平衡,导致质心与主轴轴心的偏离,导致质心与轴心之间产生偏心距e。根据刚性转子平衡品质许用不平衡 (GB9239-88)的规定,由式(1)计算出偏心距e:

式中:G为平衡品质等级(mm/s)。
转子系统转速ω根据公式(2)计算出:

式中:n为转子系统转速(r/min)。
高速旋转的转子零件,由于相对于轴线的质量分布不均匀而产生离心力[6],即惯性力,引起整机的振动。根据动力学定律计算出离心力,其公式表达式为:

式中:e为偏心距(mm);m为总质量(g);ω为等角速度(rad/s);F为离心力(N)
一般来说,一个旋转机械系统的运动微分方程式可以写为[7]:

式中:m为总质量(g);z为z轴方向变量(mm);C为阻尼阵;G为陀螺阵;K为刚度矩阵的对称部分;S为刚度矩阵的不对称部分;F为合力(N)。
在刚性支撑条件下,由于旋转轴在空间中改变方位时,绕主轴高速旋转的转子要表现出抗阻力矩,产生陀螺效应。因此,在考虑陀螺效应时,具有N个圆盘的转子系统有4N个自由度。液压电机叶片泵转子系统具有两个圆盘——电机转子和泵转子。该系统具有8个自由度。设圆盘质量为mi、直径转动惯量Jdi、极转动惯量Jpi(i=1,2),抗弯刚度EI,针对4种支撑方式分别建立坐标系,其中,二点支撑Ⅱ的模型坐标系如图4所示。
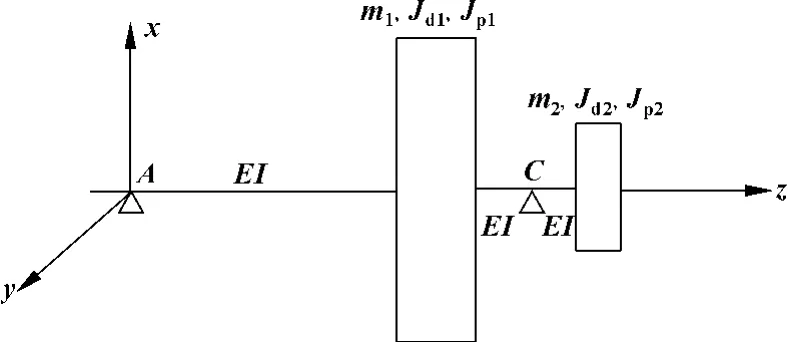
图4 二点支撑Ⅱ模型坐标系
2 液压电机叶片泵转子系统的计算
在ANSYS软件中采用一维模型计算分析电机叶片泵转子系统,假设与简化如下:
(1)使用结构质点 (MASS21)分别模拟电机转子、泵转子的点单元。MASS21单元具有分别沿x、y、z轴位移及绕其转动的6个自由度。点单元的质量和转动惯量以实常数定义。
(2)使用3-D线性有限应变梁 (BEAM188)模拟主轴。BEAM188是一个二节点的三维线性梁,每个节点上有6个或7个自由度,自由度数目由KEYOPT(1)来控制。当KEYOPT(1)=0(默认)时,每节点有6个自由度,分别沿x、y、z轴位移及绕其转动。KEYOPT(1)=0时,会添加第7个自由度 (横截面的翘曲),是铁摩辛柯 (Stephen P Timoshenko)梁,考虑剪切变形。
(3)使用弹簧阻尼组合单元 (COMBIN214)模拟主轴上的轴承,轴承模型如图5所示,虚线圆代表轴承的外圈,弹簧与阻尼器的组合体代表钢球,实线小圆代表主轴。COMBIN214由两个节点I、J组成,每个节点有2个自由度,不考虑弯曲和扭转。单元有4个刚度系数K11、K12、K21、K22和4个阻尼系数C11、C12、C21、C22。作者在模拟轴承单元时,忽略阻尼,并假设轴向刚度对称,其中,两个滑动轴承以滚动轴承代替。轴承刚度由标准轴承在线弹性范围内的赫兹(Hertz)接触理论径向变形公式 (5)导出:
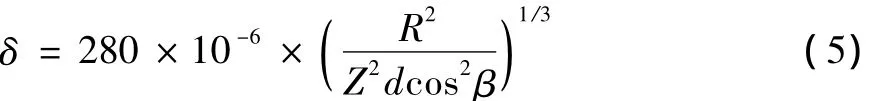
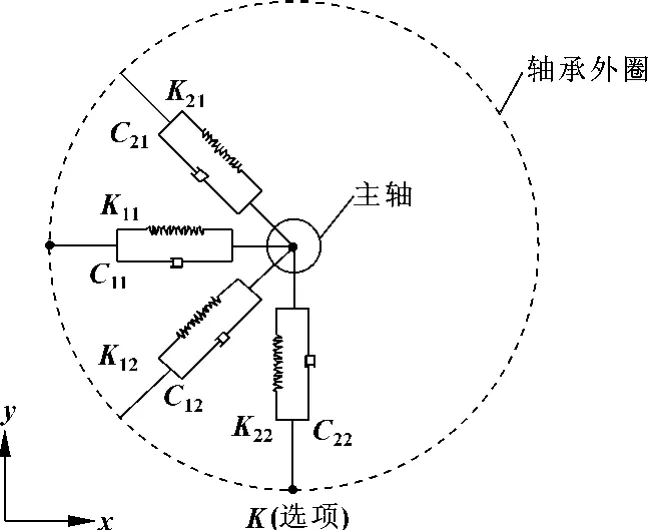
图5 轴承模型
两边求微分得出刚度公式 (6):
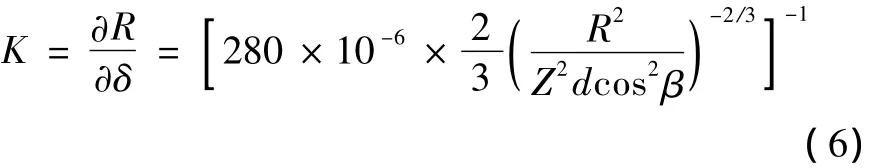
式中:δ为轴承径向变形 (mm);R为径向载荷 (10 N);Z为为钢球数目;d为钢球直径 (mm);β为滚动体接触角。这里根据轴承所在主轴处的直径查轴承标准选取轴承型号,并由式 (6)计算得出A、B点轴承刚度为9.17×107N/m,点C为5.95×107N/m,点D为5.20×107N/m。
转子系统的材料属性分别为:杨氏模量E=2.06×1011Pa,密度ρ=7 800 kg/m3,泊松比ν=0.3。主轴为实心轴。计算中考虑转子材料的阻尼,阻尼取为4×10-5,考虑陀螺力矩的影响。
建立该转子系统4种一维模型分别如图6中的(a)、(b)、(c)、(d)所示,水平实线代表主轴,竖短实线代表选取的相应轴承,实线上的星号分别代表电机转子和泵转子,线上的数字为节点号。进行网格划分,选择网格划分工具面板Size中Controls,在Size选项中把网格单元尺寸设置为0.02。

图6 一维模型
定义电机泵转子系统边界条件:对转子系统沿主轴轴线的平动位移和绕主轴轴线的转动位移进行约束;对模拟轴承外圈进行全约束;考虑陀螺效应的作用,转子系统会出现正进动和反进动,在这里只对正进动进行分析。
图7—12为约束状态下各种支撑方式的第一阶、第二阶、第三阶模态振型和转子系统对应频率轨迹图。虚线代表主轴初始位置,弯曲实线代表主轴振动实际位置,曲线上星号表示电机转子和泵转子。
由图7与图8知:一阶振型中,二点支撑Ⅰ节点表现为同向偏移,最大偏移位置在电机转子部位;四点支撑节点表现为异向偏移,最大偏移位置在电机转子部位;二点支撑Ⅱ、三点支撑节点位置偏移形状基本相似,电机转子、泵转子分别在主轴轴线初始位置两侧,表现为异向偏移,其中,二点支撑Ⅱ、三点支撑最大偏移位置在主轴轴线的左端部位。
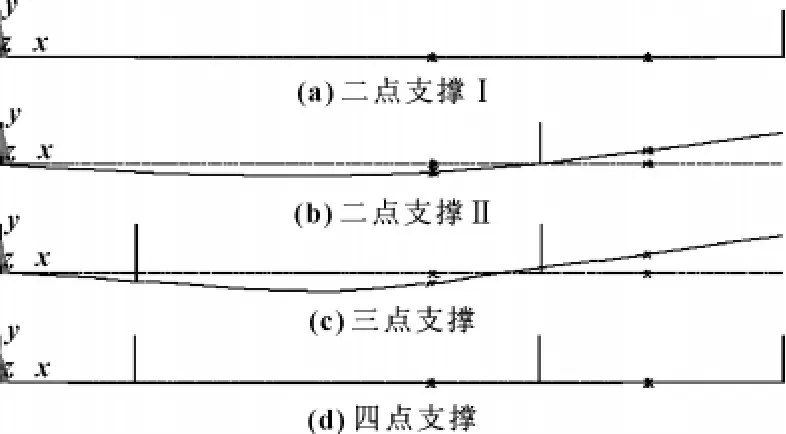
图7 一阶振型对比
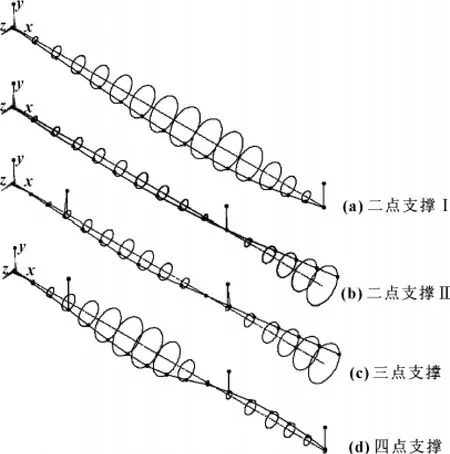
图8 转子系统一阶频率轨迹图
由图9与图10知:二阶振型中,二点支撑Ⅰ、二点支撑Ⅱ、三点支撑与一阶振型基本相似;四点支撑节点表现为同向偏移,最大偏移位置在电机转子部位。
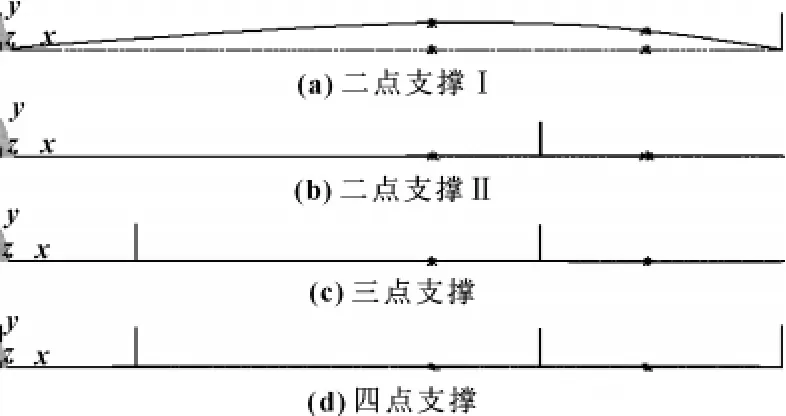
图9 二阶振型对比
由图11与图12知:三阶振型中,二点支撑Ⅰ的电机转子与泵转子分布在主轴轴线初始位置两侧,表现为异向偏移,最大偏移位置在靠近主轴左端位置;二点支撑Ⅱ的节点同向偏移,最大偏移位置在主轴右端位置;三点支撑的节点表现为异向偏移,最大偏移位置在电机转子部位;四点支撑节点为同向偏移,最大偏移位置在中间部位。
对比图7—12可知:从一阶振型到三阶振型以及相应轨迹图,四点支撑方式的节点最大偏移位置变化比较稳定,其他3种变化明显。
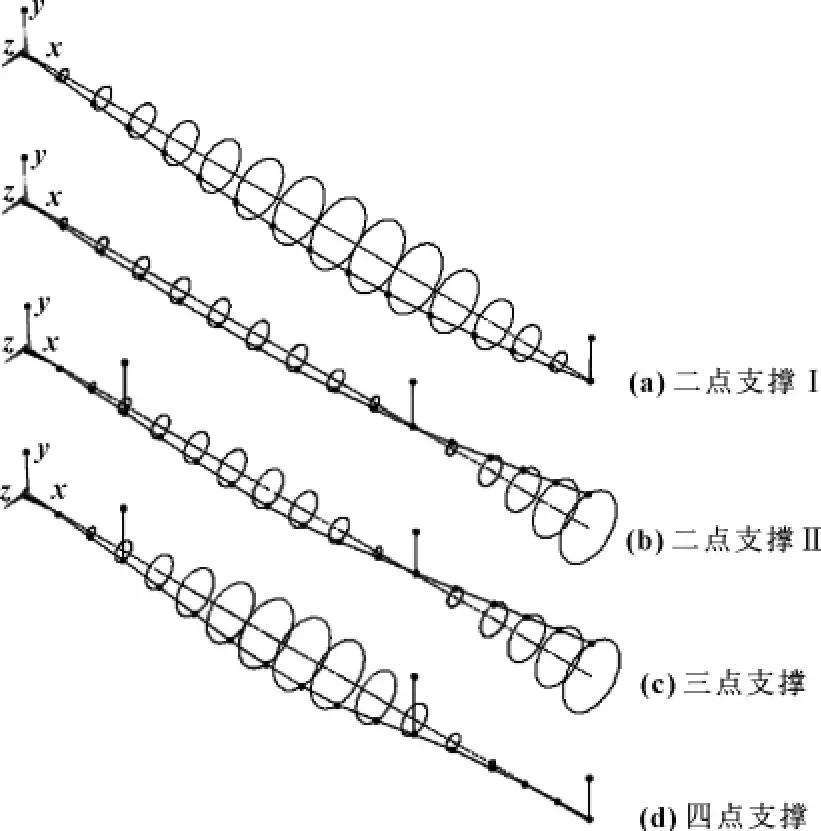
图10 转子系统二阶频率轨迹图

图11 三阶振型对比
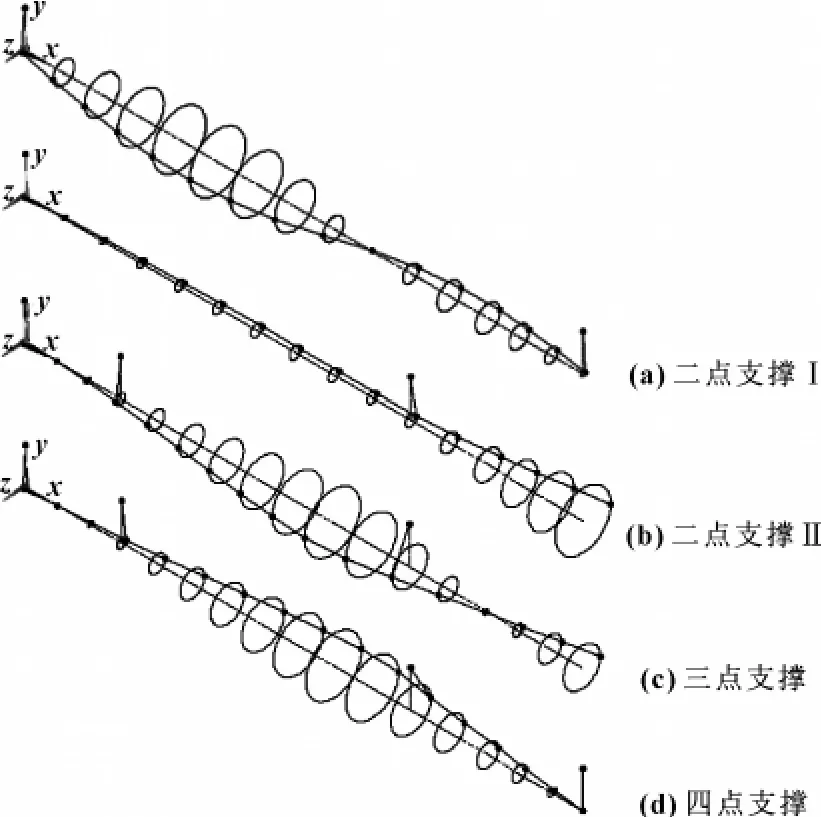
图12 转子系统三阶频率轨迹图
4种支撑方式下转子系统的前3阶临界转速如表2所示;前3阶固有频率如表3所示;对电机泵转子系统输入1 460 r/min的转速,获得前3阶最大挠度值,如表4所示。
由表2知:在这4种支撑方式中,前3阶临界转速呈递增趋势,二点支撑Ⅰ的临界转速最低,四点支撑的临界转速最高。
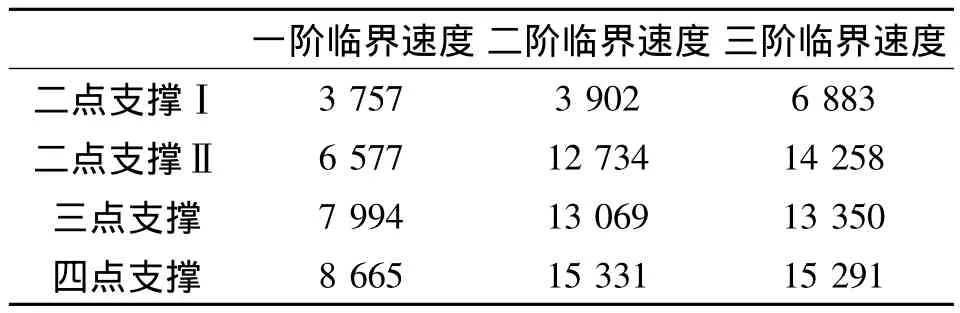
表2 转子系统不同支撑方式下的临界转速计算结果r/min
由表3知:在这4种支撑方式中,固有频率呈递增趋势,二点支撑Ⅰ的固有频率最低,四点支撑的固有频率最高。
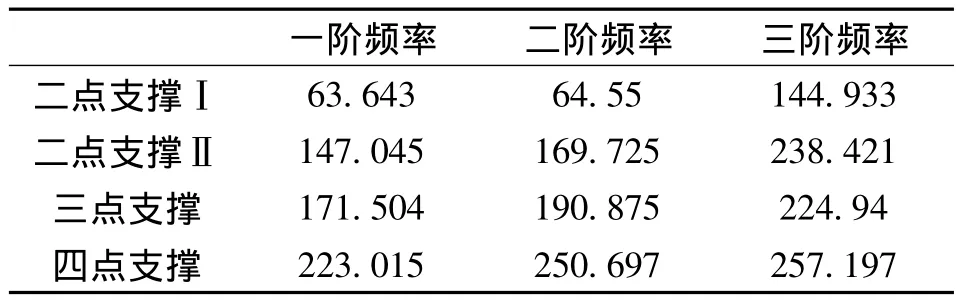
表3 转子系统不同支撑方式下的固有频率计算结果 Hz
由表4知:从一阶、二阶到三阶中,四点支撑挠度值变化比较平缓,三点支撑次之,二点支撑Ⅰ挠度值变化最大,二点支撑Ⅱ挠度值较大,变化小。
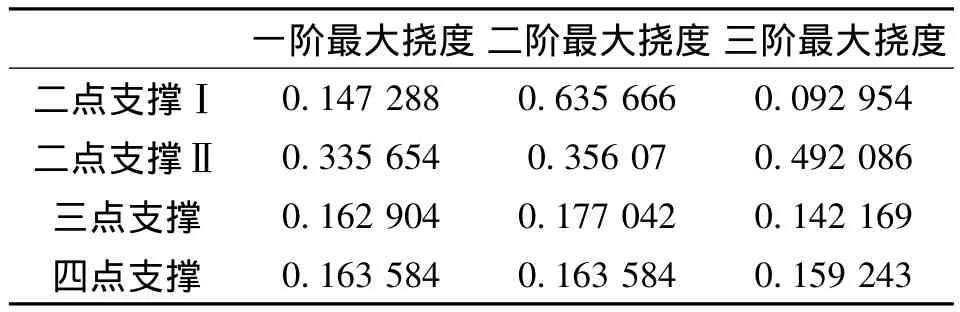
表4 转子系统不同支撑方式下的挠度计算结果
3 结论
采用有限元法分别计算出液压电机叶片泵转子4种支撑方式下的转子临界转速、频率、挠度,为电机泵转子的设计提供理论参考。
(1)支撑方式不同,电机泵转子系统的刚度不同。支撑点接近质心或多点支撑均能显著提高电机泵转子系统刚度。相同阶数下,临界转速和固有频率越低,则刚度越小,反之,则刚度越大。电机泵转子系统的刚度从二点支撑Ⅰ、二点支撑Ⅱ、三点支撑、四点支撑依次增大。刚度大的转子系统,在工作时,挠度小,转动平稳性好。
(2)针对文中研究的电机叶片泵,转子系统实际工作转速为1 460 r/min左右,对比4种支撑方式下的一阶临界转速,电机泵转子的转速均低于一阶临界转速,4种支撑方式下,电机泵转子均符合刚性转子要求。
(3)从挠度值在一阶、二阶、三阶中的变化中知,支撑点布置的方法不同,其最大挠度与变化不同,支撑点接近质心或多点支撑时,挠度变化比较平稳。支撑点越多,对加工、装配的精度要求也相应提高。
【1】冀宏,孙磊,王峥嵘,等.一种电机内嵌叶片泵:中国,200720186800.2[P].2008 -11 -05.
【2】冀宏,丁大力,王峥嵘,等.液压电机泵内置孔板离心泵的流场解析与优化[J].机械工程学报,2009,46(6):199-205.
【3】冀宏,李志峰,王峥嵘,等.液压电机叶片泵样机的性能试验[J].农业机械学报,2009,41(11):48 -51,56.
【4】唐善华.刚性转子动平衡测试原理与实现[J].武汉工业学院学报,2007,26(2):36 -39.
【5】曹景芳,李生伟.火力发电厂刚性转子的现场动平衡技术[J].华电技术,2010,32(12):34 -36,39.
【6】周文君,张广阔,宋丽华.刚性转子平衡技术初探[J].煤矿机械,2010,31(12):94 -96.
【7】王海朋,黛永,张志清,等.基于ANSYS的发动机转子临界转速计算[J].航空发动机,2009,35(5):30 -31,51.
Influence of Rotor SupportWay on Dynam ic Characteristic in the Hydraulic Motor Pump
JIHong,SUN Tianjian,WANG Jinlin,WU Junhe
(College of Energy and Power Engineering,Lanzhou University of Technology,Lanzhou Gansu 730050,China)
The supportway of the integrated rotor in hydraulicmotor pump has a direct influence on dynamic characteristics of rotor due to its slender shaft.The rotor system of hydraulic motor pump was analyzed.A rotor system model of hydraulic motor pump was built by the function ofmass property analysis in Pro/E and one-dimensional finite elementmodels of four different supportways were set up by ANSYS.The rotor critical speed,frequencies,deflection change and correspondingmodes were obtained by analysis and calculation of rotor dynamics.The results show that differentsupportways have an obvious influence on critical speed,natural frequencies,deflection and stiffness of the rotor.The stiffness of the rotor is increased markedly when the support point is closed to the rotor centroid orwith several supportpoints.The computational results provide theoreticalguidance for the design of the rotor system of hydraulic motor pump.
Hydraulicmotor pump;Motor pump rotor;Supportway;Deflection;Finite elementmethod
TH137
A
1001-3881(2013)9-001-5
10.3969/j.issn.1001 -3881.2013.09.001
2012-04-02
国家自然科学基金项目 (51075194);甘肃省科技支撑计划 (1011GKCA041)
冀宏 (1972—),男,教授,博士研究生导师,研究方向为现代液压元件与工程机械液压技术。E-mail:jihong@lut.cn
