方腔内冷热微管自然对流换热的多格子LBM研究

焦文静，戴传山，王秋香

（天津大学机械学院，中低温热能高效利用教育部重点实验室，天津300072）

换热器是将热流体的部分热量传递给冷流体的设备，广泛地应用于石油、化工、冶金、动力、核能等工业部门及国防工程中。换热器作为化工过程中必不可少的单元设备，其材料及动力消耗占整个工艺设备消耗的30%左右［1］。换热器的设计水平往往直接影响着工业的投资效益和能效［2］，使得换热器的强化传热技术越来越受到重视。如何提高换热器的性能，一直是换热器研究和开发的目标［3－4］。换热器微型化，不仅仅意味着节约材料和空间，更重要的是与常规尺度的换热器相比，实现相同目标的同时，通常情况下可以大幅度的缩减所消耗的能量，具有高传热系数、高表面积体积比、低传热温差、低流动阻力等优点，与普通换热器相比，其单位体积传热系数高达几十到几百MW／（m3·K），比普通换热器要高12个数量级。器件装置微型化的强大发展趋势推动了微型换热器技术的迅猛发展，使其成为热能传递与动力转换领域的一个重要研究方向［5］。微尺度换热器的特征尺度在微米到亚毫米尺度范围内，微尺度传热与流动问题机理非常复杂，需要对其进行大量的理论模拟与实验研究。格子波尔兹曼方法（LBM）是20世纪80年代新兴发展起来的一种数值计算方法，具有粒子特性的先天优势，相比其它常规的数值方法更容易处理复杂的理论模拟问题［6－7］。在LBM数值模拟中，大多采用均匀网格［8－10］对模型进行剖分，这虽然有利于LBM的实现，但在计算精度和计算代价的问题上限制了其应用范围。均匀网格模拟的收敛速度受网格步长的制约：网格越密，精度相对较高但收敛速度越慢。为了解决这个问题，多格子波尔兹曼方法被学者提了出来［11］。对复杂流动问题，在靠近流场边界的区域其物理量一般变化复杂、剧烈，对这些区域应该采用较细的网格来保证计算精度；而在远离边界的区域，物理量变化相对平缓，采用较粗的网格可以在不影响精度的前提下大大提高收敛速度。所以，探讨根据物理量变化的剧烈程度划分成粗细不同的网格，对实现高效的LBM数值模拟计算有着重要的现实意义。

1 多格子LBM

这种方法最先由Yu［11］提出。多格子LBM对处理复杂边界非常有效，能够较好的满足精度和高效的双重要求。这种方法是将计算区域分为不同的块，各个块之间通过边界相互交换信息，交换的信息必须满足一定的关系，从而使质量、动量守恒，使作用力能连续的通过边界。

通过两块系统来说明多格子LBM方法［12］。两种格子的空间步长比率m定义如式 （1）。

Δxc、Δxf分别是粗网格和细网格的空间步长。流体的黏度由式 （2）求出。

为了满足黏度为常数，粗网格的松弛时间τc和细网格的松弛时间τf必须满足式 （3）。

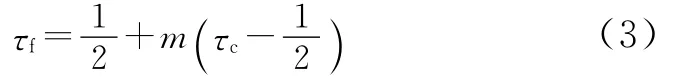
同时为了保证各变量在通过粗、细网格边界时满足连续性，粗、细网格的密度分布函数在碰撞后必须满足式 （4）、式 （5）。

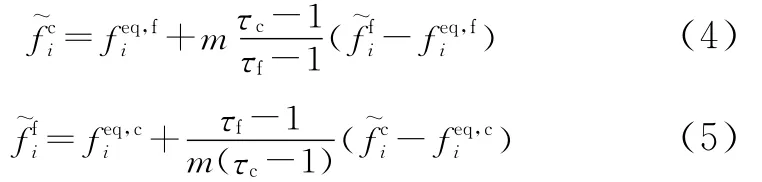
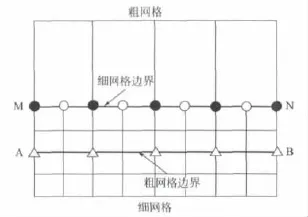
图1 粗、细网格边界结构图

从图中可以看出，粗网格与细网格在边界上互相交错。值得注意的是，在细网格边界MN上，黑点标记的格子点是没有原始信息的，由白点标记的格子通过采用3次样条插值的空间差分得到式（6）。

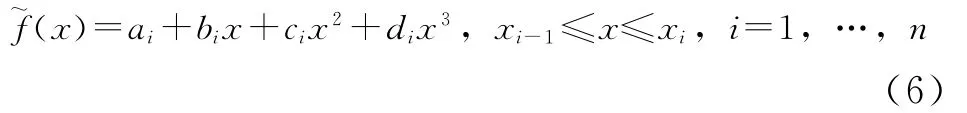
想要进行合理准确的模拟计算，粗、细网格的梳理速度必须相同，也就是说细网格进行m步梳理，粗网格只进行一步梳理，因此在细网格边界MN上需要用时间插值方法从而得出细网格在f（t（n＋1／m），MN）时的值。同样我们采用三点拉格朗日插值法得到式 （7）。

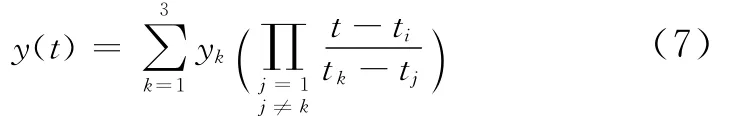
对于速度场与温度场的模拟，这些处理方法同样适用。

2 验证程序正确性

有自然对流换热的模拟较为复杂，对于自编程序是否能准确地研究含有自然对流的换热情况，需要验证程序的正确性。所以，可以通过模拟正方形空间内单热圆管自然对流这一经典算例并与前人结果进行对比以验证程序的正确性。作者模拟了瑞利数Ra＝1×104，Ra＝5×104和Ra＝1×1053种情况下热管表面平均努塞尔数、流线、等温线并与已有文献［13－15］进行了对比。

图2是热管在方形空间内的换热的多格子LBM模拟理论模型。正方形计算区域采用粗细两种网格，蓝色线代表粗网格，A－B－C－D是粗网格的内边界，红色线代表细网格，a－b－c－d是细网格的外边界。计算区域为2.5×2.5，划分成50×50的粗网格，步长Δxc＝Δyc为0.05以及内部50×50细网格步长Δxf＝Δyf为0.025，圆管直径为1。对于速度场，粗细网格计算区域中所有节点初始速度为0，四周均采用无滑移边界条件。对于温度场，圆管为恒壁温边界条件，量纲为1温度为1，四周采用恒壁温边界条件，量纲为1温度为0，流场中各节点的初始无量纲温度均为0。模型中热管的直径设为d，正方形区域边长定义为H，同时定义d／H为管径空间比，在这里取d／H＝0.4，为了方便与已有文献做比较，瑞利数Ra定义如式 （8），努塞尔数Nu定义如式（9）、式（10）。

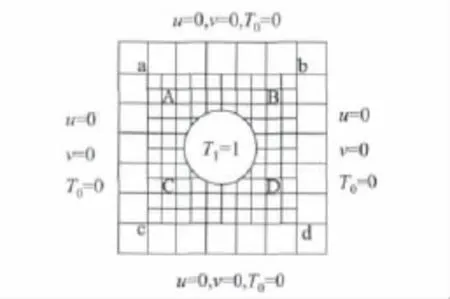
图2 单热管在方形空间内换热的多格子LBM模拟理论模型

瑞利数Ra

局部Nu数

表面平均Nu数

图3给出了Ra＝104情况下温度场和流场的模拟结果对比，图3（a）、（b）是Peng［12］等模拟的温度场和流场，图3（c）、（d）是王秋香等［14－15］采用均匀网格的模拟结果，图3（e）是采用多格子LBM的模拟结果，值得一提的是，计算时间相比均匀网格模拟节约了30%40%。

表1给出了平均努塞尔数Nu模拟结果的对比，本文模拟结果与Peng等［13］模拟结果的相对误差在0.2%2.6%，与王秋香等均匀网格的模拟结果误差在0.5%1.1%，相对误差在可接受范围内，充分说明了多格子LBM在大大节约计算时间的同时能够保证计算的准确性。

图3 温度场和流场的模拟结果对比

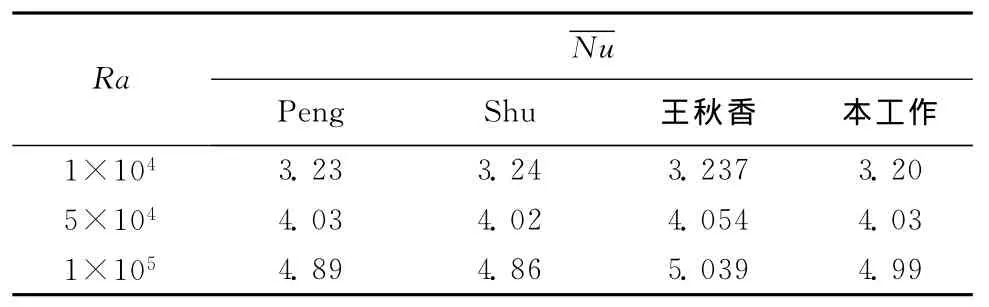
表1 平均努塞尔数Nu模拟结果的对比

3 冷热微圆管自然对流理论模型

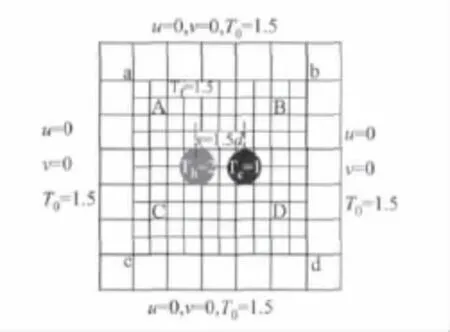
图4 冷热微圆管自然对流换热的多格子LBM模拟理论模型

图4是冷热微圆管自然对流换热的多格子LBM模拟理论模型。在模拟过程中设定雷诺数Re为0，研究纯自然对流情况下（具体是Ra＝103时的换热情况），冷热管中心连线与浮升力呈不同夹角对整体传热性能的影响。

在整个模拟计算中，冷热微圆管直径相同，量纲为1长度为1，计算区域20×20，划分成外围200×200的粗网格，步长Δxc＝Δyc为0.1，以及内部200×200细网格步长Δxf＝Δyf为0.05。对应于真实模型中：冷热微圆管外管径为1.0 mm，管间距为1.5d，也就是1.5 mm。速度场中，粗细网格计算区域中所有节点初始速度为0，四周采用无滑移边界条件。温度场中，冷热圆管为恒壁温边界条件，量纲为1，温度为1和 2，四周为恒壁温边界条件，量纲为1，温度为1.5，流场中各节点的初始温度均为量纲为1，温度1.5。值得注意的是，与验证程序不同，这里以圆管的直径d为特征尺寸来定义瑞利数Ra以及微管表面平均Nu。

4 模拟结果与分析

图5（a）给出了冷热管中心连线与浮升力垂直时的温度场流场的分布图。从图5（a）中可以看出，这种布管方式下，浮升力使被加热流体迅速上升，被冷却流体快速下沉，形成稳定的以冷热管中心连线为轴的上下对称的温度场分布。冷热管之间互有影响，热管的温度场向右倾斜 （冷管方向），冷管的温度场向左倾斜（热管方向）。

从流线分布可以看出，贴着热管壁面被加热的流体迅速上升，至上壁面分成两部分，一部分顺时针沿右壁面下行，至冷热管中心线水平位置后，流向冷管；而另一部分逆时针沿左壁下降，至冷热管中心水平位置后，流向热管。围绕冷管的流线与热管类似，但方向相反，基本上为中心对称。

图5（b）给出了冷热管中心连线与浮升力成45°的温度场流场分布图。从图5（b）中可以看出，这种布管方式下，浮升力使被加热流体迅速上升，被冷却流体快速下沉，形成稳定的以冷热管连线中心为原点的对称的温度场分布。相比冷热管中心连线与浮升力垂直布管方式，冷热流体分别在靠近底角点和顶角点聚集，换热效果略差于前者。

图5 冷热管不同布管方式的温度场流场

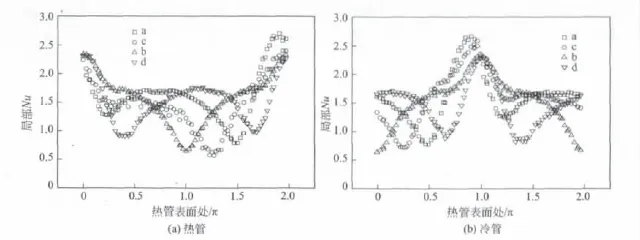
图6 不同布管方式下热管、冷管的局部Nu图

从流线分布可以看出，贴着热管壁面被加热的流体迅速上升，至上角点附近分成两股，一路继续顺时针沿右上壁面下行，在水平方向绕回构成回路。另一股逆时针方向流动沿左上壁面下行，水平方向绕回构成回路。而冷管周围被冷却的流体略偏左向下流动，在底角点分成两股，一路逆时针沿有下壁面上行，行至在水平方向受来流热流体阻碍，沿水平方向流回同时与热流体进行换热。另一路沿左下壁面顺时针上行，同样行至在水平方向受来流热流体阻碍，沿水平方向流回同时与热流体进行换热。这种布管方式被加热的流体与被冷却的流体之间没有进行充分的掺混，换热不充分。

图5（c）、图5（d）分别是冷热管中心连线与浮升力平行热上冷下以及热下冷上的温度场流场对比图。热管在上冷管在下时，形成以冷热管连线中心上下左右对称的温度场流场分布。浮升力使被加热的向上流动，被冷却的向下汇集。

热管在下冷管在上时，热管周围被加热的流体在浮升力作用下向上运动，但是在这过程中，受到正上方冷管的阻挡，必须要绕过冷管边缘才能继续上升。同样，冷管周围被冷却的流体在向下运动的过程中受到热管的阻碍，也必须绕过热管壁面才能继续下行。这就增大了被加热被冷却流体之间换热的阻力，使得整体换热效果较差。图6给出了不同布管方式下热管、冷管表面的局部Nu图。

表2给出了不同布管方式下冷热管表面平均Nu以及冷热管整体平均Nu的对比。结果表明，冷热管连线与浮升力垂直时冷热管的平均Nu最大，表示换热最好，热下冷上布管换热最差。

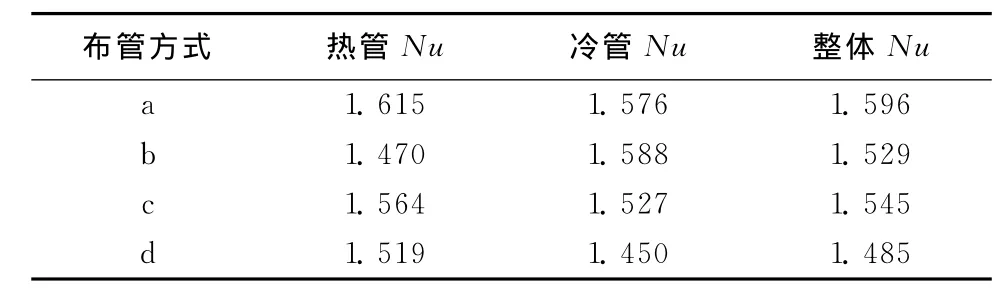
表2 不同布管方式下平均Nu对比

5 结 论

（1）冷热管中心连线与浮升力垂直的布管方式，浮升力使被加热流体迅速上升，被冷却流体快速下沉，形成稳定的以冷热管中心连线为轴的上下对称的温度场分布。冷热流体之间换热充分，整体换热效果最好。冷热管中心连线与浮升力成45°布管方式的温度场流场相比冷热管中心连线与浮升力垂直布管方式的温度场流场，冷热流体主要在靠近底角点和顶角点聚集，换热略差于前者。

（2）热管在上冷管在下的布管方式，形成以冷热管连线中心上下左右对称的温度场流场分布。浮升力使被加热流体向上流动，被冷却的流体向下汇集。冷热流体之间换热较好。

（3）热管在下冷管在上的布管方式，热管周围被加热的流体在浮升力作用下向上运动，在这过程中，受到正上方冷管的阻挡，必须要绕过冷管边缘才能继续上升。同样，冷管周围被冷却的流体在向下运动的过程中受到热管的阻碍，也必须绕过热管壁面才能继续下行。这就增大了被加热被冷却流体之间的换热阻力，使得整体换热效果最差。

符 号 说 明

m——空间步长比率，量纲为1

Δx——网格空间步长，量纲为1

τ——网格的松弛时间，量纲为1

v——流体的黏度，量纲为1

Ra——瑞利数，量纲为1

f——波尔兹曼密度分布函数

d／H——为管径空间比，量纲为1

β——体积膨胀系数，K－1

α——热扩散系数，m2／s

Nu——努塞尔数，量纲为1下角标

f——细网格

c——粗网格

［1］ 苏尚美，张亚男，成方园，等.微通道换热器的特性分析及其应用前景［J］.区域供热，2007，5：34－38.

［2］ 华贲，仵浩，刘二恒.基于火用经济评价的换热器最优传热温差化［J］.化工进展，2009，28（7）：1142－1146.

［3］ 支浩，汤慧萍，朱纪磊.换热器的研究发展现状 ［J］.化工进展，2009，28（s）：338－342.

［4］ 陆应生，陈墓玲，潘宁忠，等.强化传热元件与高效换热器研究进展［J］.化工进展，1998，1：46－48.

［5］ 戴传山，王秋香，孙平乐.污垢对微管换热器用于发电系统的影响［J］.化工进展，2009，28：371－375.

［6］Yan Y Y，Zu Y Q.Numerical simulation of heat transfer and fluid flow past a rotating isothermal cylinder－A LBM approach［J］.International Journal of Heat and MassTransfer，2008，51：2519－2536.

［7］Shu C，Liu N，Chew Y T.A novel immersed boundary velocity correction－lattice Boltzmann method and its application to simulate flow past a circular cylinder［J］.Journal of Computational Physics，2007，226：1607－1622.

［8］Lima E S，Silveira N A，Damasceno J.Numerical simulation of two－dimensional flows over a circular cylinder using the immersed boundary method［J］.Comput.Phys.，2003，189：351.

［9］Feng Z G，Michaelides E.The immersed boundary－lattice Bol－tzmann method for solving fluid－particles interaction problems［J］.Comput.Phys.，2004，195：602.

［10］Feng Z G，Michaelides E.Proteus：a direct forcing method in the simulations of particulate flows［J］.Comput.Phys.，2005，202：20.

［11］Sui Y，Chew Y T，Roy P，et al.A hybrid immersedboundary and multi－block lattice Boltzmann method for simulating fluid and moving－boundaries interactions［J］.Int.Numer.Meth.Fluids，2007，53：1727－1754.

［12］ 葛鑫.微管外流动换热的玻尔兹曼数值模拟研究 ［D］.天津：天津大学机械学院，2009.

［13］Peng Y，Shu C，Chew Y T.Lattice kinetic scheme for the incompressible viscous thermal flows on arbitrary meshes［J］.Physical Review，2004，E 69，016703.

［14］ 王秋香，戴传山，李琪.流向对管束外混合对流影响的数值模拟［J］.工程热物理学报，2011，32（7）：1221－1224.

［15］ 王秋香.微管换热器传热与流动性能的实验研究 ［D］.天津：天津大学机械学院，2010.