含死区和饱和的非线性系统PID 控制器设计

彭富明，方斌

(南京理工大学 自动化学院，江苏 南京210094)

0 引言

近30 年，控制技术获得飞速发展，如预测控制、自适应控制、滑模控制和智能控制等，但PID控制器仍然在各种实际控制系统中起着重要作用。PID 参数设计有很多实用有效的方法;近10年，关于PID 控制器三维稳定空间的研究取得一系列进展[1－6]，这些方法基本都是针对被控对象是线性的。然而，实际的系统不可避免存在一些非线性因素，尤其是控制器的输出普遍存在或多或少的死区和饱和现象。当死区和饱和现象不能忽略时，而所设计PID 控制器时，对这些非线性因素未能充分考虑，按线性对象镇定的系统其性能会明显下降甚至出现不稳定。文献[7 －9]运用线性矩阵不等式(LMI)，通过优化的方法，分析与设计抗饱和问题。文献[10]通过精心选择非线性增益函数，形成一个非线性PID 控制器。文献[11]提出了一种模糊PID 控制器的设计方法来提高含饱和特性系统的性能。文献[13]基于Lyapunov 理论提出一种饱和非线性PID 调节器，一些类似的方法见文献[14 －16].尽管这些方法各具特色，由于其对理论要求高、计算量大，对模型有一定要求等，并没有在实际控制工程得到广泛的应用。

基于将控制器的输出信号与被控对象的输入信号的差值作为反馈支路达到抑制饱和的目的，尽快消除饱和带来的系统性能恶化的思想，产生2 大类型的方法:传统的抗重置饱和(Anti－reset windup)和条件技术。这2 类方法由于设计简单，在实际系统中获得较好的应用。其设计过程主要有2 步:1)按线性对象设计PID 控制器本身，再根据经验设计反向计算的跟踪时间常数。一般情况下，它们能有效改善系统性能。但该方法并不总是有效抑制饱和现象，尤其当跟踪时间常数或PID 控制器本身设计不恰当时;2)当被控对象不稳定时，更无法保证系统稳定。由于非线性系统稳定性分析与设计在工程实践中较为困难，本文的基本想法是不改变原有的PID 控制器结构，提出一种PID 设计方法，克服了死区和饱和现象，并保证该非线性系统的稳定性;在系统有一个大的阶跃参考输入时，该系统仍然维持在一个大的稳定范围工作。虽然没有严格的理论证明，但其设计思路明确、方法简单，仿真实例表明，该方法适用于控制器离线设计，可满足实际应用要求。

1 问题表述

含死区和饱和的非线性系统如图1 所示。

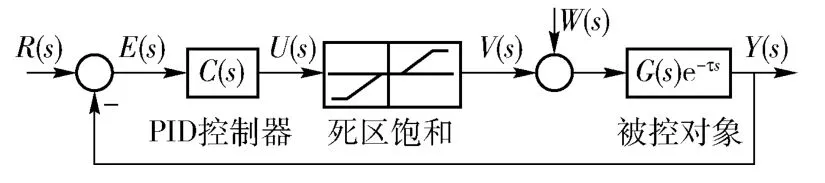
图1 含死区和饱和的非线性系统Fig.1 Nonlinear system with dead－zone and saturation

设控制对象为

式中:bi，aj(i =1，2，…，q，j =1，2，…，n1)分别为分子和分母多项式的系数，n1＞q，an1＞0，τ≥0.G(s)的逆函数为=1/G(s).

PID 控制器为

式中:KP、KI和KD分别为比例、积分和微分增益。

死区和饱和特性v 和其描述函数N(A)分别为

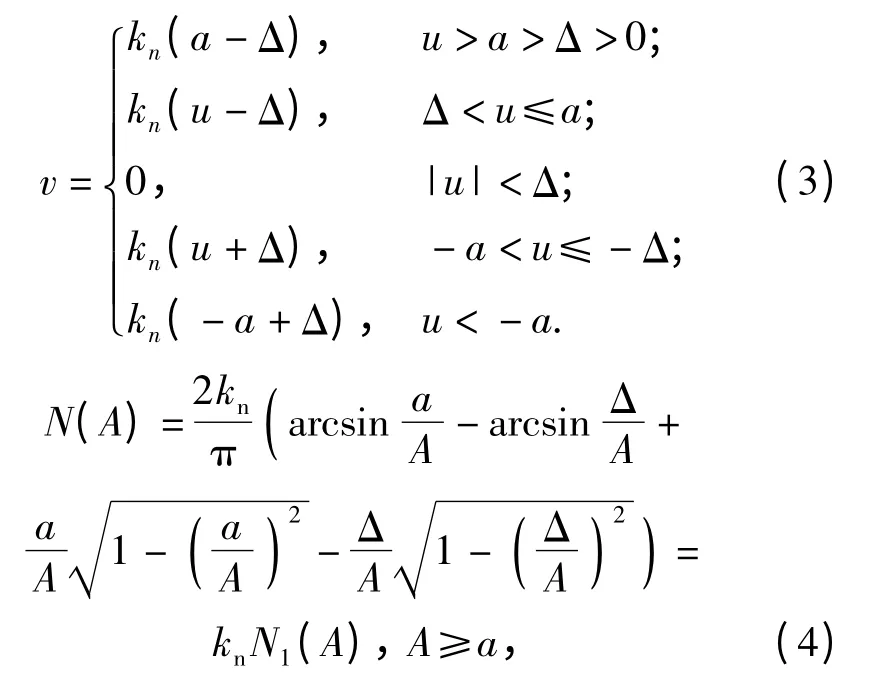
式中:A 为非线性环节正弦输入信号的幅值;kn为饱和部分的斜率。

非线性系统在PID 控制下的特征方程为

本文的目标是对死区和饱和的非线性系统，运用(5)式设计PID 控制器，在阶跃参考输入下使系统能保证具有较好的性能。

2 线性系统PID 参数稳定域方法

对于含时滞或不含时滞的线性系统PID 稳定域研究，其基本过程是首先确定比例增益KP稳定的范围;在该范围通过遍历增益KP，以确定KP为定值时相应的KD－KI平面上稳定区域。当图1 所示系统死区和饱和可以忽略时，相当于N(A)=kn，此时系统的闭环特征方程为

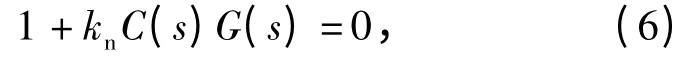
式中:s 的最高阶为n=n1+1.

(6)式可以改写的等价形式:

将s=jω 代入(7)式有:

由(8)式可分析确定增益KP的稳定范围[6]，(9)式可获得KD－KI平面一系列边界直线，进而运用逆时针规律可确定KD－KI平面上的稳定区域，具体方法见文献[5，17].确定含时滞或不含时滞的线性系统PID 稳定域的步骤如下:

2)在KP的稳定范围，取某一KP=，在复平面上作纵向直线，其横坐标为－，求出该直线与逆Nyquist 曲线)交点，这些交点对应的频率按从小到大顺序排列分别为ω0，ω1，…，ωl;ω0=0，j=1，2，…，l.在KD－KI平面，确定稳定范围的边界直线和KI=0.

4)在KP的稳定范围遍历KP，重复上述步骤，可获得含或不含时滞的线性系统PID 控制器参数稳定域的三维空间。

3 含死区饱和非线性系统的设计方法

众所周知运用描述函数分析和设计非线性系统是最经典的方法之一。为了有效延伸这种技术，利用(5)式计算死区和饱和非线性系统的PID 参数稳定域。最简单方法是使用等效的逆Nyquist 特性G(jω)/N(A)代替原逆Nyquist 曲线由于SIDF 模型依赖于非线性环节的正弦输入幅度A，而参考输入是阶跃函数时，输入幅度A 不是恒定的，可以选取适当的输入幅度集合{Ai}，i =0，1，2，…;(A0=a，Ai＜Ai+1)，该集合{Ai}尽可能覆盖非线性环节输入振幅的范围。通过上述处理，可直接用第3 节的方法计算出针对每个Ai的PID 参数稳定域Si.

本文所提出的方法是基于以下假设:当某一个确定的PID 控制器对不同的Ai都能使(5)式稳定，那么非线性系统本身也一定是稳定的。现在有2 种不同情况考虑。

3.1 开环稳定

开环稳定时，对图1所示的死区和饱和的非线性系统作如下分析:

1)如果PID 控制器输出长期处于饱和或死区状态，那么被控对象输入则为一个常数，闭环系统实际上一直处于开环状态。当被控对象是开环稳定的，则系统输出也是稳定的。

2)一般对于稳定的被控对象，如果Kp的稳定区间 是KP∈(KPi，KPi+1)，KP和KPi+1所 对 应 逆Nyquist 曲线上的2 点位于纵轴两侧，逆Nyquist 曲线必然随着Ai的增大逐步向外扩展;由于N(A0)＞N(A1)＞N(A2)＞…，通常有Si⊂Si+1和Si∩Si+1≠∅.虽然在集合Si+1－Si内设计PID参数，阶跃输入时闭环系统也能保证是稳定的，但此时控制器的输出一般都处于饱和状态。

此时，PID 控制器设计的基本步骤如下:

1)选取适当的输入幅度集合{Ai}，i =0，1，2，…，max ，使集合{Ai}尽可能覆盖非线性环节输入振幅的范围。虽没有具体的理论指导选择最大输入幅度Amax，但一般情况，振幅Amax越大，所设计的PID控制器更好地减弱饱和的影响。由于死区的存在，以及过大的Amax不仅造成计算量的增加，在实践中也是没有必要。一个简单的选择是2≤Amax/a≤4.

2)根据每一个新的等效逆Nyquist 曲线和第3 节所介绍方法，可以判断每个Ai所允许的比例增益稳定集合(范围)SKP，i.同时满足每个Ai所允许的比例增益稳定集合SKP=

3)在集合SKP内选择一个固定的KP∈SKP.根据第3 节所介绍方法，可以判断每个Ai所允许的微分和积分增益(KD，KI)稳定集合SKIKD，i.同时满足每个Ai所允许的微分和积分增益稳定集合SKIKD=

4)对图1 所示的死区和饱和的非线性系统PID 参数可根据KP∈SKP和(KD，KI)∈SKIKD选择。

3.2 开环不稳定

当开环不稳定时，对图1 所示的死区和饱和的非线性系统作如下分析:

1)当开环不稳定且系统处于死区或饱和状态时，闭环系统相当于开环，系统的输出也将是不稳定的;此时不仅要分析幅值Ai的变化对稳定域的影响，还要分析Δ=0 时的影响。

2)一般对于不稳定的被控对象，如果KP的稳定区间是KP∈(KPi，KPi+1)，KPi和KPi+1所对应的逆Nyquist 曲线上2 点位于纵轴同一侧;当Amax较大时，通常有Si∩Si+1=∅;因此不能选择太大的Amax.

综上所述，针对开环不稳定的系统，仅采用PID控制器是不能达到稳定系统的要求。一个新的结构被提出如图2 所示。对参考输入阶跃信号进行预处理GP(s)=1/TPs+1;预处理器具有低通特性，可有效抑制参考输入的突变带来系统的剧烈波动，实现系统的软启动;可以非常有效地改善非线性环节的影响，并确保闭环系统稳定。

图2 开环不稳定的非线性系统控制Fig.2 Control of nonlinear system for open－loop unstability

此时，PID 控制器设计的基本步骤如下:

1)～4)与开环稳定时相同。但最大振幅Amax可适当小些，一般1 ＜Amax/a≤3.

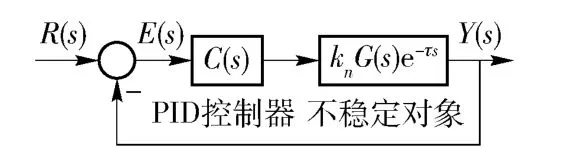
图3 具有相同PID 控制器的线性系统Fig.3 Linear system with the same PID controller

5)按前步骤4)所设计的PID 控制器应用于被控对象为knG(s)e－τs线性系统时，如图3 所示，该系统必然是稳定的。可从图3 获取该线性系统的调节时间ts，前置预过滤器的时间常数可以简单选择:TP＞(0.2 ～0.8)ts.

4 实例

例1 设被控制对象及死区和饱和特性参数为

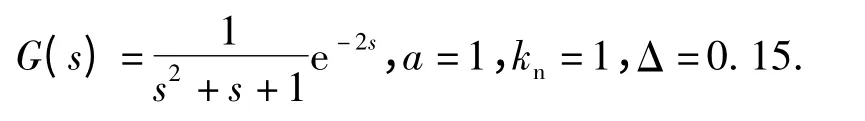
取振幅Ai=1，1.5，2，每个Ai所相应的比例增益稳定范围(集合)分别为:SKP，0=(－0.81，0.75)、SKP，1= (－ 0.654，0.608)和 SKP，2= (－ 0.51，0.478);则SKP=(－0.51，0.478).令KP=0.4，则每个Ai所相应的微分和积分增益稳定范围SKIKD，i，如图4 所示(图中坐标是后面2 个数据表示，即KP一定下的KD－KI图)。从图4 中选取4 个点P1、P2、P3和P4，4 个点所对应的PID 控制器参数(KP，KI，KD)分别为(0.4，0.2，0.3)、(0.4，0.5，0.6)、(0.4，0.5，0.8)和(0.4，0.4，1).4 种情况系统的单位阶跃响应如图5(a)所示;在t =50 s 加入脉冲扰动w(t)，其幅值为1、宽度为2 s.4 种情况PID 控制器的输出如图5(b)所示，可见交集SKIKD内点P1所对应的系统特性好于其他点，积分增益越小系统总体特性要好。

图4 例1 的微分和积分增益稳定范围Fig.4 The stable regions of differential and integral gains for Example 1

例2 设被控制对象及死区和饱和特性参数为

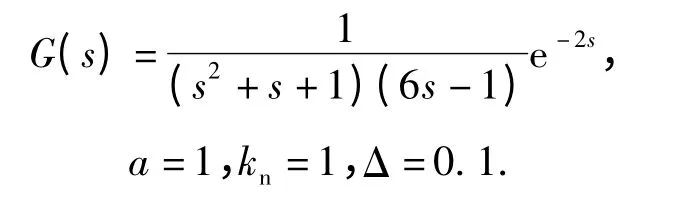
由于例2 为不稳定对象，需考虑完全线性条件下(a=∞，Δ=0)的稳定域，此时比例增益稳定范围为SKP，－1=(1，2.708).取振幅Ai=1，1.5，2，每个Ai所相应的比例增益稳定范围(集合)分别为:SKP，0=(0.873，2.364)，SKP，1= (0.696，1.885)，SKP，2=(0.545，1.477);则SKP=(1，1.477).令KP=1.4，则每个Ai所相应的微分和积分增益稳定范围SKIKD，i如图6 所示。从图6 中选取4 个点D1、D2、D3和D4，4 点所对应的PID 控制器参数(KP，KI，KD)分别为(1.4，0.05，1.5)、(1.4，0.05，2.5)、(1.4，0.1，2.7)和(1.4，0.1，3.7).4 种情况系统的单位阶跃响应如图7(a)所示，控制器的输出如图7(b)所示。可见交集SKIKD内点D1所对应系统特性好于其他点，积分增益越小系统总体特性要好。值得注意的是，即使是在交集SKIKD内选点，当所选取的点其积分增益较大时(靠近线A0时，见图6)，闭环系统将会不稳定;另外，当死区Δ 较大时，比例增益相应要增大。

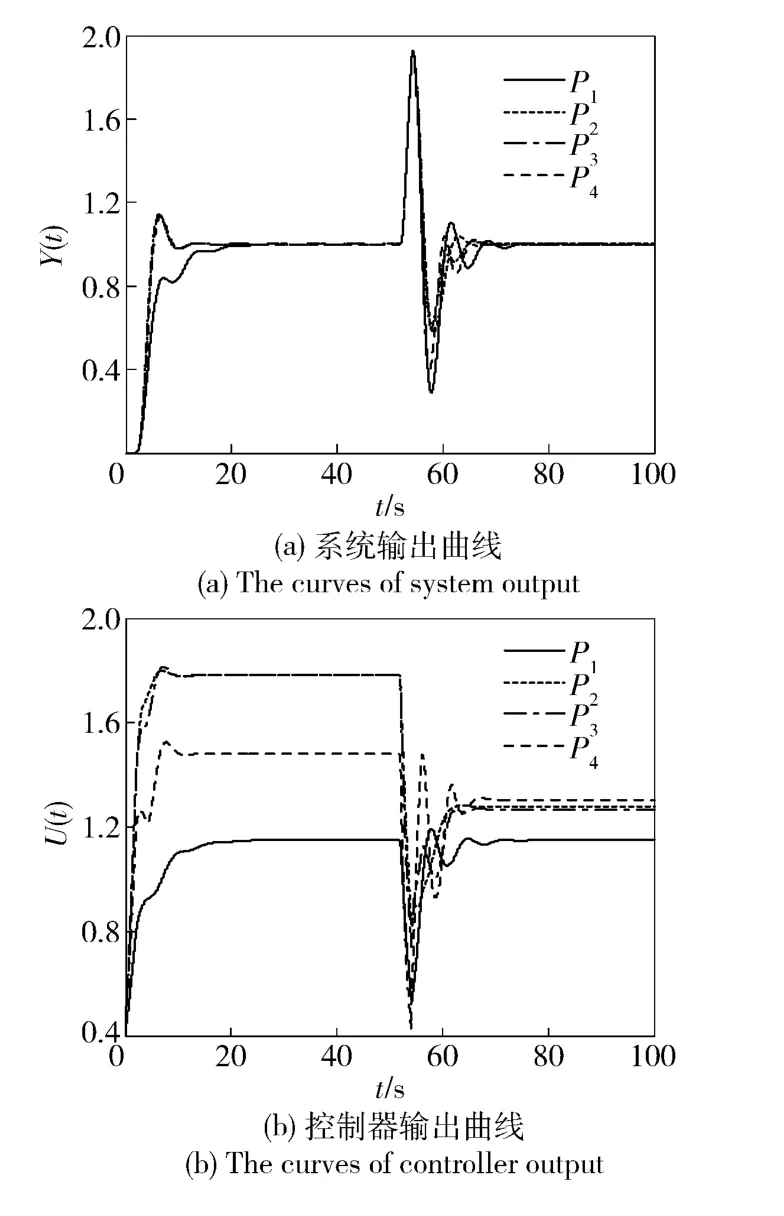
图5 开环稳定时系统阶跃阶跃响应和控制器输出Fig.5 System step response and controller output for open－loop stability

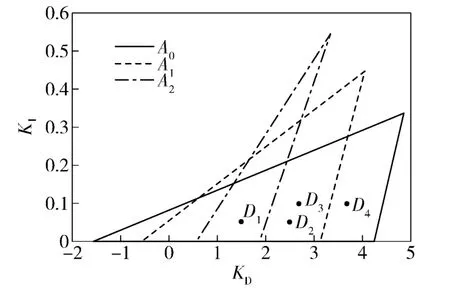
图6 例2 的微分和积分增益稳定范围Fig.6 The stable regions of differential and integral gains of Example 2

图7 开环不稳定时系统阶跃响应和控制器输出Fig.7 System step response and controller output for open－loop unstability

无论开环是稳定或不稳定的对象，在稳定域交集内选取较小的积分增益，控制系统性能就越好。对于开环稳定的对象，也可以对参考输入进行预处理，更好地改善设定值变化对系统性能的影响。对于开环不稳定的对象，所容许设定的PID 控制器参数集要小于文中的稳定域交集，且其抗扰动能力不强。为进一步提高稳定域交集的可行性，可以加入的相位裕度约束e－jγ(10°≤γ≤60°)，使所设计的PID 控制器具有更好的性能，此时新的等效逆Nyquist 曲线为如当γ =30°时，例1 的SKP=(－0.44，0.4476).取KP=0.4 时，则每个Ai=1、1.5、2 所相应的微分和积分增益稳定范围SKIKD，i如图8 所示;图8 中，细线为γ =0°(既为图4)，粗线为γ=30°情况。从图8 可见，只有P1点落入粗线所构成的区域交集SKIKD内。因而，加入相位裕度约束e－jγ，可使所设计的PID 控制器具有更好的性能。

5 结论

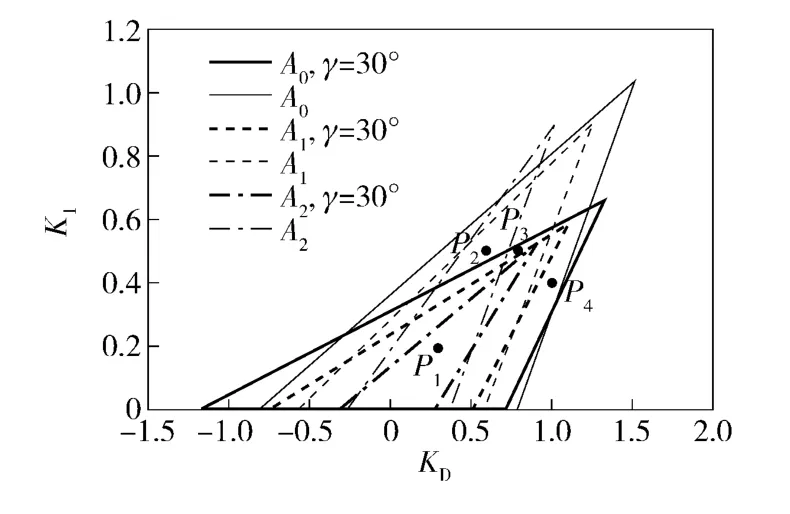
图8 γ=30°时例1 的微分和积分增益稳定范围Fig.8 The stable regions of differential and integral gains of Example 1 for γ=30°

本文研究含死区饱和特性系统的PID 控制器设计，并提出了一种设计方法。它可以减轻非线性对系统的影响。基于非线性环节的描述函数模型，一种新的等效逆Nyquist 曲线被提出。对于开环稳定的对象，PID 控制器参数的选取，可直接从不同的幅值Ai条件下参数稳定域的交集中获得。对于开环不稳定的对象，首先对阶跃参考输入进行预处理，并提供预过滤器时间常数的选取方法，PID 控制器的设计与开环稳定时相同，但开环不稳定时，系统抗干扰的能力较弱，在交集中积分增益较大的点仍可能不稳定的，所选点应尽量远离积分增益较大的边界线。本文提出的方法可以扩展到其他含硬非线性环节的系统。

References)

[1]Keel L H，Bhattacharyya S P.Controller synthesis free of analytical models:three term controllers[J].IEEE Transactions on Automatic Control，2008，53(6):1353 － 1369.

[2]Bajcinca N.Design of robust PID controllers using decoupling at singular frequencies[J].Automatica，2006，42(11):1943 －1949.

[3]Ho M T，Datta A，Bhattacharyya S P.Generalizations of the Hermite－Biehler theorem:the complex case[J].Linear Algebra and Its Applications，2000，320(1 －3):23 －26.

[4]Ackermann J，Kaesbauer D.Stable polyhedra in parameter space[J].Automatica，2003，39(5):937 －943.

[5]方斌.时滞系统PID 控制器参数稳定域的实现[J].电子科技大学学报，2011，40(3):411 －417.FANG Bin.Realization of PID controller parameter stable regions for time delay systems[J].Journal of University of Electronic Science and Technology of China，2011，40(3):411 － 417.(in Chinese)

[6]方斌.时滞系统PID 控制器增益的稳定范围研究[J].信息与控制，2009，38(5):546 －551.FANG Bin.On gain stabilizing regions of PID controller for time delay systems[J].Information and Control，2009，38(5):546 －551.(in Chinese)

[7]Grimm G，Hatfield J，Postlethwaite I，et al.Antiwindup for stable linear systems with input saturation:an LMI－based synthesis[J].IEEE Transactions on Automatic Control，2004，48(9):1509 －1525.

[8]Hu T，Teel A R，Zaccarian L.Anti－windup synthesis for linear control systems with input saturation:achieving regional，nonlinear performance[J].Automatica，2008，44(2):512 －519.

[9]Sajjadi－Kia S，Jabbari F.Scheduled static anti－windup augmentation synthesis for open－loop stable plants[C]∥American Control Conference (ACC)，2010.Baltimore:IEEE，2010:6751 －6756.

[10]Isayed B M，Hawwa M A.A nonlinear PID control scheme for hard disk drive servo systems[C]∥MED'07.Mediterranean Conference on Control ＆ Automation.Athens:IEEE，2007:1 －6.

[11]Huang Y，Yasunobu S.A general practical design method for fuzzy PID control from conventional PID control[C]∥The 9th IEEE International Conference on Fuzzy Systems.Texas:IEEE，2000:969 －972.

[12]Mhaskar P，El－Farra N H，Christodes P D.A method for PID controller tuning using nonlinear control techniques[C]∥Proceeding of the 2004 American Control Conference.Massachusetts:IEEE，2004:2925 －2930.

[13]Santibanez V，Kelly R，Zavala－Rio A，et al.A new saturated nonlinear PID global regulator for robot manipulators[C]∥Proceeding of the 17th IFAC Word Congress.Korea:IFAC，2008:11690 －11695.

[14]Zavala－Rio A，Santibanez V.Simple extensions of the PD－withgravity－compensation control law for robot manipulators with bounded inputs[J].IEEE Transactions on Control Systems Technology，2006，14(5):958 －965.

[15]Zavala－Rio A，Santibanez V.A natural saturating extension of the PD with desired gravity compensation control law for robot manipulators with bounded inputs[J].IEEE Transactions on Robotics，2007，23(2):386 －391.

[16]Alvarez－Ramirez J，Santibanez V，Campa R.Stability of robot manipulators under saturated PID compensation[J].IEEE Transactions on Control Systems Technology，2008，16(6):1333 －1341.

[17]Fang B.New approach to the realization of PID controller parameter stable regions[C]∥IEEE International Conference on Computer Science and Automation Engineering.Shanghai:IEEE，2011:627 －631.