Radon 变换对短模糊尺度下匀速直线运动模糊参数的准确估计
2013-02-28段若颖谌德荣蒋玉萍关咏梅高翔霄
段若颖,谌德荣,蒋玉萍,关咏梅,高翔霄
(1.北京理工大学 机电工程与控制国家重点实验室,北京100081;2.北京宇航系统工程研究所,北京100076)
0 引言
随着毫米波技术、红外技术、激光技术、微电子集成以及各种传感器技术向常规弹药的广泛渗入,智能弹药作为高技术兵器时代的常规弹药,具有信息感知与处理、推理判断与决策、执行某种动作与任务等功能,已经成为一个重要的发展方向[1-2]。精确打击目标能力是衡量智能弹药作战能力的重要标识之一[3],因而准确识别目标是实现预想打击效果的根本。然而当导弹与安装在其上的相机进行高速运动时,由于场景能量在成像平面上非正常累积,则产生运动模糊图像,导致了目标信息的模糊。为了获得符合要求的高品质目标图像,需要对运动模糊图像进行复原。经典的图像复原方法都是以图像退化的点扩散函数(PSF)为基础,在PSF 未知的情况下,需要对PSF 的重要模糊参数进行预估。因此,对模糊参数进行精确估计具有重要意义。
在实际过程中,弹载相机与目标之间的相对运动复杂。由于匀速直线运动造成的模糊图像最具有一般性,而变速、非直线运动在测量结果误差允许范围内均可被视为或分解为分段匀速直线运动,因此匀速直线运动模糊图像的模糊参数估计成为研究的热点,而短模糊尺度下的参数估计又成为研究的难点。文献[4 -6]基于运动模糊图像频谱特性,分别利用Hough 变换、Radon 算法、相关系数法来获得运动模糊参数,但是这些文献均只涉及短模糊尺度大于10 个像素的情况。文献[7]利用Hough 变换检测模糊方向,再用模糊方向上的Radon 变换曲线波谷位置差进行曲线拟合检测模糊尺度,仿真结果表明文中算法可适用于模糊尺度大于7 个像素的情况,但算法复杂,计算量大。文献[8]涉及到了模糊尺度较小时的模糊参数检测,但是仿真结果证明该方法当对图像进行5 个像素退化时,模糊尺度的检测误差增大到1.31 个像素。现有的运动模糊参数估计算法在低模糊尺度下均表现出低测量精度。
本文针对短模糊尺度下的运动模糊参数准确估计问题,提出了基于Radon 变换检测明暗相间投影线的方法,该方法简单有效,且参数估计准确。
1 运动模糊的频谱特征分析
设模糊图像g(x,y)由输入图像f(x,y)做匀速直线运动造成,则模糊后图像可表示为

式中:x0(t)为景物在x 方向上的运动分量;y0(t)为景物在y 方向上的运动分量;n(x,y)为加性噪声,T 为曝光时间。
假设图像未受噪声污染,即n(x,y)= 0.对g(x,y)进行傅里叶变换得
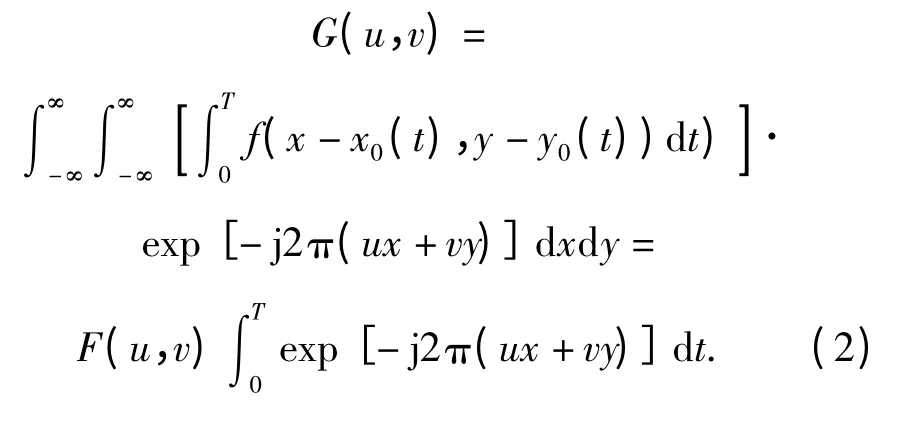
由于未受噪声的图像退化模型频域表达式为

式中:G(u,v)和F(u,v)分别为g(x,y)和f(x,y)的频域形式;H(u,v)为PSF 的频域表达式。根据(2)式和(3)式得

若图像在x 方向上的总位移量为a,在y 方向上的总位移量为b,则运动速率x0(t)= at/T,y0(t)=bt/T,则(4)式可变换为
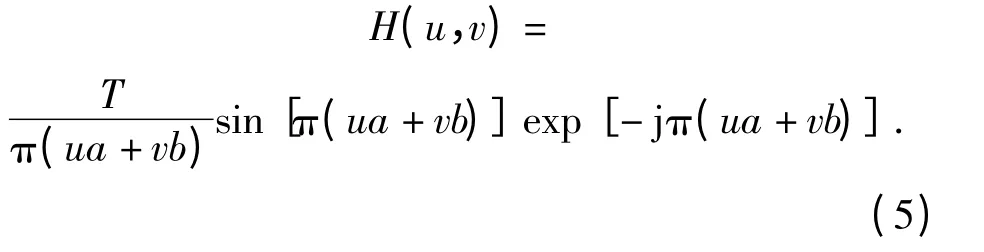
假设图像尺寸为N ×M(图像在计算机上存储为离散形式),则(5)式可表示为离散形式,对其求傅里叶变换得:
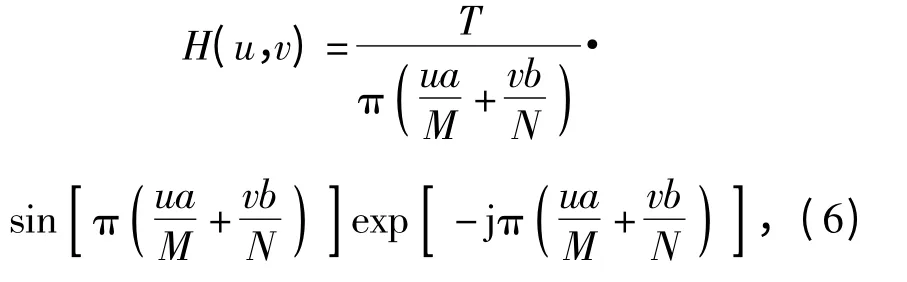
式中:u 取值为0 ~(M-1);v 取值为0 ~(N-1).
求(3)式模值,再与(6)式联立,得

式中:|H(u,v)|当(ua/M +vb/N)=0 时取得最大值T,此时G(u,v)显示为中心亮条纹;当(ua/M +vb/N)为其他整数时,G(u,v)= H(u,v)=0,此时G(u,v)显示为黑色条纹。如果M,N 为素数,虽然u,v在各自取值范围内无法令(ua/M+vb/N)为非零整数,但对于一般图像其频谱图依然会呈现规则的明暗条纹状,这是由于sinπ(ua/M+vb/N)为周期函数,它在自己的前后2.5 周期内呈现明显的递减和递增特性,从而也形成规则的明暗条纹[8]。
2 匀速直线运动模糊图像的参数估计
2.1 Radon 变换
Radon 变换可在任意维空间定义,而且定义也存在多种形式。对于二维函数f(x,y),Radon 变换计算它在某一指定角度方向上的投影变换,即在确定方向上的线积分。对图像而言,Radon 变换反映了图像在不同方向上的投影的性质。Radon 变换的二维表达式[5]为

直线l 的方程为
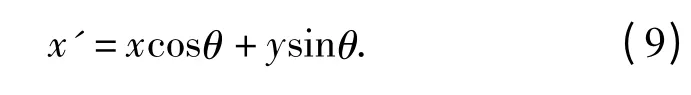
针对一幅图像,Radon 的几何意义是函数f(x,y)在θ 角度上,x'取遍所有值时,就得到其在θ 方向上的投影;再改变θ 值,就可以得到图像在不同方向上的投影。
2.2 运动模糊方向估计
基于匀速直线运动模糊图像的频谱特性,对(7)式取对数,目的在于对|G(u,v)|进行灰度级压缩,使得图像条纹更加清晰,则
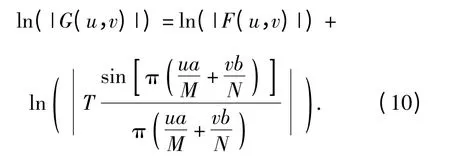
由于Radon 变换可以反映图像在不同方向上的投影性质,因此,可以通过研究频谱图在垂直于条纹方向时投影的特性,获得条纹方向。为表示方便,令M(u,v)=ln(G(u,v)),设M(u,v)中条纹倾斜角为α,则M(u,v)在方向的投影表达式为
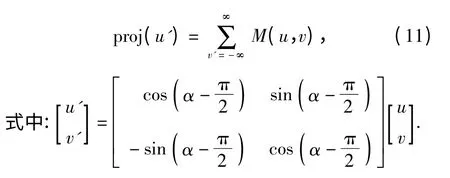

图1 匀速直线运动模糊图像频谱图及其投影图Fig.1 Spectrogram and its projected image of uniform velocity rectilinear motion blur
因此,在M(u,v)的Radon 变换图中获取proj(u'),proj(u')对应角度的垂直方向即为条纹倾斜角α.
分辨率为N ×M 的运动模糊图像,其频谱图条纹倾斜角α 与运动模糊方向ψ 的关系可表示为由此,运动模糊方向可被检测出。

2.3 运动模糊长度估计
根据点到直线的距离公式,中心点(0,0)到暗条纹(ua/M+vb/N)=1 的距离
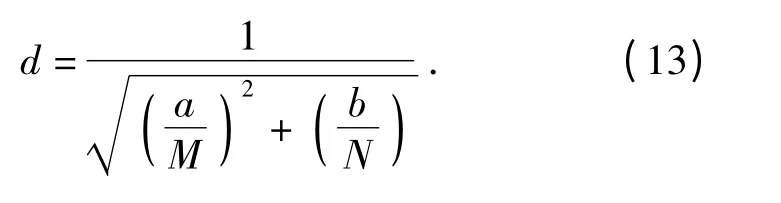
由对称性,图像中心2 个暗条纹之间的间距为D=2d,设模糊长度为l,则a = lcosψ,b = lsinψ,令M=σN,得

则由(11)式可得模糊长度
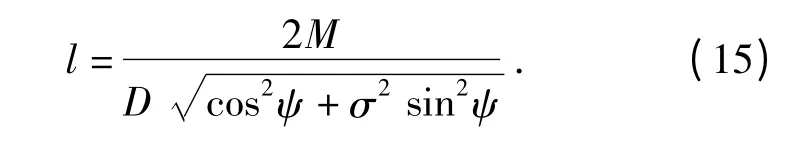
3 算法仿真与分析
当运动模糊图像的模糊尺度较小时,整幅频谱图中可供Radon 变换使用的暗条纹数目很少,此时的运动模糊参数估计误差高于长模糊尺度情况。因此,文中在不同模糊方向下,仅对分辨率为512 像素×512 像素的Lena 图像做模糊尺度分别为5 ~10 的退化,验证算法的有效性。图2 和图3 为仿真实验结果,图2 中横坐标为Lena 图像的真实退化模糊方向,纵坐标为文中提出算法对模糊方向检测的绝对误差,图中不同曲线代表不同模糊尺度退化后对模糊方向的检测误差。图3 横坐标为Lena 图像的真实退化模糊方向,纵坐标为文中提出算法对模糊尺度检测的绝对误差,图中不同曲线代表不同模糊尺度退化后对模糊尺度的检测误差。

图2 模糊方向检测误差曲线图Fig.2 Measurement error in blurred direction
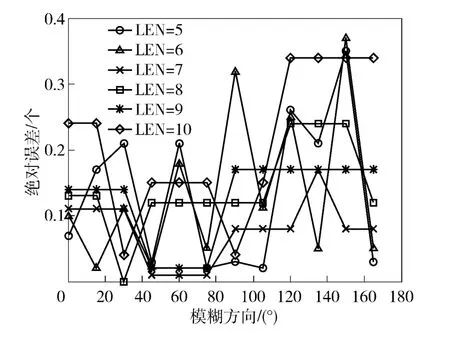
图3 模糊尺度检测误差曲线图Fig.3 Measurement extent in blurred direction
从图2 和图3 可以看出:1)在短模糊尺度下(模糊尺度为5 ~10),算法整体上是有效的。在运动模糊方向方面,当运动模糊图像的模糊尺度大于5 时,估计误差小于1°,当运动模糊图像的模糊尺度为5 时,估计误差上升至5°;在运动模糊尺度方面,估计误差小于0.5 个像素。2)在短模糊尺度下,当模糊方向为0°和90°时,估计误差最小。这是由于运动模糊图像频谱图中心的十字亮线使得0°和90°的模糊方向更易于其他方向检测。
4 结论
为提高短模糊尺度下的运动模糊参数精度,提出了一种改进的基于Radon 变换的运动模糊参数估计算法。从傅里叶变换角度,分析了匀速直线运动模糊情况下的点扩展函数的零点特性;从Radon变换角度,论证了匀速直线运动频谱图在垂直于条纹方向下Radon 变换时为明暗投影线的特性;根据理论和实验结果提出了运动模糊方向和运动模糊尺度的估计算法。从仿真验证结果可以看出,该方法原理简单,计算方便,可以有效估计匀速直线运动模糊图像的运动模糊参数,估计精度优于现有研究。
本文的研究基于理想状态,未考虑噪声污染的情况,因此,该算法的抗噪性成为未来研究的主要方向。
References)
[1]王颂康.灵巧弹药的发展和爆炸成形弹丸战斗部[J].兵工学报:弹箭分册,1991,(2):80 -81.WANG Song-kang.Smart munition development and explosively formed penetrator warhead[J].Acta Armamentarii:Projectiles and Rockets,1991,(2):80 -81.(in Chinese)
[2]王昊宇,徐学强,房玉军.网络化协同打击弹药技术[J].兵工学报,2010,31(增刊2):136 -137.WANG Hao-yu,XU Xue-qiang,FANG Yu-jun.Network cooperative attack ammunition technology[J].Acta Armamentarii,2010,31(S2):136 -137.(in Chinese)
[3]李勇,付庆红,田大新.陆军精确化火力支援武器装备体系及发展[J].兵工学报,2010,31(增刊2):112 -113.LI Yong,FU Qing-hong,TIAN Da-xin.Armament system and development of army’s precise firepower support weapon[J].Acta Armamentarii,2010,31(S2):112 -113.(in Chinese)
[4]张变莲.一种基于Hough 变换的运动模糊图像复原方法[J].科学技术与工程,2010,10(28):7018 -7021.ZHANG Bian-lian.A recovering approach for motion blur based on Hough transformation[J].Science Technology and Engineering,2010,10(28):7018 -7021.(in Chinese)
[5]Moghaddam M E,Jamzad M.Finding point spread function of motion blur using radon transformation and modeling the motion length[C]∥Proceedings of the Fourth IEEE International Symposium on Signal Processing and Information Technology.Rome:IEEE,2004:314 -317.
[6]Tanaka M,Yoneji K,Okutomi M.Motion blur parameter identification from a linearly blurred image[C]∥International Conference on Consumer Electronics,Digest of Technical Papers.Las Vegas:IEEE,2007:l-2.
[7]范海菊,冯乃勤.短模糊尺度下运动模糊参数的频域识别方法[J].计算机工程与设计,2011,32(1):244 -247.FAN Hai-ju,FENG Nai-qin.Frequency domain approach to motion blurred parameters identification at short blurred extent[J].Computer Engineering and Design,2011,32(1):244 -247.(in Chinese)
[8]李宇成,贾宝华,杨光明.运动模糊图像的参数估计与恢复[J].计算机工程与设计,2010,31(19):4247 -4249.LI Yu-cheng,JIA Bao-hua,YANG Guang-ming.Blur parameter identification and restoration of motion blurred image[J].Computer Engineering and Design,2010,31(19):4247 - 4249.(in Chinese)
