基于P—集合的传播模型

陈丽萍

摘 要：本文将具有动态特性的P-集合理论引入到传播学中来，利用P-集合建立传播过程的数学模型。阐述了信息X传递过程中的动态特点和属性特征，可以用一个动态集合对 来描述信息传播过程中接收者对信息理解的近似度，即发现当信息发生精确传递时动态集合对 回到原始信息X，没有发生精确传递时，接收者对信息的理解接近原始信息，即 是 的内P-集合， 具有向内收缩的动态特性； 是 的外P-集合， 具有向外扩张的动态特性。引入函数变换f和信息的属性特征α，进一步说明信息传播过程的实质。最后，通过实例说明模型的有效性。

关键词：P-集合；传播模型；数学模型

中图分类号：G20 文献标识码：A 文章编号：1672-8122（2013）02-0119-02

申农和韦弗是传播数学理论中最基本的传播模式，在此基础上的许多研究工作展开。随着信息理论的发展，学者们将粗糙集理论、拓扑学等理论用于研究传播学，建立了信息的粗传递模型[1～2]、信息传播的拓扑特征[3～5]等，丰富了传播理论，促进了传播学的发展。无论是利用粗糙集理论，还是拓扑学的知识，它们都将信息集合做为一个静态集合，研究信息传递过程中的不确定性。实际上，信息从P1传递到P2时，信息可能由于双方的知识的不同，使得原始信息到达P2时，原始信息X在P2那里变成X′了，即，原始信息X传播一次后，到达P2后发生了变化，这种变化说明信息的传播过程中的动态特性。如何从信息的动态特性来看传播过程？如何用数学模型来描述这一动态的传递过程？这一动态传递又有怎样的结构特点？本文将具有动态特性的P-集合理论引入到传播学中来，利用P-集合建立传播过程的数学模型。

一、P-集合的基本概念[6～7]

P-集合是一个动态集合对，普通集合是这一集合对的一个特例，P-集合具有动态特性。

约定X是有论域U上的普通有限非空集合，U是有限元素论域，V是有限属性论域。

定义1给定信息 ，称 是X生成的内P-集合，简称 是内P-集合。

定义2 给定信息 ，称 是X生成的外P-集合，简称 是外P-集合。

定义3由内P-集合 与外P-集合 构成的集合对，称作X生成的P-集合，简称P-集合，有限普通集合X称作逆P-集合 的基础集合。

二、基于P-集合的传播模型

申农的信息传播模型做为传播学的基本模型，描述了信息传播的过程。编码规则和解码规则的重叠度分为三种情况：1.P1编码知识和与P2的解码规则完全一致，则完全不能解码；2.P1的编码知识和与P2的解码规则部分重叠，则部分解码；3.P2的解码知识≥P1的编码知识，则完全解码。

根据的申农的传播模型可以做如下约定：设信息X是由n个信息元素构成的集合，即 ，该信息的属性是 。这三种情况在数学中我们可以理解为信息到达P2后具有动态特性了，或者P2对信息的理解是近似的，这种近似程度我们可以用一个动态集合对表示。而具有这种动态特性的集合对就是P-集合。

信息X由P1编码后通过渠道传递给P2，P2对作息编码之后便获得了原始信息。，由于P1的编码过程、P2的解码过程会对信息的理解有偏差，此时信息X到达P2时可能有如下三种情况：1.信息X发生精确传递，这也是信息传递的最理想情况；2.信息X到达P2时，可能由于P1编码或者P2的解码有偏差，导致P2对信息X和理解是不精确的，即对信息的理解是近似接近的，这种近似度可以用一个动态集合对 来描述，即 接近于原始信息；3.P2信息的理解完全是不准确的。

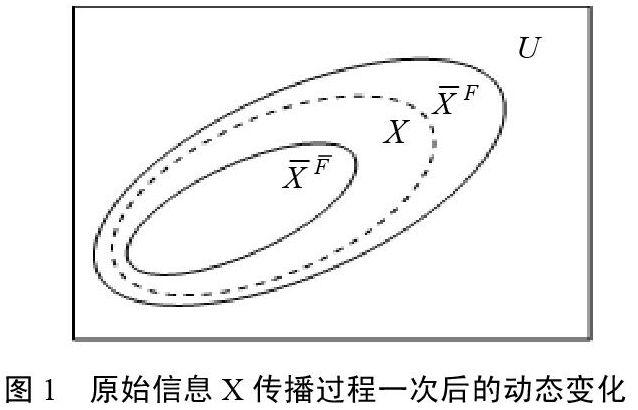
图1 原始信息X传播过程一次后的动态变化

图1中的虚线指原始信息 ，由图1可以看出， 是 的内P-集合， 具有向内收缩的动态特性； 是 的外P-集合， 具有向外扩张的动态特性。当信息 由P1通过渠道传递到P2时，P2对信息X的理解是不全面的，可以表示为 ，当P2对信息X理解准确时，此时动态信息集合对 回到 。

基于对信息X的重新定义，我们可以进一步理解为当信息X由P1通过渠道传递到P2时，由于P1对信息的编码与P2对信息的解码过程，从数学的角度可以理解为一次函数变换，记为f，设F是变换集合，且 。对 把某一信息元素u变成 。变换f称作元素迁移，此时的新元素u迁移是将新的元素迁入信息集合 中，此时信息 变为 ；反之，当 中元素迁出，即发生变换 ，且 。对 把 变成 ，即把某一信息元素 迁出信息集合 ，使得信息 变为 。当 时，信息 发生精确传递，此时动态集合对 回到基础集合 。

由以上元素迁移过程可知，随着元素的迁入、迁出，使得信息X中的元素个数发生变化，同时集合X信息属性发生改变。信息X发生一次传递，到达P2时具有动态结构 ，此时其属性集合也会发生变化。我们常说的“添油加醋”，可以理解为使原始信息元素增加的，同时原始信息的属性范围缩小；而“粗枝大叶”一词述描传递过程时，可以理解为使原始信息元素减少，同时原始信息属性范围扩大。信息 ，其属性集合是 。当信息由P1传递到P2后，信息 变成 ，其属性集合变为 ， ， 。信息发生一次传递后，由于原始信息元素个数的减少，使得该信息的属性范围扩大，即新的属性 通过一个函数变换 后进入属性集合，变为新的属性集合 。同样地，当信息由P1传递到P2后，信息 变成 ，其属性集合变为 ， ， 。信息发生一次传递后，由于原始信息元素个数的增加，使得该信息的属性范围缩小，即新的属性 通过一个函数变换 后迁出属性集合，变为新的属性集合 。

三、实例分析

例如一条信息X：“北京时间2011年3月11日13时46分日本东北部宫城县以东太平洋海域发生里氏9.0级地震，震源深度为10公里。”依据此信息我们可以将信息写成集合的形式： ={北京时间，2011年3月11日13时46分，日本东北部宫城县以东，太平洋海域，发生，里氏9.0级地震，震源深度，10公里}；信息 的属性集合 ={时间，地点，发生什么事}。

当信息 从甲方通过某一媒介传递到乙方时，乙方得到的信息为 ，即可以分以下情况讨论：

1.由于传递过程中信息元素的遗漏而使信息元素减少，扩大该信息的属性。例如由于甲对时差的忽略，传递信息为“2011年3月11日13时46分日本东北部宫城县以东太平洋海域发生里氏9.0级地震，震源深度为10公里。”那么乙得到信息是少了北京时间，信息传递到乙时，信息变为 ，信息元素 丢失，使得信息 的属性集合中的时间发生变化。由于乙无法确定是北京时间、还是伦敦时间、还是日本当地时间……，从而使信息到达乙后，属性集合中 发生变化，即时间属性扩大了。即乙得到的信息为 ，其属性集合为 ，这里的 较原来的时间属性 范围更大了， 。

2.由于传递过程中信息量的增加使信息元素的增加，缩小了该信息的属性的范畴。例如由于甲对信息X比较关注并知道更多关于此事件的信息，传递信息为“北京时间2011年3月11日13时46分日本东北部宫城县以东太平洋海域发生里氏9.0级地震，震源深度为10公里，13498人遇难，14734人失踪”。那么乙除了知道原始信息外，还了解到信息“13498人遇难，14734人失踪”，此时乙对信息属性中的 了解的更加确切。即传递到乙时，信息变为 ，信息元素 为新的信息元素，乙得到的信息更加具体，使得乙知道发生的事件更多，他会从此信息获知日本发生了地震且此次地震死伤人数很多，与原始信息中的属性 比较， 中隐含死伤可能严重可能不严重，而信息到达乙后的信息 ，其属性集合 范围会缩小，从而使我们对信息的解更加准确。即乙得到的信息为 ，其属性集合为 ，这里的 较原来的时间属性 范围缩小了， 。

3.信息发生准确传递，信息量没有增加也没有减少，此时信息 由甲传递乙时到没有发生变化，即 回到原始信息 。

将动态信息集合对 、其属性集合α和动态变换对 引入传播模型后，我们可以从P-集合理论来描述传播过程中的动态特性，而对P-集合的深入研究也为进一步理解传播理论提供理论支持。

参考文献：

[1] 刘纪芹，史开泉.基于粗糙集的信息粗传递[J].系统工程与电子枝术，2007（3）.

[2] 刘纪芹，韩建新.模糊信息粗传递模型及其应用[J].计算机工程与应用，2009（2）.

[3] 昝廷全.论传播的分类及其数学模型[J].中国传媒大学学报（自然科学版），2006（2）.

[4] 昝廷全，应思思.传播有效性原理的粗传递模型[J].中国传媒大学学报（自然科学版），2010（4）.

[5] 孙庆川，山石，兰田田.一个新的信息传播模型及其模拟[J].图书情报工作，2010（6）.

[6] 史开泉.P-集合[J].山东大学学报（理学版），2008（11）.

[7] 史开泉.P-集合与它的应用特性[J].计算机科学，2010（8）.