危险品配送中心选址及路线选择问题研究

乔联宝，朱华桂 （南京大学 工程管理学院，江苏 南京 210093）

QIAO Lian-bao,ZHU Hua-gui (School of Management and Engineering of Nanjing University,Nanjing 210093,China)

随着我国国民经济的快速发展，危险物品的社会需求量和供给量迅速增长，道路危险货物运输量也随之快速增长。目前，有超过3 300种物质属于危险品范畴。据估计，我国有害危险物品年产量约在6 000万吨以上，在世界范围内，有害危险物品年产生量约为30～40亿吨[1-2]。这些统计数据表明，如果对有害危险物品的存储、运输、使用等环节不采取系统而科学有效的管理措施的话，有害危险物品将会对社会和环境构成巨大的潜在威胁。

危险品需求量和事故危害程度的增加，使得政府部门和社会公众对它的重视程度也越来越高。危险品事故的严重性将会导致对危险品储存运输的研究更加深入，危险品的危险特性也将被纳入到危险品物流系统的决策环节中。但是企业关注的主要问题往往是如何选址、选线以使成本降低，而政府和居民则更加注重选址和运输带来的危险性以及服务能力的效果，这两个方面往往是互相矛盾的，如何在两者之间做到权衡，是解决问题的关键[3]。而目前国内针对这一问题的研究还比较少，所以还有待于进一步深入研究、探讨。

选址和配送实际上是密不可分的，选址是物流系统战略规划的重点，它决定了整个系统的模式、结构和形状，而且配送中心的建设也是一项耗资巨大的项目[4]。但是企业的物流成本却并非仅仅只有这些，一旦配送中心建立起来，企业要进行长期的物质配送，这部分费用会随着运输活动的进行而持续发生。如果将选址看作战略性决策的话，那么路径选择可以认为是战术性决策，而且选址会对路线的选择造成影响，所以，综合考虑两者的集成问题研究更具有现实意义，也更贴近现实情况。

但是由于选址问题 （LAP）和车辆路径选择问题 （VRP）本身都属于NP难题，这就为精确地求解两者的集成问题带来了巨大的困难。危险品作为一类特殊的物品，该类物质的选址和运输不仅要考虑一般物品所必须考虑的成本因素外，还需考虑它所带来的系统风险以及发生意外时对社会所造成的危害等。危险品本身的特殊性以及两类NP难题的集成使得对危险品选址和运输路线选择问题 （LRP）的研究相对较少，所以对此类问题的研究既是现实的迫切需要，也具有十分重要的理论意义[4]。

1 国内研究现状

国内关于选址问题的研究很多，但都主要集中在普通物流的选址研究方面，关于危险品的选址研究很少，而且也只是最近几年才刚刚开始。关于有危害物资的选址的研究，国内主要分为固体废弃物的填埋选址、垃圾填埋场的选址和有害物质填埋场的选址。

国内对LRP的研究起步较晚，直到汪寿阳等人第一次在国内提出LRP，并报道了关于这一领域有影响的研究成果后，才引起国内学术界对集成物流管理系统研究的重视，开展关于LRP的研究[5]。

郭晓峰等人最早研究了只考虑线性运输成本的单设施选址问题，所建的模型也假设运输车辆数目唯一，且车辆无容量限制，送货无时间窗口约束[6]。

随后，张静等人考虑了车辆的固定使用成本，以费用最小化为目标建立了车辆有容量限制的多车辆多设施的LRP数学模型[7]。

章海峰等研究了一类运输工具受物流网络节点最大单批处理能力及运输工具总运输能力双重能力约束的LRP问题[8]。

但是以上研究都没有涉及到关于危险品的选址或路线选择问题。而且，目前国内关于危险品选址或路线选择的文章也较少。王刊良等针对在有害危险品的运输网络中检查站设置的问题，以漏检有害危险品车辆的吨公里数最小化作为优化目标建立了评价检查站系统效率的模型[2]。

后来王刊良在有害物品的后勤管理方面，提出了有害危险物品管理中的风险表示与风险分析方法，有害危险物品运输过程的选线以及有害危险物品处理点 （如填埋场、焚烧厂）的选址模型[1]。

田绍军，张钦等通过建立危险品配送中心选址影响因素的层次分析评价模型，计算出各影响因素的权值，从而确定选址决策的主要影响因素[3]。

张敏等以路网的危险度瓶颈限制为切入点研究了一类危险品集成物流管理系统选址-选线问题，通过分析成本、风险和风险公平性等优化目标，建立了基于路网危险度瓶颈限制的危险品集成物流系统选址-选线的多目标模型，并给出了一种启发式算法[9]。

魏强通过把层次分析法 （AHP）应用于危险化学品储存、运营模式的优选决策上，从影响危险化学品储存、运营效率的安全性、经济性、社会性、技术性、政策性等决策指标进行综合考虑，制定了成本、安全、服务水平、可靠性、协调性和环保性决策准则[10]。

通过以上对国内外研究现状的分析可见，我国关于危险品配送中心选址-路线选择问题的研究还不够成熟，没有形成体系，很多的研究还不够深入，研究过程中考虑的因素也不够全面，方法也局限于定性的居多。目前，大部分研究都没有考虑危险品的运输过程对运输路径造成的危害以及选址对周围居民的影响，而多数研究只是考虑了成本问题，这与危险品物流的实际要求是不相符的，远远落后于危险品物流的实际发展进程，所以本文的研究不仅考虑选址和运输的总成本，还将考虑选址点对周围居民的影响以及危险品运输时对路网和路线周围居民造成的潜在危害。

2 危险品的选址—配送模型

（1）参数符号及变量含义

设：S=｛r|r=1,2,…,R ｝是R个候选配送中心集合；

D=｛i|i=R+1,…,R+N ｝是N个需求点集合；

M=S∪D是所有候选配送中心和需求点的集合；

V=｛vk|k=1,2,…,K ｝是从配送中心出发的K辆可用车集；

Dij表示节点i和节点j的距离；

Pij是在节点i和节点j之间路线影响范围内的居民数量；

drij为节点i和节点j之间路线影响下的居民中心离该路线的直线距离，并假定暴露在路线i和j下的居民数量与居民中心离该路线的直线距离成反比；

Rij为节点i和节点j之间路线发生交通事故的概率，它可以通过以往的统计资料获得；

c0为每两运输车的使用成本；

c1为单位距离的运输费用；

qj为每个周期内第j个需求点的需求量；

T为考虑的经营周期；

Q为运输车辆的最大装载量；

Hr为第r配送中心的最大容量；

Fr为第r个配送中心的固定建设成本；

Pr为配送中心r处的居民数量，选址风险与该处的居民数量成正比 （确定配送中心r处的居民数量时，可以规定一个有效的危害半径，只统计在该半径范围内居民数量）；

α为道路发生运输事故风险的经济转化因子，可以理解为每发生一次道路运输事故时的期望损失；

β为将暴露人口数量转化为经济指标的转化因子，可以理解为危险品对居民影响的社会成本；

Zr为0-1决策变量，若Zr取1，则在r处建造配送中心，否则，不在该处建造；

Xijk为0-1决策变量，若Xijk取1，则表示第k辆车从节点i到节点j，否则，第k辆车不从节点i到节点j；

Ui为辅助变量。

（2）模型假设及约束条件

假设1：各个配送中心的固定建造费用已知，并且具有容量限制，Fr为第r个配送中心的固定建造费用；Hr为第r个配送中心的最大容量。由于每个配送中心发出货物不超过其容量，所以有：

假设2：运输工具具有最大容量限制，但足以满足任意一个需求点的需求量。对于小件的物品配送，该假设显然是合理的，并且Q为运输车辆的最大容量 （在此，假定每个配送车辆的容量相同，但这并不是必须的）。由此产生的约束为：

假设3：配送中心和需求点的运输距离已知，并且每条运输路线的事故发生率已知。点i到点j的距离Dij一般可以按照两点之间的公路连线距离计算；两点之间的事故发生率Rij可由交通部门统计数据获得的。

假设4：各条路线附近的居民数量已知，距离按照居民中心点到路线的垂直距离计算且已知。一般只需统计各路线一定距离范围内的居民数量Pij，并可由人口普查数据获得，居民中心离路线的距离可按重心法等方法计算。

假设5：暴露的人口数量风险只受运输工具是否空载影响，危险事件概率风险固定不变。在现实情况下，暴露人口数量风险要受到运输工具所装载的危险品货物的数量的影响，例如，一辆满载炸药的运输车辆和一辆空载的运输车辆对道路以及周围居民的潜在危害显然是不同的，因此，考虑到危险物品运输过程中的风险大小与货物量正相关，所以更科学的方法是在运输过程中考虑运输工具所承载的危险物品量。同时，危险事件概率风险也要受出货时段的影响，在交通高峰期运输车辆通过道路的风险也较高，有时气候状况的因素也不能忽略。鉴于模型和计算的复杂性，本文并不作如此精细的考虑，只是假定运输工具非空载条件下，它们的影响是相同的；在空载情况下，运输工具不会对附近居民和道路产生潜在危害。所以，在运输工具从某一点返回配送中心时没有此两项风险的影响。

假设6：物品在各配送中心是单向流出 （delivery），并且各配送中心也不会相互配货，因此不必考虑运输车辆返回的情形。

假设7：没有硬时间窗口约束，在研究的时间内各需求点的需求量不变。假定需求点的需求量在各时期固定不变并不是必需的，只是为了简化计算。

假设8：决策目标要求在给定时期内总的成本和系统总风险最小，并且风险可以通过相应的转化因子α、β转化为经济指标，从而将多目标优化变为单一目标优化。为了保证每个需求点仅被一个车辆服务，从各个配送中心出发的所有车辆必定只有一个会访问该需求点，所以有以下约束条件：

为了保证每个节点由同一辆车进入，同一辆车驶出，有以下约束条件：

由于每一辆车最多只能从一个配送中心驶出，所以有：

为了使任意两个配送中心之间没有联系 （假设6），否则没有必要设立另一个配送中心，所以有[7]：

由于当一个配送中心建造时，则它必定至少会对1个对需求点进行配送，所以有：

另外只有当一个配送中心建造时，它才可能对需求点进行配送，所以有：

为了保证每条线路从一个配送中心开始，并且终止于该点，有以下约束[4,11]：

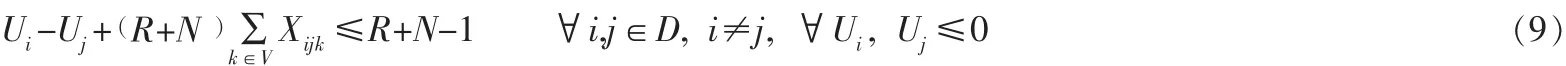
最后，由于决策变量ZrXijk都是0-1变量，所以有：

（3）危险品物流系统优化目标分析

成本：一般来说，系统优化都要考虑到成本因素，成本是影响物流系统设计的一个重要方面。在本文的物流配送系统规划中，这方面的成本通常包括配送中心的建设成本、运营成本、物品储运过程的储存与运输成本等。而危险品作为一类特殊的物品，有时还需考虑为了监督有害危险物品储运单位遵守管理条例所需要的管理成本 （如设置检查站、应急站）等等[1]。本文主要考虑配送中心设施选址的固定费用 （包括土地租赁费用、建设费用、维护费用等）、物品运输费用和车辆购置费用，并且在考虑的经营周期内将这三项成本之和最小化作为一个优化目标，有时鉴于考虑的时间跨度，往往需要根据货币的时间价值进行调整，但本文并不做这种考虑。在模型中的目标函数 （12）式中，部分为运输车辆的购置费用；为在所考虑的运营周期内的货物运输费用；为配送中心的建造费用。

系统风险：有害危险物品不同于其它一般物品，在存储和运输的过程中如果处理不当便会对人类生命安全和周围环境带来严重危害。因而，有害危险物品的风险表示和风险分析/评估是有害危险物品物流管理研究的中心问题。一般而言，需要考虑的是两类风险：一是存在于配送过程中的运输风险；二是设施选址时带来的选址风险[3]。其中运输风险主要包括由于危险物资泄露对路网或周围居民造成的潜在影响，设施的选址风险主要是对环境和周围居民的影响。文献[1]提出了已有的风险表示方法主要包括：传统风险、暴露人口数量风险、危险事件概率风险、感知风险、条件风险等。本文主要采用选址风险 （主要是配送中心对周围居民造成的潜在危害）、暴露人口数量风险 （危险品道路运输过程中所覆盖的居民数量）和危险事件概率风险之和最小化作为优化目标，并将其转化为经济指标。在以下的模型中， （13）是使暴露的人口数量最小：第一部分是暴露在配送中心影响下的人口数量，第二部分为配送过程中暴露于道路沿线一定距离的居民数量；β是暴露的单位人口数量的社会成本。 （14）式是使总的危险事件发生概率之和最小，α是每一单位风险事故的期望损失。

根据以上假设和规定可以建立以下数学模型：

虽然该模型中有三个目标函数，但是由于 （13）式和 （14）式已相应的乘以一个经济转化因子β和α，使得最终的结果能够统一用货币衡量，所以该多目标优化问题实质上已转化为单目标优化问题。在实际情况中，α和β的取值一般要根据以前事故发生所造成损失的平均值或通过专家评定来给出。

3 模型应用及求解

（1） 算例描述

假设一个公司为了发展业务的需要，决定在某一城市建造若干个危险品的物流配送中心，通过调查决策者现拟定3个候选地址，各个候选点的固定建造成本和候选点周围的居民数量已知，见表1。

表1 候选点建造成本、规模及周围居民数量

另外，已知每辆运输工具的最大载重量Q为80万单位，根据市场调查结果，需求点可以分为15个，在一个配送周期内每个需求点的需求量已知，见表2。

表2 各需求点的需求量 单位：万

其它数据由excel表中随机数函数生成：各个节点的距离已知，范围6～60千米；各节点连线附近的居民数量取0.5～4.2万人；各节点连线附近的居民中心距离该路线的距离取1.0～3.0千米；各节点连线之间的道路风险取0.01%～0.08%。考虑到企业在刚开始经营时资金并不是很充足，因此管理者要求使100个配送周期内的总成本最小。

（2）模型求解及结果讨论

根据文中所建模型及初始数据，编写了求解模型的Lingo程序。运行Lingo程序，通过反复迭代运算，最终找到一个满意的可行解，在100个配送周期内的各项成本取值如表3所示，其它变量取值结果列入表4和表5中。

表3 100个周期内各项费用 单位：万元

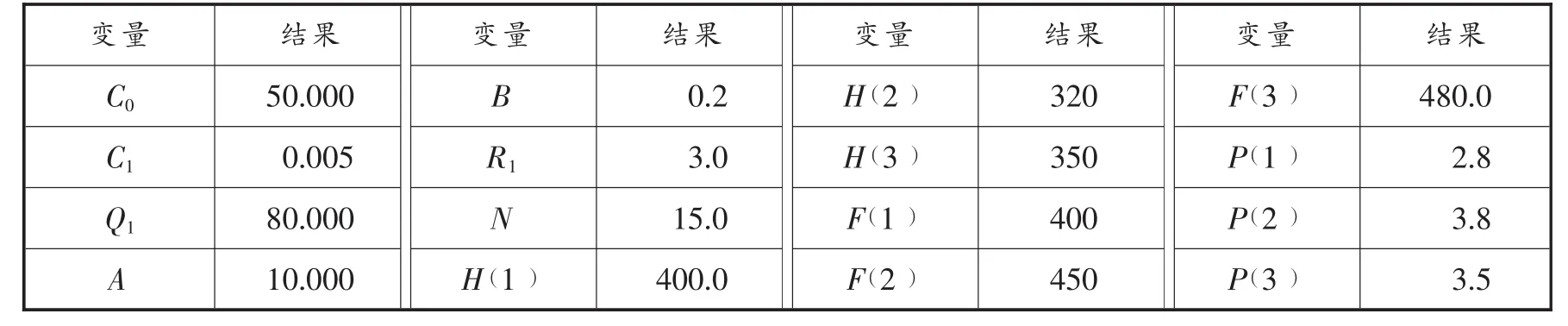
表4 模型中部分变量的取值

表5 模型中取值为1的决策变量

表4中Z（1）,Z（3 ）取值为1，表明配送中心是在候选点1和候选点3之间进行选址。决策变量Xijk取值为1是表示第K辆车从第i个节点到第j个节点，表5中X（ 1,4,8）=1,X（ 4,5,8）=1,X（ 5,1,8 ）=1，表示第8辆车从节点1到节点4，然后从节点4到节点5，最后从节点5返回节点1，由此生成运输路线：1→4→5→1。

同理可得其它路径，从而可得出该算例的最终选址和调运方案，如表6所示。

由表5、6可以看出，在3个候选配送中心中，选择建造候选点1和候选点3；一共使用了9辆配送车辆，其中配送中心1发出5个车次，配送中心3发出4个车次。通过计算可以发现，15个需求点的总需求量为607万单位，而任意两个配送中心的容量都可以满足该需求，因此，配送中心的容量不会对决策结果产生影响。另外通过比较可以发现，配送中心2的容量小于配送中心1，但其建造成本却比1高，而且配送中心2周围的居民数量也高于1，因此可以认为配送中心2很可能靠近城市的中心区域，建造成本中的土地使用费较高或者对附近居民危害的社会成本较高。在费用方面，除了选址费用外 （880万元），车辆购买费用 （450万元）最多，其次是危险事件发生造成的费用 （380万元），再其次是运输费用 （257万元），而暴露人口数量造成的费用最少 （239.3万元）。

表6 最终选址和调运方案

由此可见，在所考虑的运营周期内，选址费用和车辆的购买费用对总费用的影响最大，它们大约占到总费用的60.6%，其它的变动费用占总费用的比例不到40%，因此在短时期内，固定费用的大小对最终的选址起主导作用；在长期，路线选择造成的运输成本对选址决策有很大的影响。考虑到危险品本身的特点，在实际运输过程中，车辆应尽量选择那些道路交通事故发生率较小的路线，以免发生意外事故引起巨大的损失。同时，车辆也要尽可能选择那些距离较短的路线行驶以减少运输成本，而意外事故影响的人口所造成的费用最少，但两者差别不是很大。在实际情况中，暴露人口数量以及事故风险的经济转化因子的选取有可能会对最终的决策产生重大的影响。

4 结束语

危险品在运输过程中需要考虑的因素要比一般物品多，尤其是它们所带来的风险。因此以往仅仅以成本作为决策依据，并没有全面地反应出其真实的社会成本，尤其是它对居民和环境所造成的负的外部性。本文提出的将风险和危害转化为成本进行考虑，从经济学的角度看对整个社会更有利，即外部性内在化。同时，由于Lingo语言中使用集合概念，所以当求解规模变化时，求解程序结构并不变，只需修改数据即可，所以对从事物流规划的实际工作者有一定的参考价值。但是文中风险如何衡量以及风险到底会对企业造成多大的损失，这些并没有统一的标准，所以应客观地分析各种风险的具体影响以及它们的真实成本。由于选址和路线选择问题自身的难度，两者的集成问题求解起来更加困难。在本文中共有3个候选设施点，15个需求点，在配送时最多一辆车对一个需求点进行配送，基于此种考虑，最多不会超过15辆候选车辆，在此种情况下模型中的变量个数至少在18*18*15（4 860）个左右，而且这还没有考虑到额外引入的变量。而在现实中，18个节点的物流系统已经是比较小的系统了，如果要求解更大规模的物流系统，应该设计更为有效的算法，例如启发式算法，以求在有限时间内得到近似的最优解。

[1] 王刊良.有害危险物品后勤学的研究动态[J].系统工程理论与实践，2000(7):112-117.

[2] 王刊良，张朋柱.有害危险物品运输风险的量化模型[C]//第五届全国青年管理科学与系统科学论文集.天津：南开大学出版社，1999.

[3] 田绍军，张钦，周爱前.层次分析法在危险品配送中心选址决策中的应用[J].物流科技，2008(12):13-15.

[4] 左元斌.物流派送中心选址问题的理论、方法与实践[M].北京：中国铁道出版社，2007.

[5]汪寿阳，赵秋红，夏国平.集成物流管理系统中定位——运输路线安排问题的研究[J].管理科学学报，2000,3(2):69-75.

[6] 郭晓峰，郑棣华，叶耀华.基于最优配送路线的选址方法研究[J].物流技术，2001,109(4):28-30.

[7] 张静，刘鲁，陈安.“选址—路线”问题的建模与算法研究[J].北京航空航天大学学报 （社会科学版），2002,15(1):33-37.

[8] 章海峰，张敏，杨超.一类运输工具带双重能力约束的LRP问题[J].武汉理工大学学报 （交通科学与工程版），2006,30(2):220-223.

[9]张敏，杨超，杨珺,等.危险品集成物流管理系统选址——选线模型研究[J].管理科学学报，2008,2(1):1-3.

[10] 魏强.基于层次分析法的危险品储运模式决择和改造策略研究[D].成都：西南交通大学 （硕士学位论文），2004.

[11] 袁新生，邵大宏，郁时炼.LINGO和EXCEL在数学建模中的应用[M].北京：科学出版社，2007.

[12] 韩中庚.实用运筹学：模型、方法与计算[M].北京：清华大学出版社，2007.