基于T-不变量分解法获取工作流中的序关系

蔡 敏 汪世义 韩俊波

（巢湖学院计算机与信息工程学院，安徽 合肥 238000）

1 引言

Aalst将工作流建模理论与Petri网理论相结合，提出了工作流网模型，同时还定义了一个正确的工作流所应该满足的soundness属性[1]。如今工作流网已成为使用最为广泛的业务流程形式化模型[2]。工作流网中活动之间的序关系包含了大量的有用的信息，在许多方面有着重要应用，如过程挖掘[3]、模型一致性度量[4]、业务流程执行监控[5]等。文献[4]讨论了sound自由选择工作流系统中序关系的可获取性。然而真实业务模型往往表现出非自由选择特性，要获取这类系统中的序关系比较困难。

利用T-不变量对复杂结构的工作流网进行分解，得到一组相对简单的子结构，再对每个子结构逐个进行分析，可以达到分而治之的目的。文献[6]对sound良构工作流网进行了分解；文献[7]利用T-不变量发现好路径；文献[8]将一个工作流网分解成一组子网，再转化为PERT图，进而分析过程模型的进度和工期。本文利用T-不变量分解法将sound自由选择系统中序关系可获取性推广到一类非自由选择系统中，指出了文献[8]中有关结论存在的错误并分析了错误的原因。

2 基本概念和术语

本节给出本文涉及的一些主要概念和表示符号，详细信息可参考文献[1][3][8]。

定义 1 三元组 N＝（P，T；F） 是一个 Petri网，当且仅当P和T分别是库所和变迁的有限集合 P∪T≠Ø，P∩T=Ø，F⊆（P × T）∪（T × P），是弧的集合，即流关系。F+是流关系的传递闭包。

定义 2 Petri网 PN=（P，T；F） 是一个工作流网，当且仅当：

（1）PN 有且仅有一个起始库所 i，即·i=Ø；

（2）PN 有且仅有一个终止库所 o，即 o·=Ø；

（3）如果在 PN 上增加一个变迁 t*，使（t*）·=｛i｝，·（t*）=｛o｝所得到的扩展网是强连接的。

在工作流网中，一个变迁可能是一个活动，也可能仅仅表示AND-split或AND-join结构。库所对应变迁的前件与后件，也可能仅表示OR-split或OR-join结构。一个工作流系统由一个工作流网和它的初始标识[i]给出，记作 S=（PN，[i]）。

定义3 工作流系统S=（PN，[i]）满足soundness属性，当且仅当：

（1）S是安全的。即对任意可达标识M和库所 p，都有 M（P）≤1；

（2）从任意可达标识M出发，都可到达标识[o]；

（3）若存在可达标识，M≥[o]⇒M=[o]；

（4）无死变迁。

定义 4 PN=（P，T；F）设是一个网， C 是 PN的关联矩阵，如果非平凡的非负整数向量X满足CTX=0，则称X为PN的一个T-不变量。T-不变量X的支集记作对于一个T-不变量Jk，如果不存在其它T-不变量Jx⊂Jk，则称Jk为最小T-不变量。

定义 5 设 PN1=（P1，T1，F1）与 PN=（P，T；F）是两个网，称PN1是PN的一个T-组件，当且仅当满足条件：

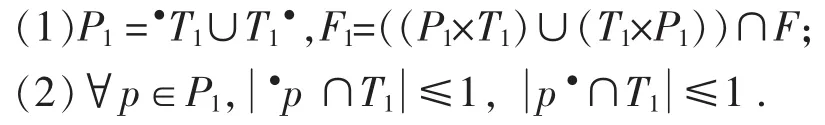
定义5第一个条件要求是PN1是PN2关于T1的外延子网，而第二个条件则要求PN1是个标识图。

3 sound自由选择系统中的序关系

定义6 Petri网是自由选择的当且仅当任意两个变迁 t1和 t2有：·t1∩·t2≠Ø 蕴含·t1=·t2.

定义7 设S=（PN，[i]）是一个工作流系统。并发关系包含所有变迁对（x，y），如果x≠y且存在可达标识M≥[x]+[y].

定义 8[4]设 S=（PN，[i]）是一个工作流系统。 弱序关系≻=T×T 包含所有变迁对（x，y），如果系统存在一个变迁发生序列σ=t1，t2…tn，使得ti=x，tk=y，1≤i＜k≤n.

在弱序关系基础上，文献[4]讨论sound自由选择系统中活动之间的几种关系：严序关系、互斥关系、交错关系以及逆严序关系。

定义9[4]设S=（PN，[i]）是一个工作流系统。变迁对（x，y）属于下列关系之一：

（4） 逆严序关系：且 y≻x.

显然，这些关系划分了T×T。文献[4]证明了在sound自由选择系统中，如果两个变迁不是并发的，那么它们的结构关系与行为关系是一致的。我们先计算出并发关系，再借助流关系的传递闭包，即可在多项式时间内计算出上述四种关系。并发关系最终可以归并到交错关系中。

4 基于最小T-不变量的结构分解技术

该分解算法存在的第一个问题是，T-不变量反映的是Petri网的结构特征，它与初始标识无关。对于sound工作流网，一个可循环执行的结构的确对应了一个T-不变量，但可能由于托肯不足的原因，一个T-不变量却不一定能对应系统的一个合法执行序列。图1给出了这样一个反例。在图1中未涂黑的变迁表示在T-不变量中权值为1。显然，该T-不变量不能对应一个合法发生序列。

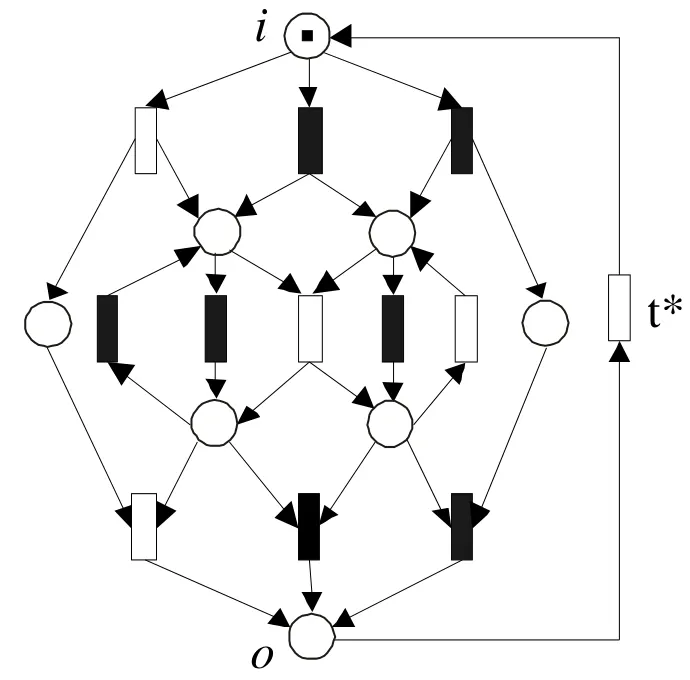
图1 一个非合法执行序列的最小T-不变量

该分解算法存在的第二个问题是，对于一个任意的sound工作流网，其最小T-不变量生成的子网未必是T-组件。例如在图2中所有变迁都在同一个最小T-不变量中，显然，这不是一个T-组件。

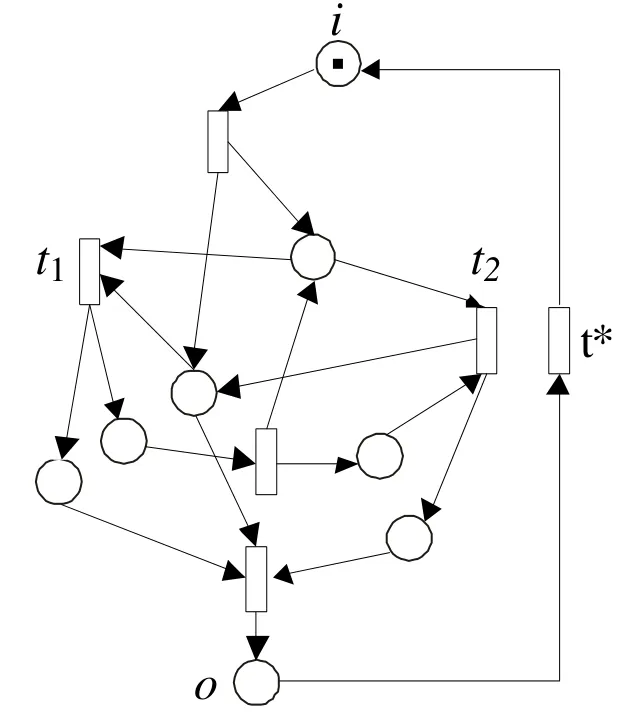
图2 一个不能生成T-组件的最小T-不变量

由于不能避免上述两个问题，文献[8]中的关于sound工作流可分解成多个T-组件子网，每一子网对应一个工作流执行分支的结论是错误的。此外，该分解算法没有考虑系统中存在可执行环情况。

然而，对于sound自由选择系统，有如下结论：

定理 1[9]设 PN＝（P，T，F，[i]）是活的且有界的自由选择系统，J是PN的一个极小T-不变量，则‖J‖生成一个强连接的T-组件，并且J是可执行的。

这一定理保证了对sound自由选择系统，可以根据最小T-不变量分解算法，得到可执行的T-组件。分解算法如下：

（2）求解方程 CTX＝0，得到所有最小 T-不变量集合，记作它们的支集集合记作注意C是的关联矩阵；

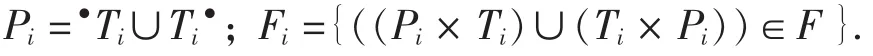
（4）所得子网分成两个集合，一个是不含t*的子网集合另一个是含t*的子网集合

（6）对合并后的每个子网，删除t*及其关联边。

考虑到T-不变量的物理意义，我们只需求解 X≥0且 X（t*）＝0或 1的 T-不变量。

5 非自由选择系统中的序关系

从第3节讨论可知，对sound自由选择系统，可根据并发关系和流关系的传递闭包来求取序关系。而对于非自由选择系统，难以根据流关系的传递闭包获取序关系。如图2，如果根据流关系的传递闭包求取序关系，t1与t2属于交错关系。但实际上t2不可能在t1之前发生，故这种交错关系不正确。

如果一个sound非自由选择系统可以通过T-不变量分解法分解成sound自由选择子系统，则其活动的序关系是可以获取的。具体步骤如下：

Step 1：基于T-不变量对系统进行分解；

Step 2：验证每个子系统是否为sound自由选择系统，若存在非sound自由选择子系统，则结束；

Step 3：依次求取每个子系统中的并发关系，并结合子系统中的流关系的传递闭包，获取严序关系、交错关系和互斥关系。

Step 4：合并第三步的结果；

Step 5：求取互斥关系。 变迁对（x，y）属于互斥关系，如果所有子系统都不同时包含x和y.

注意Step 3和Step 5都求取互斥关系，但不同的是，Step 3求取的是x=y型的互斥关系，而Step 5则求取x≠y型的互斥关系。

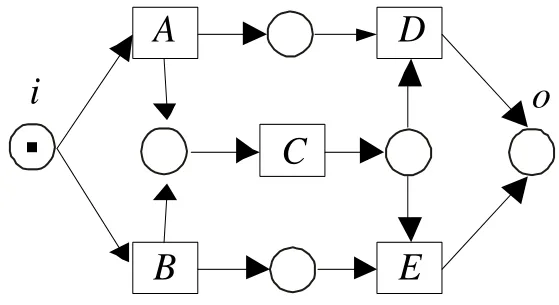
图3 一个sound非自由选择系统

图3是一个sound非自由选择系统，如果根据流关系的传递闭包，变迁对（A，E）和（B，D）将属于严序关系。然而我们可以看到，该系统只有两条可能的执行路径：A，C，D 和 B，C，E，故（A，E）和（B，D）是互斥的。如果采用T-不变量分解法，可以得到两个sound自由选择子系统，如图4所示。 在 Step 3 中可求得 （A，A）、（B，B）、（C，C）、（D，D）、（E，E）是互斥的。 在 Step 5 中，可得（A，E）、（B，D）、（A，B）、（D，E）也是互斥的。

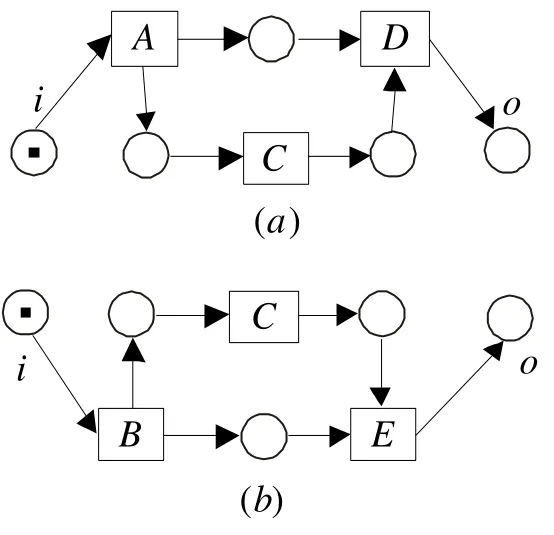
图4 图3的两个子系统

6 小结

如何获取工作流系统中活动之间的序关系，一直是模型分析人员关心的问题。本文分析了文献[8]中的错误，并给出了反例，对T-不变量分解算法做了修正。最后对sound自由选择系统获取活动之间序关系的方法进行推广，从而可以获取那些可分解为sound自由选择子系统的非自由选择系统中活动的序关系。如何获取任意sound工作流网中活动的序关系，是我们下一步要研究的问题。

[1] W.M.P.van der Aalst.The application of Petri nets to workflow management[J].The Journal of Circuits,Systems,and Computers,1998，8（1）：21-66.

[2] W.M.P.van der Aalst,K.M.van Hee,A.H.M.ter Hofstede,et al.,M.Wynn.Soundness of workflow nets：classification,decidability,and analysis[J].Formal Aspects of Computing,2011，23（3）：333-363.

[3] W.M.P.van der Aalst,T.Weijters,and L.Maruster.Workflow Mining：Discovering Process Models from Event Logs[J].IEEE Transactions on Knowledge and Data Engineering,2004，16（9）：1128-1142.

[4] M.Weidlich,J.Mendling,and M.Weske.Efficient consistency measurement based on behavioural profiles of process models[J].IEEE Transactions on Software Engineering,2011，37（3）：410-429.

[5] M.Weidlich,H.Ziekow,J.Mendling,O.Günther,M.Weske,and N.Desai.Event-Based Monitoring of Process Execution Violations[A].S.Rinderle-Ma,F.Toumani,and K.Wolf,Eds.,Proc.of the 9th International Conference on Business Process Management[C].Springer-Verlag,Berlin Heidelberg,2011：182-198.

[6] S.Pang,C.Lin,M.Zhou and Y.Li.A Workflow Decomposition Algorithm Based on Invariants[J].Chinese Journal of Electronics,2011，20（1）：1-5.

[7] H.M.W.Verbeek,W.M.P.van der Aalst,and A.H.M.terHofstede.Verifying Workflows with Cancellation Regions and OR-joins：An Approach Based on Relaxed Soundness and Invariants[J].The Computer Journal,2007，3（50）：294-314.

[8] 葛季栋，胡昊，吕建.一种基于不变量的从工作流网到PERT图的转换方法[J].电子学报，2008，36（5）：893-898.

[9] E.Best and J.Desel.Partial order behaviour and structure of Petri nets[J].Formal Aspects of Computing，1990，2（1）：123-138.