利用Excel进行流网的简单绘制

摘 要：渗流场的流网图一般由实验得出，利用excel的迭代功能可以简化流网的绘制过程，将Excel迭代产生的数据导入matlab可以得出质量较好的流网图。

关键词：流网;Excel;matlab;迭代

1.原理介绍

稳定的渗流场中，一组流线和等势线组成的网格称为流网图，利用流网可以确定渗流的诸多要素。对二维渗流场的拉普拉斯方程进行五点差分，可以得出渗流场流函数及势函数的迭代公式，作为常见数学分析工具的Excel，具有很强的数值处理能力。本文利用Excel的迭代功能求解二位渗流的拉普拉斯方程，可以得出渗流场的流网图。

2.势函数值求解

我们可以假设上游水位15m，下游水位5m，并给定渗流区域的初始边界为：长250m，宽100m，边界轮廓线看作流线，每天与其相交的势函数线要与其垂直。将此区域离散化为251×101个方格。

2.1设定边界条件

由于边界很大，需要的单元格数目很多，计算时我们选择了Excel2010版本。

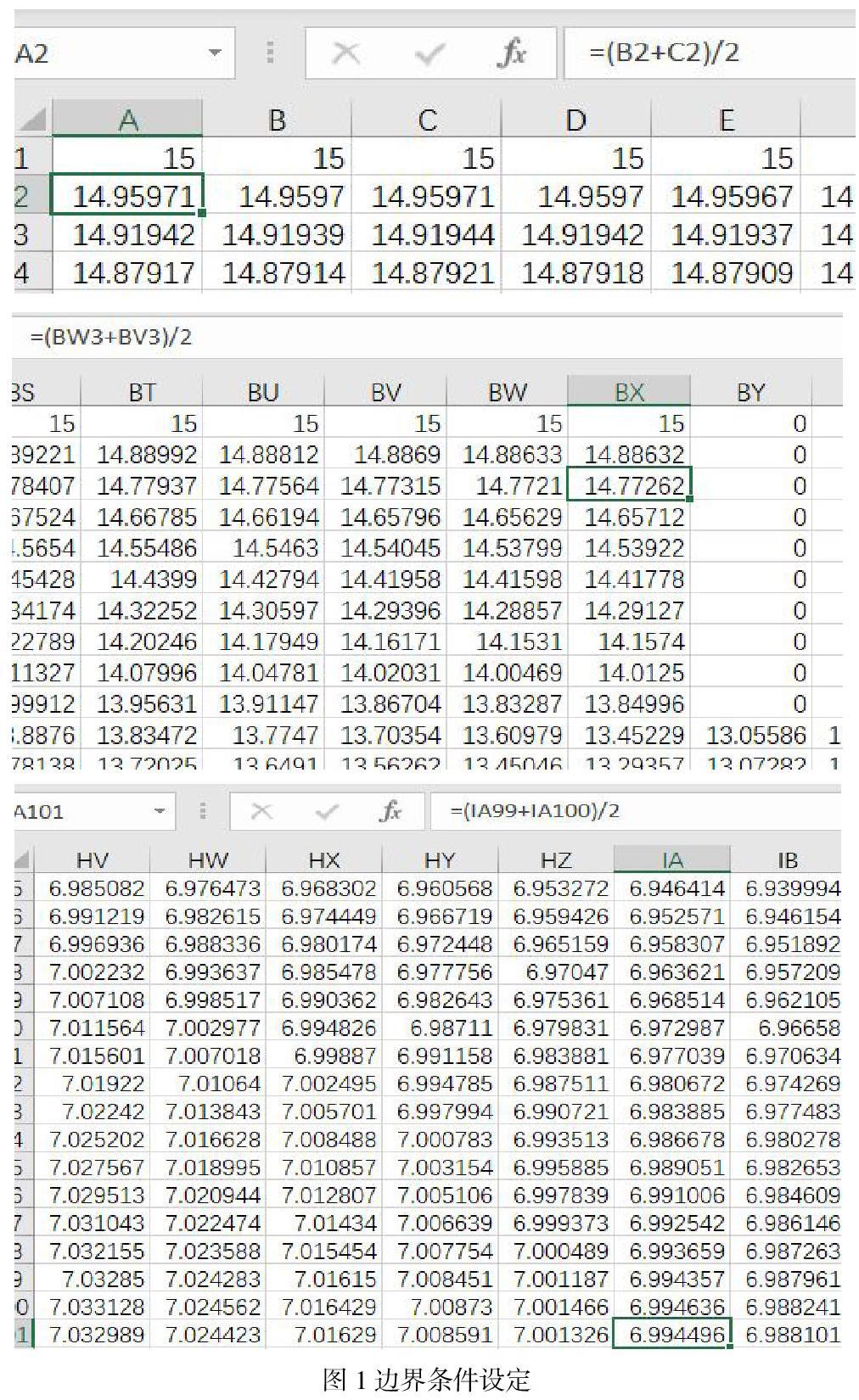
离散后的每个方格为Excel的一个单元格，共有251列、101行，闸基上游边界区域我们将其赋值为15，闸基下游边界我们将其赋值为5。渗流区域的外边界我们将其赋值为其内侧两行或两列的均值，其中，闸基所在位置无水流通过，将其赋值为0。如图1所示。

2.2迭代功能的实现

内部网格的所有求解表达式均为周围网格值的均值，比如B3=（B2+B4+A3+C3）/4。在Excel窗口中点击“文件”    “选项”    “公式”，设定迭代次数和迭代精度，为保证生成渗流网足够光滑，我们设置迭代30000次，精度0.00001。

3流函数值求解

流函数的求解相对简单，可将除上游边界以外的外边界网格值设置为15，第一行的网格值设置为齐下两行的网格值的平均值，如B2=（B3+B4）/2。其余单元格的值设置为周围单元格的值的均值。闸基所在位置的流函数值同样设置为0。

4利用matlab绘制流网图

将势函数及流函数迭代产生的值导入matlab中，编写一个简单的程序，命令如下：

clear all

l=xlsread（'Laplace.xlsx'，1，'A1：IQ101'）;%读取表一

s=xlsread（'Laplace.xlsx'，2，'A1：IQ101'）;%读取表二

[x，y]=meshgrid（1：251，1：101）;%x，y为101行，251列的矩阵

%

figure%呼出图片

[C1，h1]=contour（x-1，-y+1，s，quantile（s（：），25），'r'，'showtext'，'off'）;%由于表格从坐标（1，1）开始读取，故取x-1，y-1，且需要纵坐标取负数

h1.LineColor='r';

hold on

[C2，h2]=contour（x-1，-y+1，t，'LevelList'，[2.1 4.1 6.1 8.1 9.5 10.5 11.5 12.5 13.5 14.5]）;%绘制两种渗流线

h2.LineColor='b';

x=[0 75 75 80 85 165 170 175 175 250 250 0 0];

y=[0 0 -10 -10 -5 -5 -10 -10 0 0 -100 -100 0];

plot（x，y，'r-'）;%描出边界

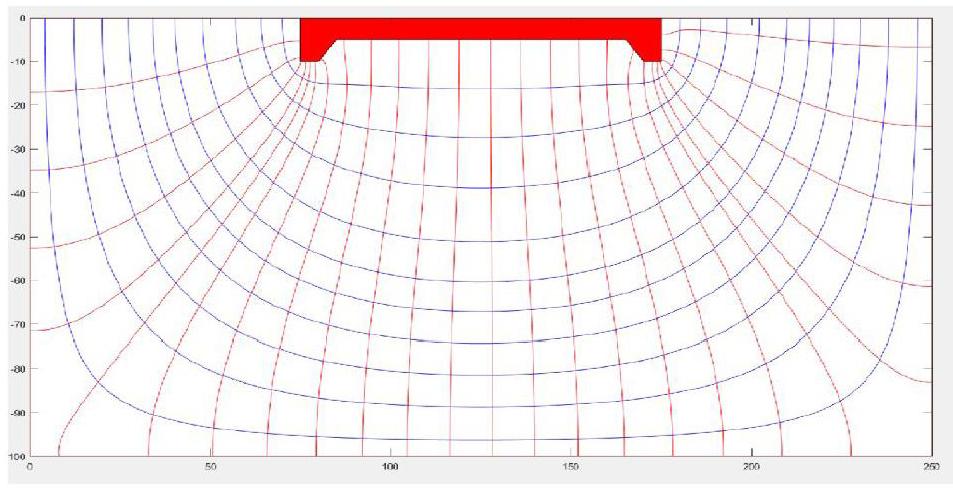
運行程序后，得到了一张流网图，如下图所示。

该流网图与实际效果拟合的很好。

5.总结

本文是作者毕业设计中渗流场网格划分的一部分，避免了繁杂的水电比拟法，希望能够对同类设计提供借鉴。

参考文献：

[1]赵智涛.复杂边界条件下流网的简易绘制方法.

[2]贾新民、严文.有限差分法求解拉普拉斯方程.

作者简介：

陈丙舒（1998.09-）男，汉族，黑龙江省齐齐哈尔市，本科生，研究方向：水利水电工程