多自由度伺服机构负载模拟系统动态特性研究

孙萌，李长春，延皓，刘晓东，张金英，母东杰

(北京交通大学机械电子控制工程学院，北京100044)

0 引言

负载模拟器是运载火箭和飞行器舵机系统设计过程中重要地面试验设备之一，用以模拟飞行器在飞行过程中舵面所受空气动力力(矩)载荷谱［1］，检测伺服机构产品的技术性能;另一方面，在伺服机构的改进研究及新机构的开发中，负载模拟系统可模拟不同规格的负载实物，提供各种状态下的测试数据，从而节省大量研发费用并缩短研制周期［2］。目前，国内外大型负载模拟系统按照驱动方式一般分为机械加载、液压加载及电动加载。相对电动加载而言，液压加载出力大，频宽高，加载具有较高灵活性［3］，其缺点是多余力以及响应滞后等。机械加载的优点在于精度高，缺点是结构复杂及灵活性不足。

对于大推力运载火箭而言，原有的推力矢量伺服系统(TVC)负载模拟设备已经不能满足要求。由于负载模拟器使用领域的特殊性和敏感性，国外这方面的研究文献并未多见，且主要集中在控制算法的研究上。近年来，随着国内国防工业的发展，关于负载模拟器方面的研究越来越多，但多数集中于消除加载多余力矩的控制算法的优化与研究上，对模拟执行机构的多自由度特性方面涉及较少。文献［4］只是从位置同步控制研究的角度提出了一种提高系统频宽的方法，并未涉及伺服机构的多刚度特性;文献［5］讨论了运载火箭伺服机构负载特性与无发动机空载特性和有发动机空载特性间的转换关系，但没有考虑伺服机构的安装刚度与发动机负载的多刚度特性;文献［6］分析了舵机负载模拟器的多刚度特性，但是没有进一步研究执行机构的各主要参数与系统频率特性的对应关系;文献［7］虽然从仿真角度分析了推力矢量伺服机构多自由度特性与结构参数之间的关系，但缺乏实验数据支持。现有的推力矢量伺服机构负载模拟器，无法模拟多刚度伺服系统实际工作状态下负载运动的双谐振峰现象。

针对运载火箭伺服机构的谐振特性，本文提出一种包括机械和液压加载的新型综合式负载模拟系统，能够模拟伺服机构的双谐振峰现象，并通过改变相应的机械参数调整双谐振峰位置。对于此多自由度伺服控制系统，文中对其动态特性进行建模和仿真，并通过原理性实验表明其模拟伺服机构动态特性的可行性，从而为负载模拟系统的设计提供理论依据和数据支持。

1 推力矢量伺服机构特性分析

1.1 问题提出

运载火箭的推力矢量伺服机构负责推动发动机及喷管摇摆运动，其工作原理见图1.一般情况下，在相互垂直方向上有相应的两个伺服机构，通过控制两伺服机构各自的伸长量，来控制发动机喷管在垂直两方向上摆动，以实现喷管在空间中的任意角度。伺服机构由电液伺服阀、液压作动筒以及液压源组成。伺服阀作为伺服机构的控制元件，控制液压作动筒的伸缩。液压源可以独立设置也可以与伺服机构做成一体。图1中画出了其中一个伺服机构的情况。

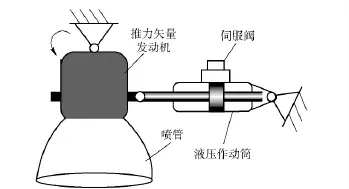
图1 推力矢量伺服机构工作原理Fig.1 Schematic diagram of thrust vector servo control mechanism

整个推力矢量伺服机构系统结构复杂。一方面，整个喷管体现出一种复杂的柔性特点［8］;另一方面，限于实际工作环境，伺服机构支撑部分也存在一定的柔度。对推力矢量伺服机构进行建模时，若考虑作动筒的质量、伺服机构支撑刚度以及发动机的柔度，则伺服机构为一多自由度电液伺服系统［9］。在伺服机构带矢量发动机负载频率特性实验中，液压作动器指令输入与矢量发动机喷管角位移输出在动态响应上表现出双谐振峰的特性，其频率特性见图2.此频率特性反映了伺服机构与负载发动机的综合动态特性。

由此可见，新型号矢量发动机的动态确实呈现复杂的多自由度特性。而负载模拟的目标，是为真实的推力矢量伺服机构模拟一个负载环境，在此架构下用各种频率的信号驱动伺服机构，其负载输出的响应特性必须与目标负载(即矢量发动机负载)频率特性(见图2)一致。这也成为多自由度推力矢量伺服机构负载模拟系统最重要的设计依据。

图2 目标负载频率特性Fig.2 Target frequency characteristic of load

为了能够设计满足要求的负载模拟系统，需要对推力矢量伺服机构进行模型建立与仿真，并分析系统的动态特性，确定矢量喷管的频率响应中的谐振峰与哪些因素有关。

1.2 机构模型分析

对于推力矢量伺服机构来说，所受负载包括:惯性负载、弹性负载、摩擦负载以及常值负载等，那么一个完整负载模拟系统应包括对以上负载的模拟。

要对推力矢量伺服机构建立数学模型，应当考虑伺服机构的支撑刚度，作动筒的质量，负载质量，发动机喷管自身的柔度特性折算到活塞杆处的等效刚度，发动机质量及喷管端质量。由于液压加载存在相位的滞后和幅值的衰减，而相位滞后有可能使得模拟出的惯性及弹性负载特性与实际相差较大，因此本系统中惯性负载和弹性负载由机械结构模拟。图3为负载模拟系统原理图，常值负载对系统的影响不大因而图中未体现。其中:K1为等效支撑刚度，K2为质量块连接刚度，KL为弹性负载等效刚度，B1为弹性支撑等效阻尼系数，B2为质量块连接等效阻尼系数，Bc为活塞与作动筒摩擦阻尼系数，BL为摩擦负载等效阻尼系数，mT为作动筒等效质量，mp为大质量块质量，ms为小质量块质量。

图3 负载模拟系统原理图Fig.3 Schematic diagram of load simulation system

从图3中可看到，在负载模拟系统中，为了降低结构的复杂性，用平动的惯性负载等效代替发动机和喷管的转动惯量负载。为了模拟发动机负载的自身柔度，将发动机负载等效为一大质量块与一小质量块由一弹簧阻尼器并联组成。负载模拟系统的伺服机构安装在一个非刚性的结构上，而负载本身也存在一定的柔性结构(用弹簧连接大、小质量块模拟)，因此此系统与伺服机构实际工作环境和负载的特点是近似的。显然，这是一个多自由度液压伺服系统，在此基础上可以通过改变各环节的刚度、质量，深入分析系统的频率响应特性。

2 多自由度伺服机构建模及仿真

2.1 伺服机构模型建立

为了分析图3所示机械结构的动态响应特性，并验证系统各参数与频率特性的关系，以设计出达到要求的负载模拟系统，对此伺服机构进行数学模型的建立。

虽然阀控液压系统本身是一个非线性系统，但对于推力矢量伺服系统来说，阀芯总是在中位反复运动，且位移很小，故可将伺服阀系统模型线性化。阀芯位移与负载流量关系式如下:

式中:xv为阀芯位移;QL为负载流量;PL为负载压力。

如图3所示:yT为作动筒位移，yp为大质量块位移，ys为小质量块位移，以伺服阀芯位移xv为系统输入，小质量块位移ys为系统输出，对伺服机构位置系统进行建模。

定义状态变量:

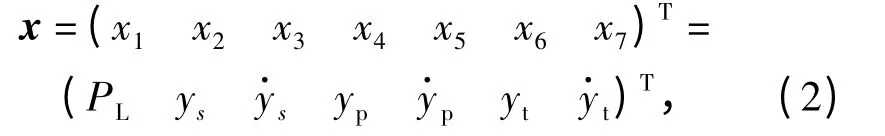
式中x3、x5、x7分别为小质量块、大质量块以及作动筒的运动速度。

定义输入输出变量:

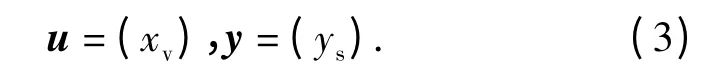
则伺服机构系统可表示为如下的状态方程形式:

式中:βe为液压体积弹性模量;Vt为作动筒有效容积;Kq为伺服阀流量系数;A 为活塞杆有效工作面积;Kce为总流量-压力系数。

需要指出的是，(4)式是以阀芯位移作为控制输入的。若以伺服阀输入电流I 为控制输入，Gsv(s)代表伺服阀的动态特性，可以得到如图4的伺服机构数学模型框图。Gsv(s)通常按照二阶环节考虑。

以上就得到了考虑系统支撑柔性及负载柔性的完整的伺服机构状态方程模型及其框图。

其中活塞相对于液压作动筒的位移记作yd，则

图4 伺服机构状态方程模型框图Fig.4 Model diagram of servo mechanism state equations

以活塞相对位移yd为输入，大小质量块位移yp和ys分别为输出的位置伺服系统的频率特性是本文所要研究的。由上述状态方程(4)式可得yd到ys的传递函数

式中G(s)的表达式为

对于负载系统，伺服机构的传递函数可以简化为两个二阶环节串联如下:

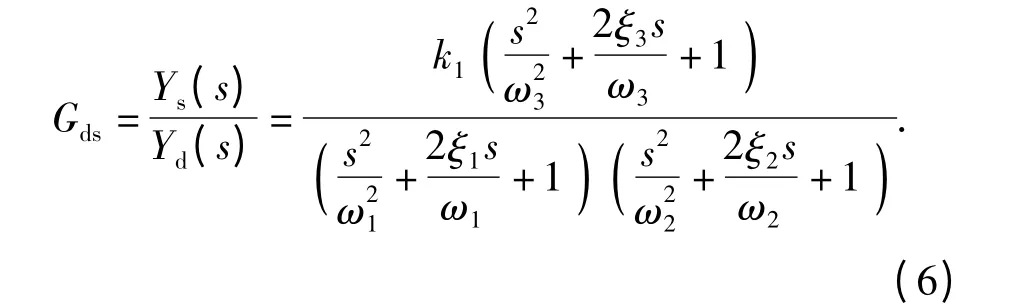
yd到yp的传递函数Gdp为

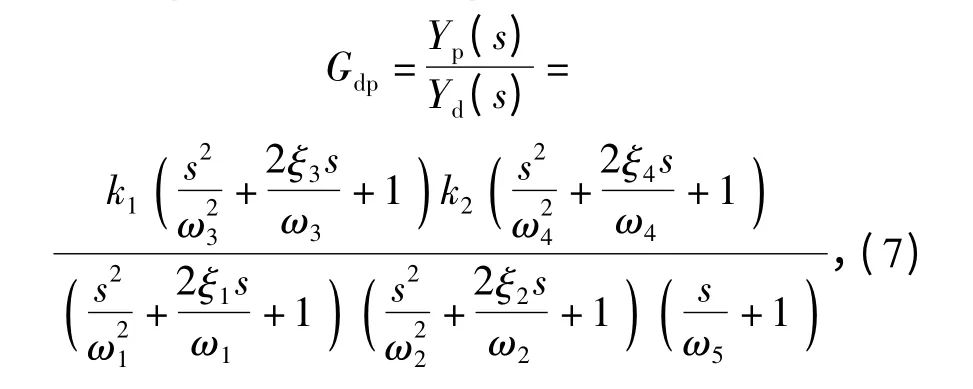
2.2 伺服机构系统仿真分析

控制系统除了包括伺服阀控液压缸所组成的伺服机构外，还包括数字控制器、伺服阀驱动电路，加入位移传感器反馈信号后构成位置闭环系统。根据伺服机构控制系统的实际情况，具体参数见表1.

表1 系统主要参数表Tab.1 List of system chief parameters

系统安装刚度K1在5×106～12×106N/m 之间调节，大小质量块连接刚度K2在0.5 ×106～1 ×106N/m之间调节，大质量块mp在800～1 400 kg之间调节，小质量块ms在30～80 kg 之间调节。分别取典型值K1=5×106N/m、K2=1×106N/m，mp=1 400 kg，ms=80 kg.使用Matlab 仿真建模软件对系统进行仿真，得到如图5所示yd到yp及yd到ys传递函数bode 图。

如图5(a)为yd到yp传递函数幅频特性，图5(b)为yd到ys传递函数幅频特性。由图5(b)可明显看出，系统在频率为57.5 rad/s 及116 rad/s 处分别出现了一阶和二阶两个谐振峰，即(6)式中ω1=57.5 rad/s，ω2=116 rad/s.由于系统存在支撑柔度特性的缘故，在更高频的区域出现了一个反谐振峰，通过(6)式分析，固有频率ω3=267 rad/s.由于处于高频段，根据实际系统的工作特性以及设计要求，对此反谐振峰并不进行研究，只对一阶和二阶谐振峰进行深入分析。

观察(6)式与(7)式，发现由于传递函数Gdp比Gds多了一个二阶微分环节和一个惯性环节，故在幅频特性上有所表现。除仍含有ω1与ω2处的双谐振峰及ω3处的反谐振峰外，在ω4=112 rad/s 处出现了一个新的反谐振峰。由于此反谐振峰的存在，对系统二阶谐振频率产生了明显的对消作用，使得ω2所对应的二阶谐振峰值大大降低。ω4与ω2越接近，对消作用越明显。由于惯性环节转折频率ω5≫ω2，故不进行研究。

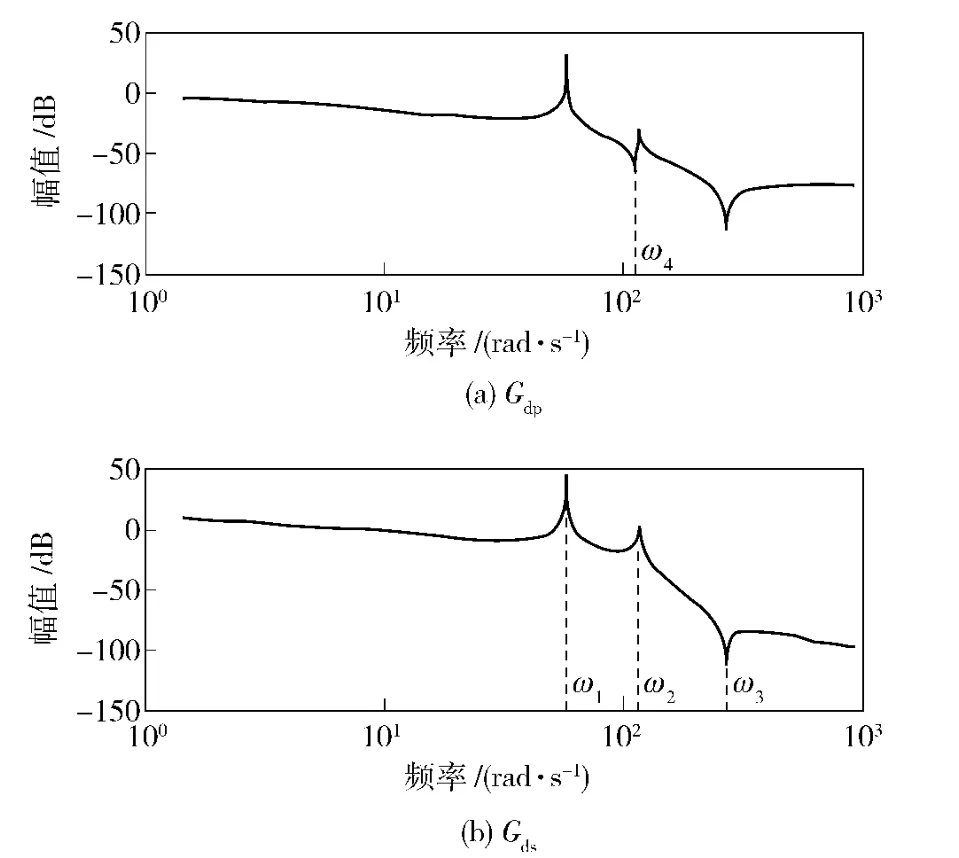
图5 闭环系统bode 图Fig.5 Bode diagram of closed-loop system

由于负载模拟系统是通过调节合适的系统支撑刚度K1、大小质量块连接刚度K2以及大小质量块质量mp、ms来使系统的幅频特性达到期望的效果，因此本文将主要研究上述4 个参数的变化对系统幅频特性有哪些影响。由于阻尼系数的变化只影响到谐振峰的幅值，且影响较小，故不进行深入分析。

首先保证其他参数如前所述不变，分别单独改变K1、K2、mp、ms四个参数，得到如图6～图9所示闭环系统bode 图。

由图6～图9可以看出，无论传递函数Gds亦或是Gdp，一阶谐振频率ω1主要受系统支撑刚度K1与大质量块mp的影响，二阶谐振频率ω2主要受大小质量块连接刚度K2与小质量块ms的影响。也就是说，一阶谐振频率体现了系统的支撑柔度特性，而二阶谐振频率则体现了系统的负载柔度特性。而对于传递函数Gdp，由2.1 节推导，二阶微分环节的谐振频率ω4与二阶谐振频率ω2同样主要受K2与ms的影响。

将参数的变化与谐振峰固有频率一一对应不难发现，ω1随支撑刚度K1的增大而增大，随大质量块mp的增大而减小。ω2与ω4均随连接刚度K2的增大而增大，随小质量块ms的增大而减小，且ω2＞ω4.当ms增大时，ω4减小的幅度要大于ω2，ω4逐渐远离ω2;当ms减小时，ω4增大的幅度亦大于ω2，ω4逐渐接近ω2，反谐振峰的对消作用愈加明显。当ms减小为0 时，也就是说负载只有大质量块mp时，两传递函数合二为一，且二阶谐振峰消失。系统表现为一个二阶振荡环节。这与实际情况相符，这也说明了理论分析的正确性。

图6 K1变化时闭环系统bode 图Fig.6 Bode diagram of closed-loop system in changing K1

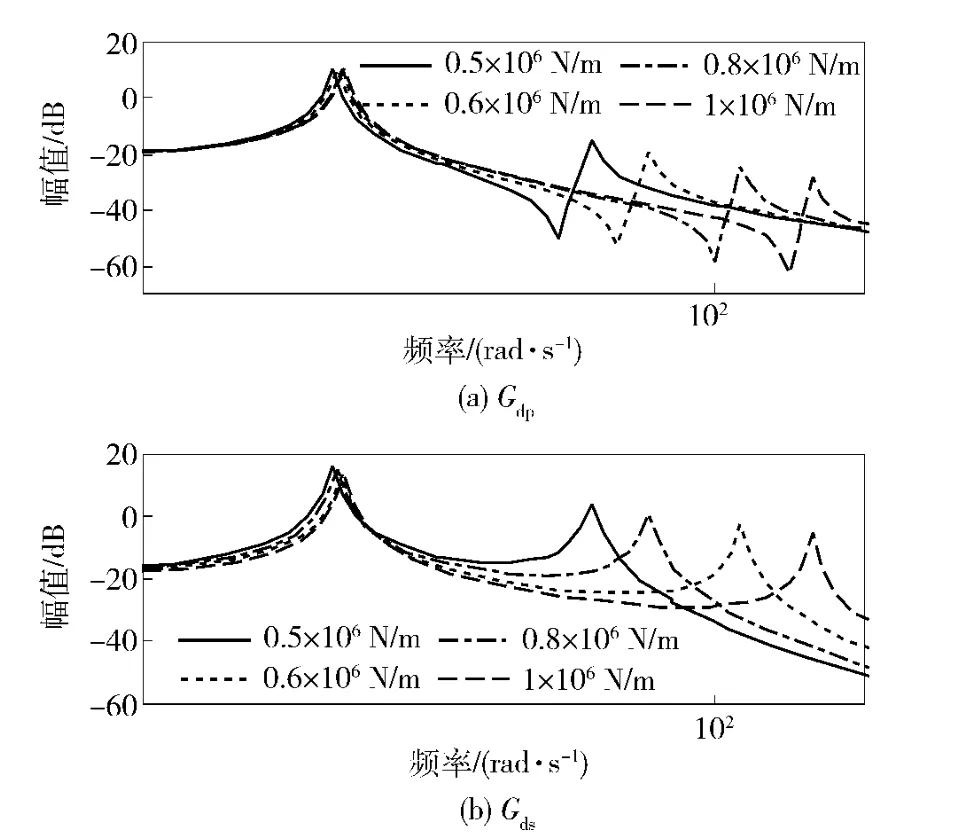
图7 K2变化时闭环系统bode 图Fig.7 Bode diagram of closed-loop system in changing K2

有上述分析，可以单独调节K1或mp的数值来配置一阶谐振峰的位置，即改变一阶谐振频率的大小;同样的，也可以单独调节K2或ms的数值来改变二阶谐振频率的大小。一阶及二阶谐振峰的阻尼比大小，主要由粘性阻尼系数B1、B2、BL等参数决定。这样就能构造出与实际系统相同的频率特性，从而使负载模拟系统能够准确地复现实际系统的动态响应特性，并通过进一步的实验对推力矢量伺服机构进行深入的性能研究，为性能的改善提供数据支持。

图8 mp变化时闭环系统bode 图Fig.8 Bode diagram of closed-loop system in changing mp

图9 ms 变化时闭环系统bode 图Fig.9 Bode diagram of closed-loop system in changing ms

3 实验研究

为了验证多自由度负载模拟系统的可行性，建立了如图10 所示的原型实验系统，如图所示，T 型旋转架mp用于模拟推力矢量发动机，由于发动机相对于喷嘴结构较为集中，因而等效为一个大质量块。相对于发动机，喷嘴的刚度较小，且质量相比较轻，因而等效为一个附加的质量弹簧系统，K2为等效连接刚度，小质量块ms则用来等效喷嘴质量。安装刚度特性则由刚度支撑板K1进行模拟。K1、K2的大小均可通过改变固定点间的长度进行连续改变。大小质量块也可以直接更换，从而改变mp、ms的参数值。这样可以通过对不同负载质量、连接刚度及安装刚度的伺服机构系统进行动态特性测试。通过连续改变上述机械参数，就可以确定矢量发动机动态的谐振峰分别与哪些因素有关，并得到与设计要求一致的机械参数设计结果。

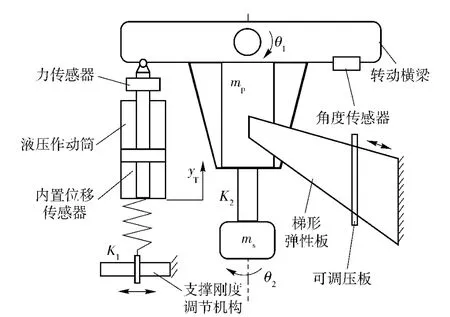
图10 多自由度伺服机构动态特性模拟装置原理图Fig.10 Schematic diagram of multiple-DOF servo mechanism dynamic characteristics simulator

具体参数如下:大质量块150 kg;小质量块39 kg;弹性连杆为45#钢;液压缸活塞直径80 mm，活塞杆直径45 mm，行程500 mm;伺服阀为偏导射流型，空载流量100 L/min，驱动电流-10～10 mA;实验压力10 MPa，最高压力20 MPa.扫频实验结果见图11.

图11 K1变化时实际闭环系统幅频特性Fig.11 Magnitude-frequency characteristic of real closed-loop system in changing K1

通过扫频实验得到的实际系统的幅频特性可以明显看出，系统在中低频段具有双谐振峰特性。由系统bode 图可以看出，传递函数Gds以及Gdp在刚度条件一致的情况下，ω1及ω2均相同。刚度K1为5 ×106N/m 的情况下ω1均为43.98 rad/s，ω2均 为69.12 rad/s.当刚度K1增大到7.5 ×106N/m 时，ω2为69.74 rad/s，基本保持不变，而ω1则增大到了52.78 rad/s，这与仿真结果一致。从Gds与Gdp的幅频特性曲线比较可以看出，后者的幅频曲线在接近二阶谐振频率ω2处确实存在一个反谐振峰，所对应的谐振频率ω4在刚度K1不同的情况下分别为65.97 rad/s 和66.6 rad/s，基本不变，同样验证了仿真结果的正确性，说明负载模拟系统采用上述机械结构设计来模拟推力矢量伺服机构的频率特性是切实可行的。

由于仿真模型为一个理想物理系统，而实际系统通过各种环节进行连接，存在多个连接刚度，实际等效刚度为多个刚度耦合串联，肯定比计算刚度要低，因此实际系统的一阶与二阶谐振频率均比仿真结果要小。但仿真模型与原型实验系统的分析结果都与实际系统的负载频率特性相一致，表明此多自由度结构能够准确模拟推力矢量发动机的动态特性。实际负载模拟系统一阶谐振频率要求为65 rad/s，二阶谐振频率则要求在80～100 rad/s 之间任意调节。

4 结论

1)针对推力矢量伺服控制系统的地面实验，本文提出一种多自由度负载模拟系统，能够对伺服机构的惯性负载、弹性负载和摩擦负载等进行有效模拟。

2)建立负载模拟系统的数学模型，仿真表明此系统中负载的位置输出呈现出双谐振峰特性，与推力矢量伺服机构全物理实验结果一致，表明用此负载模拟系统复现伺服机构频率特性是可行的。

3)仿真分析中，通过反复改变主要参数进行仿真，发现了双谐振峰谐振频率随参数变化的规律，为构造真实系统的频率特性提供了手段。

4)建立了负载模拟原型实验系统，负载的扫频实验中成功体现了双谐振峰的特点，并通过调节系统参数验证了双谐振峰谐振频率变化规律，从而为负载模拟系统的研制奠定基础。

References)

［1］ Liu Xiao-dong，Li Chang-chun，Zhang Jin-ying.Study on auto tracking electro-hydraulic servo system for rail crack detection vehicle［C］∥6th International Conference on Fluid Power Transmission and Control.Hangzhou:Zhejiang University，2005:247 -251.

［2］ 华清.电液负载模拟器关键技术的研究［D］.北京:北京航空航天大学，2001.HUA Qing.Studies on the key technology of electro-hydraulic load simulator［D］.Beijing:Beihang University，2001.(in Chinese)

［3］ Shang Yao-xing.Study on friction torque loading with an electrohydraulic load simulator［J］.Chinese Journal of Aeronautics，2009，22(6):691 -699.

［4］ 张立勋，孟庆鑫，刘庆和，等.位置同步补偿克服负载模拟器干扰力矩及提高系统频宽的理论与实验研究［J］.宇航学报，1997，18(1):120 -123.ZHANG Li-xun，MENG Qing-xin，LIU Qing-he，et al.Experimental and theoretic study on eliminating the disturbance torque and widening the frequency band width of the load simulator using position synchro compensation［J］.Journal of Astronautics，1997，18(1):120 -123.(in Chinese)

［5］ 张洁，孙凝生.运载火箭伺服机构负载与空载特性间的转换传递函数［J］.航天控制，2000，18(2):12 -16.ZHANG Jie，SUN Ning-sheng.The transfer function between servo sector load of launch vehicle load and no-load characteristics［J］.Aerospace Control，2000，18(2):12 -16.(in Chinese)

［6］ 尚耀星，吴帅，焦宗夏，等.基于极限性能要求的电液负载模拟器多刚度与非线性复合数学模型［J］.航空学报，2009，30(7):1332 -1340.SHANG Yao-xing，WU Shuai，JIAO Zong-xia，et al.Electro-hydraulic load simulator based on ultimate performance requirements and the mathematical models with nonlinear［J］.Journal of Aeronautics，2009，30(7):1332 -1340.(in Chinese)

［7］ 朱晓敏，延皓，孙萌.多自由度伺服机构负载模拟系统建模与实验研究［J］.兵工学报，2011，32(5):602 -606.ZHU Xiao-min，YAN Hao，SUN Meng.Modeling and experimental investigation of multiple DOF servo mechanism’s load simulator［J］.Acta Armamentarii，2011，32(5):602 -606.(in Chinese)

［8］ 李洪人.液压控制系统［M］.北京:国防工业出版社.1990.LI Hong-ren.Hydraulic control system［M］.Beijing:National Defense Industry Press，1990.(in Chinese)

［9］ 谈宏华，张业建.多自由度电液伺服系统动态特性研究［J］.液压气动与密封，2006，(3):39 -41.TAN Hong-hua，ZHANG Ye-jian.Study on dynamic performance of multi-DOF electro-hydraulic servo system［J］.Hydraulics Pneumatics ＆ Seals.2006，(3):39 -41.(in Chinese)