横向增强芯材的等效弹性模量研究

李 飘，陈美霞，罗 琦

华中科技大学船舶与海洋工程学院，湖北武汉430074

0 引 言

近年来，复合材料科学与工业技术发展迅速，其应用范围日趋广泛，在航空、航天、汽车、舰船和建筑等领域发挥的作用越来越显著，这与复合材料具有比强度和比模量高、减振降噪性能优良、耐腐蚀性强、耐热性好以及具有可设计性等突出的优点关系密切。特别是在舰船等军事装备的应用方面，由于其所处环境恶劣以及作战攻防需求，既要求结构具有较强的抗爆、抗冲击、抗疲劳性，还必须保证其具有优良的隐身性。

在目前舰船结构设计日趋成熟的情况下，复合材料是改善舰船强度和隐身性等指标的重要且有效的突破点之一。在多种复合材料结构中，泡沫夹芯板的应用历史悠久，应用范围广泛。与普通单一材料相比，泡沫夹芯结构不仅具有比强度高、比刚度大等特点，还具有隔音、防热和减振等功能特性。但是，泡沫夹芯结构的层间性能和面外抗压性能相对较弱。为了改善泡沫芯子的力学性能，提高夹芯结构的整体力学性能，可以采取在泡沫芯层中增加横向增强构件等措施，如圆柱体支柱和长方体支柱等。

对于这种横向增强夹芯层合板结构，分析其力学性能的第一步就是要求解出含有横向增强构件的芯层等效弹性模量。Zhao 等［1］在Eshelby-Mori-Tanaka 理论的基础上提出了两相复合材料等效模量张量，并将其与Hill 与Hashin 的上下限进行了比较。刘文辉等［2］用ANSYS 有限元程序对单胞进行求解，得到了复合材料的等效弹性模量，分析了不同微观结构对材料等效弹性模量的影响，并与实验和其他理论结果进行比较，最后得到了不同方向的方形纤维对于材料的有效模量和有效泊松比的影响。王兵等［3］采用等效夹杂理论，并引入基于实验数据的修正系数，结合Mori-Tanaka 方法预报了纤维柱增强泡沫芯材的法向弹性模量和横向剪切模量，具有很好的准确性，并进一步探讨了纤维柱内纤维体积含量及纤维柱直径的变化对芯子等效性能的影响。

雷友锋等［4］采用细观力学有限元法，通过对复合材料细观结构代表性体积单元的力学响应计算，得到了宏观等效弹性模量。在该计算方法中，给出了施加简便的边界载荷以及恰当的边界变形约束条件的方法。数值计算结果与部分试验结果具有较好的一致性，表明所提出的方法能较好地计算复合材料的宏观有效弹性模量。刘振国等［5］对三维四向编织复合材料的参数化建模技术进行了研究，采用有限元软件较真实地模拟了该材料的细观结构。在此基础上，讨论了相应的边界条件和约束条件的施加，并应用有限元方法计算了该材料的纵向和横向弹性模量。通过与实验结果的对比，表明计算结果的预报精度较好。

本文将采用基于Eshelby 等效夹杂原理的Mo⁃ri-Tanaka 方法，求解出含横向增强构件芯材的等效弹性模量，包括拉伸模量、剪切模量和泊松比。同时，采用有限元软件ANSYS 对芯材元胞进行数值模拟，计算出等效弹性模量，并与Mori-Tanaka方法的计算结果进行对比。在对理论求解进行验证的前提下，将继续研究基体和增强构件的材料属性和尺寸参数等因素对芯层等效弹性模量的影响规律。

1 理论基础

1.1 等效夹杂理论

Eshelby［6-7］关于无限大体内含有椭球形夹杂弹性场问题的一个重要研究结论是：当本征应变均匀（对本征应变颗粒）或外载均匀时（对非均匀颗粒），椭球颗粒内部的弹性场也是均匀的，可用椭圆积分的形式表示。这个解后来成为等效弹性模量计算的基础，即在各向同性无限大弹性体中，发生了均匀的本征应变，当其为常数时，椭球体Ω 内的应变εij是均匀的，它可表示为

式中，Sijkl为Eshelby 张量，它与基体的弹性性质及夹杂的形状有关，其表达式可参考文献［8］。

1.2 Mori-Tanaka 方法

Mori 和Tanaka［9］在研究弥散硬化材料的加工硬化时，提出了求解材料内部平均应力的背应力方法，即Mori-Tanaka 方法。

设均质材料在其边界上受到远场均匀的应力σ0的作用，其本构关系为

式中，L0为基体材料的弹性常数张量。其他条件不变，当基体中存在夹杂相时，夹杂之间的相互作用会产生一个扰动应变。复合材料基体中的平均应力为

显然，基体中应力的扰动部分为

由于材料弹性性质存在差别，在外力作用下，复合材料夹杂相内的平均应力和平均应变不等于基体内的相应平均值，他们的差值分别为σ′ 与ε′。这个在基体平均背应力σ0+σ～ 基础上夹杂的应力扰动问题可以用Eshelby 等效夹杂原理处理，即

式中：L1为夹杂相的弹性常数张量；ε*为夹杂的等效本征应变；σ′与ε′为由于单个夹杂的存在而相对于原本的基体所引起的扰动应力和应变，采用Eshelby 的推导结果有

式中，S 为Eshelby 四阶张量。

根据文献［8］的推导，复合材料的体积平均应力σˉ应等于其远场作用的均匀应力σ0，且有以下关系式：

式中，C1为夹杂相的体积比例。结合式（3）和式（5），可以得到

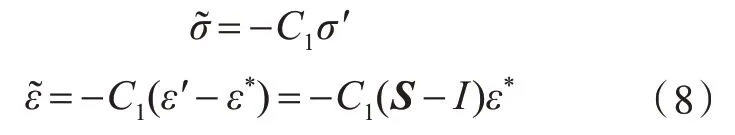
将式（6）和式（8）代入式（5），得到：

式中，

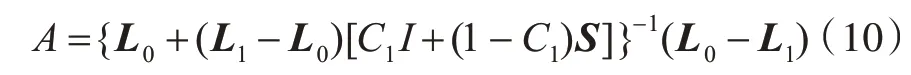
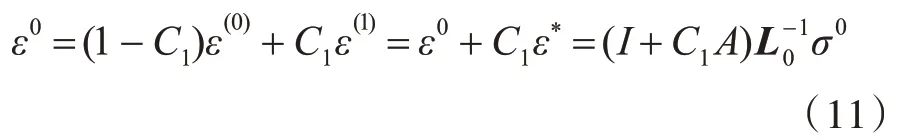
最终得到复合材料的等效弹性模量

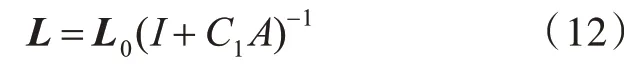
式中，L0，L1和L 的矩阵形式为材料的刚度矩阵C，当材料为各向同性时，刚度矩阵

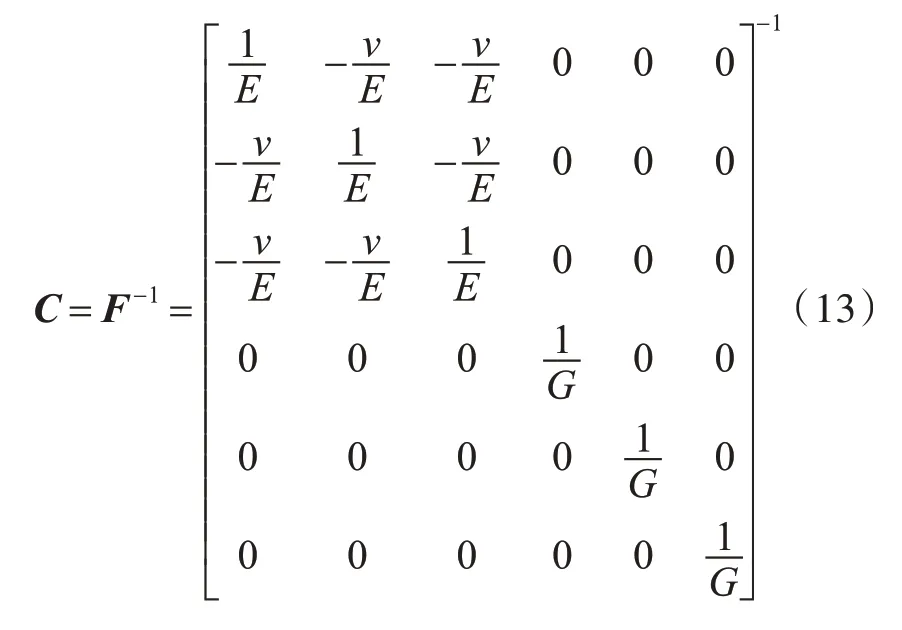
其中，F 为材料的柔度矩阵。

当材料为各向异性时，

求出L 以后，对其求逆得到柔度矩阵，就能较方便地得到各个等效弹性模量。

2 横向增强芯材的等效模量计算

2.1 单胞模型

图1 所示为横向增强夹芯层合板，上、下层为复合材料面板，中间芯材由泡沫基体和圆柱体增强构件组成。

图1 横向增强夹芯层合板示意图Fig.1 Sketch of the transverse reinforced sandwich laminated plate

根据层合板中空间位置分布的对称性和周期性，可以认为它是由一系列单胞（也称代表性体积单元）在厚度平面上排列组成，如图2 所示。单胞由基体和圆柱体夹杂体共同构成，前者一般采用泡沫材料，后者则可以选用树脂柱、纤维柱或者其他材料。

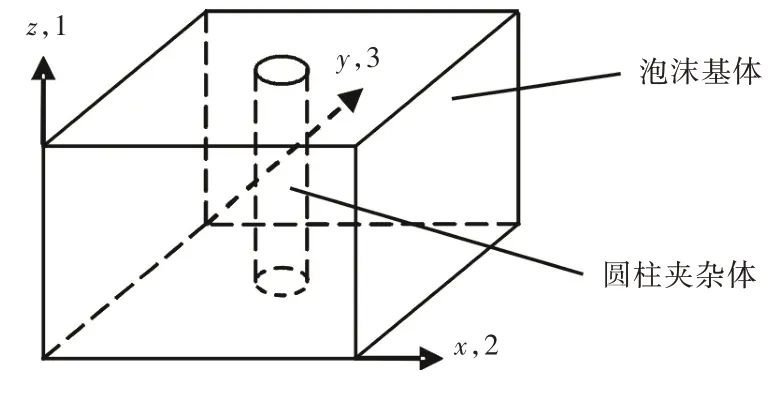
图2 横向增强芯材的单胞示意图Fig.2 Sketch of the unit cell of the transverse reinforced core material

单胞模型的相关参数如表1 所示。

由表中几何尺寸可以确定式（12）中增强相的体积分数

表1 单胞模型参数Tab.1 Parameters of the unit cell model

2.2 有限元模型

复合材料细观力学有限元法是将常规有限元法应用于复合材料细观结构的代表性体积单元上，通过有限元计算获得细观应力和应变场之后，通过均匀化方法计算获得复合材料的等效弹性模量。这种等效的基础是能量等效原理，即在均匀的位移或者力边界条件作用下，代表性体积单元所产生的弹性应变能等同于等效之后的形状和大小都与之完全相同的均质体产生的应变能，然后把该均质体的性能作为所求复合材料的等效性能［10］。

本文利用有限元软件ANSYS 中的SOLID45实体单元建立单胞有限元模型，x 轴和y 轴为长宽方向，即2，3 方向，z 轴为夹杂圆柱体的轴向，即1方向，坐标设置如图2 所示。单胞有限元模型如图3 所示。

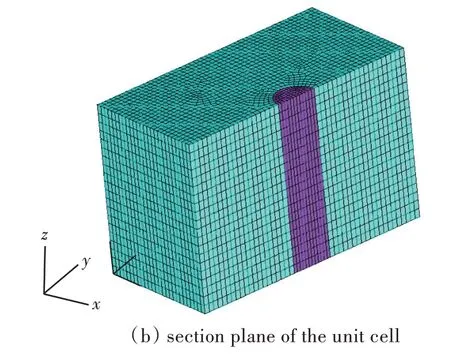
图3 单胞有限元模型Fig.3 The FE model of unit cell

考虑到尺寸足够大的芯材，当其受到轴向和横向拉伸或压缩时，可以认为单胞仍然保持自身的对称性及空间上的周期性，即单胞的各个表面均是对称面。以计算E11为例，单胞有限元模型的边界条件为

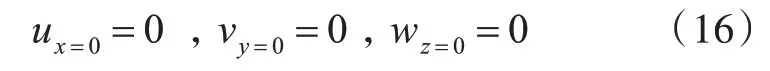
施加位移载荷wz=h=δ，在有限元计算之后，相关应变为

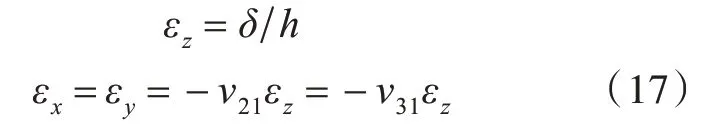
式中，εx和εy为有限元计算所得，并且都是体积平均值。复合材料的体积平均应变和应力分别等于其边界上的平均应变和应力，因此，最终计算都用相关表面上的平均应变和应力代替。提取z=h面上所有节点的节点力之和∑Fz，则单胞z 方向的平均应力为

根据胡克定律，可得

采用类似的边界条件和加载方式，可以得到横向弹性模量E22，E33以及v32。根据芯材的横观各向同性特性，可以计算出面内剪切模量G23=E22/[2(1+v23)]。

2.3 算例验证

按照上述分析，通过两种途径分别验证计算方法的正确性：首先，分别采用Mori-Tanaka 方法和有限元方法对单胞的等效弹性模量计算结果进行验证；而后，进一步建立本文所述的横向增强夹芯板的实际平板结构和等效夹芯板结构，分别计算弯曲性能并进行对比分析。

2.3.1 单胞算例验证

分别采用Mori-Tanaka 理论方法和有限元方法对单胞的等效弹性模量进行计算，计算结果如表2 所示。

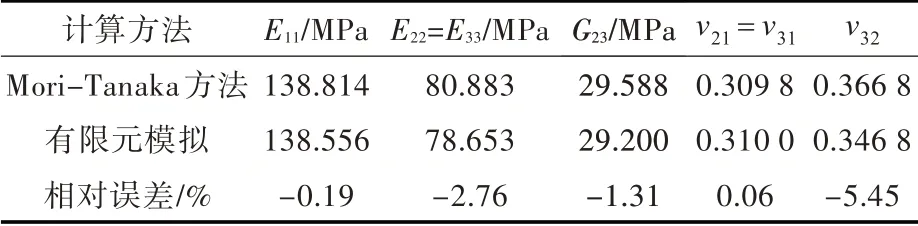
表2 Mori-Tanaka 方法和有限元方法计算结果对比Tab.2 Comparison between results of Mori-Tanaka method and the FEM simulation

由表2 中的数据可看出，采用Mori-Tanaka 方法计算出来的单胞等效弹性模量和泊松比相比吻合较好，最大误差仅-5.45%。造成二者误差的主要原因是：一方面，有限元计算的准确度与网格密度、边界条件的设置是否合适有关；另一方面，Mo⁃ri-Tanaka 方法采用的Eshelby 张量以及许多假设是基于无限大基体的单个夹杂而建立，即夹杂体积分数十分小，因此与单胞模型有差别。从相互验证的角度来看，无论是Mori-Tanaka 方法还是有限元方法，在计算这类带有圆柱体横向增强芯材的等效弹性模量上，准确度均较高。

Mori-Tanaka 方法属理论分析，方法简单易用，但其应用具有一定的限制性。例如，其只能对横向增强构件是球体、椭球体和圆柱体等这类复合芯材进行研究，在增强构件的体积分数过大时，会降低其准确性。而有限元法的适用范围则较广泛，通过建立结构细观模型，其能模拟带有各种复杂形状以及分布形式各异的增强构件复合芯材的应力和应变场，从而计算出结构的等效弹性模量。但这种广泛适用性的另一面又反映了其缺点，即对不同的复合结构，需要有针对性的建模，包括边界条件和载荷的设计等，没有理论方法简便。

2.3.2 夹芯板算例验证

采用ANSYS 有限元软件分析横向增强夹芯板实际结构和Mori-Tanaka 等效夹芯板结构的弯曲力学性能。夹芯板结构尺寸为0.9 m×0.6 m，面板厚0.005 m，芯层厚0.04 m，材料属性为表2 中Mori-Tanaka 方法的计算结果（表中没有给出的G12=G13= 29.84 MPa）。面板和芯层均选用SOL⁃ID45 单元，最小的网格尺度和最大的网格尺度分别约为1.25 mm 和5 mm。实际结构和等效结构有限元模型如4 和图5 所示。

对上述结构进行四边简支约束，底面加载1.0×105Pa 的均布压力，进行静力分析以后，下面将给出部分结果云图。二者的横向位移和y 向正应力云图如图6 和图7 所示。

图4 横向增强夹芯板有限元模型Fig.4 The FE model of transverse reinforced sandwich plate

图5 等效夹芯板有限元模型Fig.5 The FE model of equivalent sandwich plate

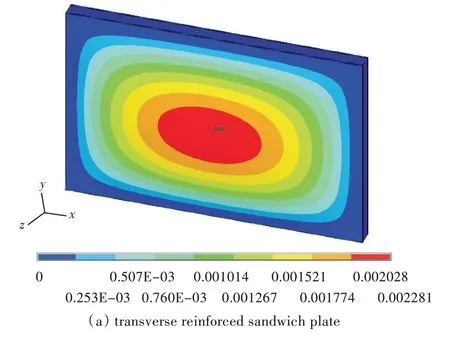
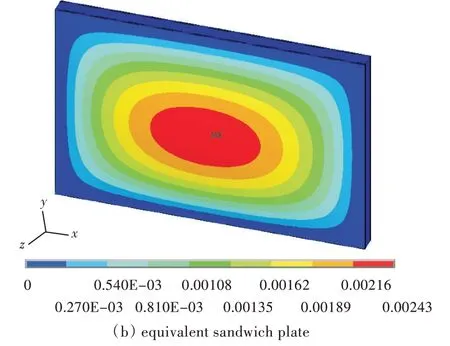
图6 两种模型的横向位移Fig.6 Transverse displacement of the two models

图7 两种模型的y 向正应力Fig.7 Normal stress of the two models in direction y

由云图来看，横向增强夹芯板和等效夹芯板的横向位移云图基本一致，实际模型的最大位移为2.281 mm，等效模型的最大位移为2.43 mm，误差为6.53%。y 向正应力云图的分布也基本一致，横向增强夹芯板的最大y 向正应力为58 MPa，等效夹芯板的则为57.4 MPa，误差为1.03%，上述误差均在可接受范围内。限于篇幅未给出的其他结果基本上也是这样的效果。另一方面，从应力云图来看，由横向增强夹芯板实际模型的结果可以反映出增强结构与基体之间的应力集中情况，而等效夹芯板则由于芯层等效处理变成了均质芯层，因而丢失了应力集中等细节信息。但从整体结果对比来看，本文的Mori-Tanaka 方法具有很大的适用性和准确性，等效模型的计算结果依然能够反映出结构的总体力学性能。

3 相关参数对复合芯材等效弹性模量的影响规律

本节将采用Mori-Tanaka 方法研究基体材料、横向增强支柱材料、单胞尺寸和横向增强支柱直径对整个单胞的等效弹性模量的影响规律。计算的基础模型仍然是前节给出的长宽相等的单胞模型。相关变化参数如表3 所示。

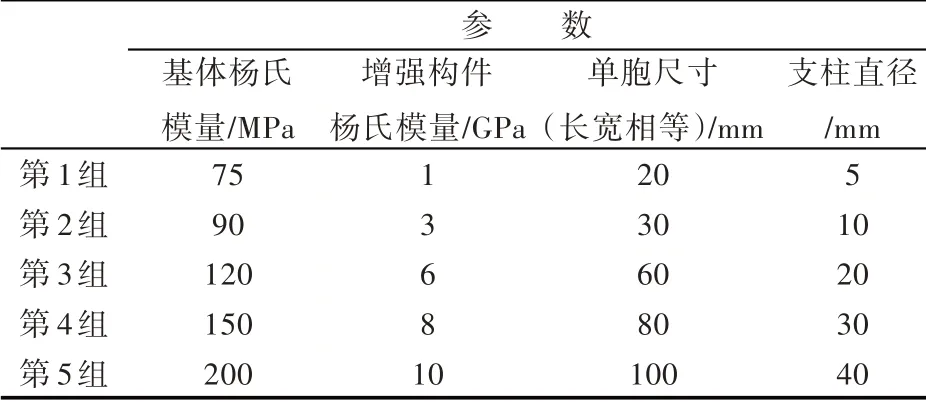
表3 参数变化范围Tab.3 Variation range of the parameters

Mori-Tanaka 方法的计算结果如图8～图11所示。

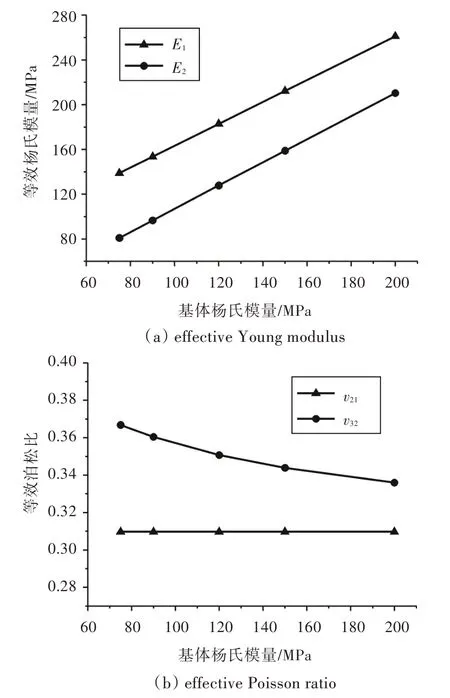
图8 基体杨氏模量对等效弹性模量的影响Fig.8 Effects of Young modulus of the matrix on effective elastic modulus

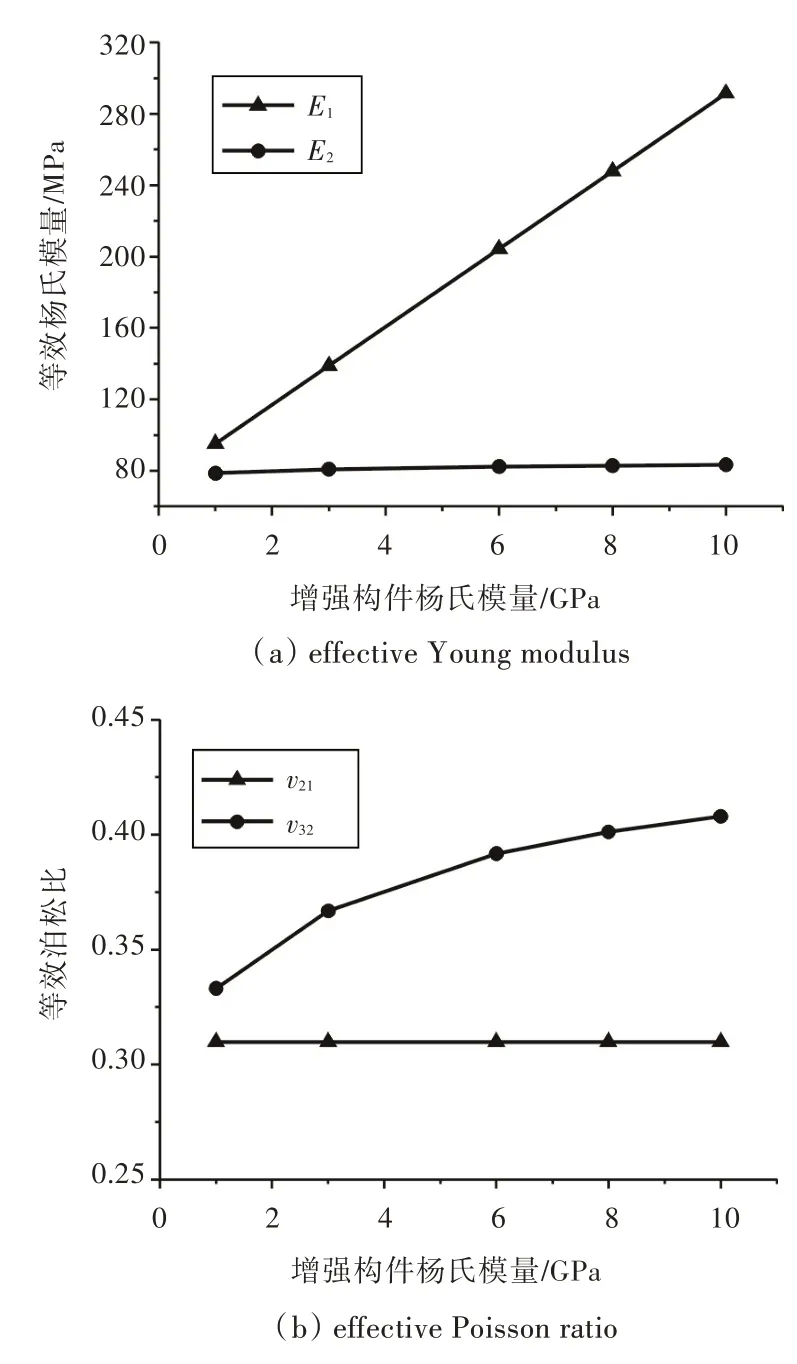
图9 增强构件杨氏模量对等效弹性模量的影响Fig.9 Effects of Young modulus of the reinforced components on effective elastic modulus

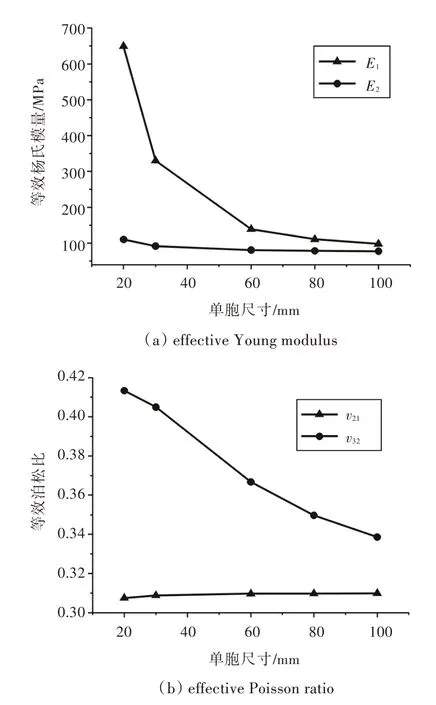
图10 单胞尺寸对等效弹性模量的影响Fig.10 Effects of the size of unit cell on effective elastic modulus

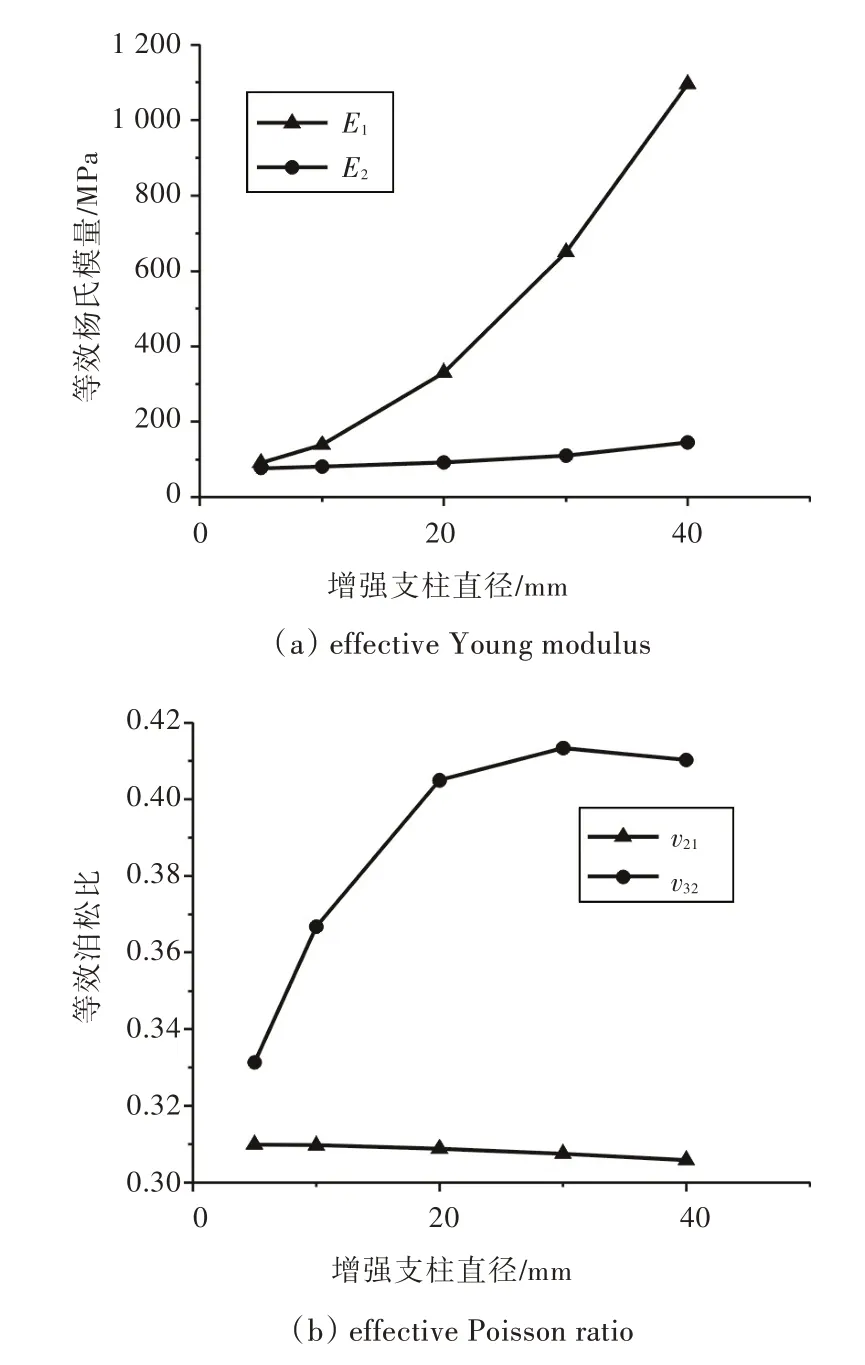
图11 横向增强圆柱直径对等效弹性模量的影响Fig.11 Effects of the diameter of transverse reinforced cylinder on effective elastic modulus

由图8 可看出，随着基体材料杨氏模量的逐渐增大，复合芯材横向（E1）和面内等效杨氏模量（E2）也相应增大，类似于线性增长；面内等效泊松比v32逐渐减小，说明基体杨氏模量的增大抑制了复合芯材的面内泊松效应。而横向等效泊松比v21则基本不受基体材料杨氏模量的影响，几乎保持不变。

由图9 可见，增大横向增强构件的杨氏模量，会使复合芯材的横向等效杨氏模量E1显著增加，但面内等效杨氏模量E2的增加量十分微小。同时，面内等效泊松比v32也相应增大，但随着横向增强构件杨氏模量的继续增大，其增量逐渐变缓，而横向等效泊松比v21则几乎不受影响。

由图10 的曲线可见，随着单胞尺寸的增大，复合芯材的横向等效杨氏模量E1显著降低，但下降速度越来越慢，而面内等效杨氏模量E2则减小得十分缓慢。同时，面内等效泊松比v32也明显减小，而横向等效泊松比v21的变化趋势则相反，呈缓慢增大趋势。

图11 说明随着横向增强圆柱直径的增大，复合芯材的横向等效杨氏模量E1明显增大，而面内等效杨氏模量E2的增加则相对较慢。同时，面内等效泊松比v32是先迅速增大然后又出现缓慢下降的趋势，而横向等效泊松比v21则是逐渐减小。

单胞尺寸的增大和圆柱直径的减小，导致的一致结果是增强构件密度变小，从而在宏观上使复合芯材的等效模量减小。

综合分析发现，横向等效杨氏模量E1和面内等效泊松比v32受表3 中3 个参数（基体杨氏模量除外）的影响，其分别比面内等效杨氏模量E2和横向等效泊松比v21要大一些。这是由于本文中的横向增强构件在厚度方向的弹性性能是由增强构件来保证，整个单胞体现出一种厚度方向的模量要比水平方向显著的结构特点，因此，横向等效模量E1对相关参数变化更敏感。

4 结 论

本文将Mori-Tanaka 方法与有限元方法进行了互相验证，并采用Mori-Tanaka 方法研究了基体和增强构件的材料属性与尺寸参数对复合芯材等效弹性模量的影响规律，得出以下结论：

1）验证了Mori-Tanaka 理论方法的准确性，可以用于预测文中横向增强芯材的等效弹性模量，并且，其在实际横向增强层合板结构的等效模型力学分析中，准确性较高。

2）随着基体材料杨氏模量的增大，复合芯材的等效E1和E2相应增大；等效v32逐渐减小，等效v21则基本不受基体材料杨氏模量的影响。

3）增大横向增强构件的杨氏模量，等效E1会显著增加，E2的增加量则十分微小；等效v32会相应增大但增量逐渐变缓，而等效v21则几乎不受影响。

4）减小增强构件密度在宏观上会使复合芯材的等效样式模量减小，等效v32明显减小，v21则呈缓慢增大趋势。

［1］ZHAO Y H，WENG G J.Effective elastic moduli of rib⁃bon-reinforced composites［J］. Journal of Applied Me⁃chanics，1990，57（1）：158-167.

［2］刘文辉，张新明，张淳源. 微观结构对复合材料弹性有效性能的影响［J］.工程力学，2005，22（S1）：16-20.LIU Wenhui，ZHANG Xinming，ZHANG Chunyuan.Microstructure effect on elastic properties of composites［J］.Engineering Mechanics，2005，22（s1）：16-20.

［3］王兵，冯吉才，李庆飞，等.纤维柱增强泡沫夹芯的等效力学性能研究［J］.哈尔滨工业大学学报，2012，44（3）：29-33.WANG Bing，FENG Jicai，LI Qingfei，et al. Study on the effective mechanical properties of foam core sand⁃wich structure reinforced by fiber composite columns［J］.Journal of Harbin Institute of Technology，2012，44（3）：29-33.

［4］雷友锋，魏德明，高德平. 细观力学有限元法预测复合材料宏观有效弹性模量［J］. 燃气涡轮试验与研究，2003，16（3）：11-15，18.LEI Youfeng，WEI Deming，GAO Deping. Predicting macroscopic effective elastic moduli of composites by micro-mechanics FEM［J］. Gas Turbine Experiment and Research，2003，16（3）：11-15，18.

［5］刘振国，冯志海.三维四向编织复合材料弹性模量数值预报［J］. 北京航空航天大学学报，2000，26（2）：182-185.LIU Zhenguo，FENG Zhihai. Numerical prediction of moduli of 3-D and 4-step braided composites［J］.Jour⁃nal of Beijing University of Aeronautics and Astronau⁃tics，2000，26（2）：182-185.

［6］ESHELBY J D. The determination of the elastic field of an ellipsoidal inclusion and related problems［J］. Pro⁃ceedings of the Royal Society，1957，241：376-396.

［7］ESHELBY J D. The elastic field outside an ellipsoidal inclusion［J］. Proceedings of the Royal Society，1959，243：561-569.

［8］杜善义，王彪.复合材料细观力学［M］.北京：科学出版社，1998.

［9］MORI T，TANAKA K. Average stress in matrix and av⁃erage elastic energy of the materials with misfitting in⁃clusions［J］.Acta Metallurgica，1973，21（5）：571-574.

［10］SUN C T，VAIDYA R S.Prediction of composite prop⁃erties from a representative volume element［J］. Com⁃posites Science and Technology，1996，56（2）：171-179.