最小阻力的参数化船型优化研究

陈文战，陈 伟，杨向晖，邱辽原

1 海军驻上海江南造船（集团）有限责任公司军事代表室，上海201913

2 中国舰船研究设计中心，湖北武汉430064

0 引 言

在船舶水动力设计领域，仿真驱动设计的概念已不再陌生。越来越多的设计人员开始将船型变换方法与CFD 仿真软件相结合来开展船型优化，在摆脱重复迭代的建模及计算工作的同时，还能在短时间内获得较优方案，极大地提高了设计的效率与质量。仿真驱动设计需要解决以下3 个基本方面的问题：

1）船型的自动生成及变换是优化的基础。船型变化方法的好坏可以从其是否能够表征复杂船型、船型是否具有全局变化能力、是否能将船型曲面与船型参数相关联等方面考虑。目前，常用的船型变化方法有数学函数法、叠加扰动面法、移动横剖面法和母型融合法［1］等，这些方法在上述能力方面各有优劣。而基于形状参数的船型参数化方法［2］则是目前最为先进的参数化方法，其实质是通过应变能最小原理生成满足诸如面积、形心、曲线的起点或终点的坐标、斜率、曲率等特定几何要求的、光顺的特征曲线，进而基于NURBS理论，利用蒙皮方法生成光顺的船型曲面。该方法建立了船型性能与船型参数之间的关联，所生成的船型曲面具有较强的适用性。

2）快速而准确的性能评估器是使优化具备可行性的关键。在船型性能优化中，以阻力优化最为常见［3］。目前，优化多采用势流理论与经验公式相结合的方法，在保证结果准确的同时还缩短了计算时间。高精度的数值仿真需要结合近似方法才能应用于优化过程，与势流方法相比，其计算时间仍较长。

3）当需要优化的船型参数较多时，船型参数间的耦合对船型性能的影响非常复杂，设计人员很难判断优化空间的具体形态。因此，寻找合适的优化算法将有助于快速获得较优的方案，提高设计效率。

本文在实现船型参数化建模的基础上，将利用Isight 集成框架构建基于阻力的船型优化模型，并以某舰船船型设计为例，结合不同的优化算法开展进流段区域的船型参数优化，较为直观地建立船型参数与船型阻力之间的关联，为船型设计提供新的技术手段和方法。

1 船型参数化方法

曲面法的出现为基于形状参数的船型参数化打下了技术基础，目前，德国柏林理工大学的Har⁃ries 团队正在从事该方面的研究，已成功开发了相关的参数化建模软件Friendship，并已应用于船型、螺旋桨及涡轮等性能优化中。其船型参数化的建模过程如图1 所示。

图1 参数化船型生成步骤Fig.1 Hull form parametric process

下面，将以横剖线为例简要说明特征曲线与特征参数的关系。如图2 所示，横剖面面积曲线SAC、中纵剖线CPC、设计水线DWL、平底线FOB及甲板边线KNUCKLE 等纵向特征曲线决定了生成横剖面曲线ABCD 所必需的第三类特征参数：横剖面曲线ABCD 上A，B，C，D 四点的坐标；横剖面曲线与纵中剖线、设计水线围成的面积。另外，还可定义C、D 点的斜率及曲率特征曲线。

图2 横剖面曲线建模Fig.2 Generation of section

在横剖面曲线构建中，以A 点为坐标原点，y轴指向右舷，z 轴垂直向上建立坐标系。基于NURBS 的横剖面曲线ABCD 可表示为

式中：曲线参数t（0 ≤t ≤1）定义了曲线的变化范围；di（0 ≤i ≤n）为控制顶点；wi为控制顶点的权因子；Ni，k(t)为第i 个k 次B 样条基函数［4］。则横剖面曲线ABCD 要满足以下约束条件：

其中：(yA，zA)，(yB，zB)，(yC，zC)，(yD，zD)为光顺的横剖面曲线ABCD 上四点的坐标；z′B为；S 为半个横剖面面积；T 为设计吃水，H 为折角线高度；θ 为外漂角。

曲线ABCD 光顺，即使其应变能最小

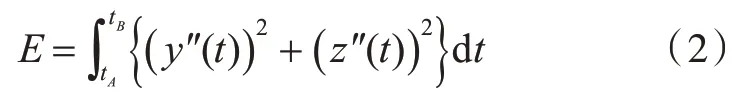
因此，横剖面曲线的参数化设计就转换为使上式最小化的约束非线性规划问题。求解该非线性规划问题，即可获得满足上述约束的、光顺的NURBS 曲线ABCD。

纵向特征曲线的建模方法与横剖面曲线一致。为实现船型参数对船型曲面的驱动，进行特征曲线设计时应尽可能多地增加船型设计常用的参数，如构建设计水线进流段所需的典型船型参数，包括设计水线长Lwl，设计水线宽Bwl，水线面面积系数Cw，漂心纵向坐标Xcf等。但仅凭这几个船型参数还不足以刻画出设计水线的形状，即设计的自由度太大，还需要引入更多的参数约束。为此，将设计水线分成两段，将前、后两段的设计参数与船型参数相关联，使之可以进行协调性调整。如表1 所示，设计水线前、后段面积及形心等参数需要根据船型特征及设计经验进行合理的分配，才能在保证协调的同时减少参数数量，实现典型船型参数的直接驱动。

如图3 所示，定义设计水线的特征参数还包括各段端点处坐标、斜率及曲率等，其他特征曲线的构建方式与此类似。

表1 设计水线与典型船型参数关联Tab.1 Relationship of DWL and parameters

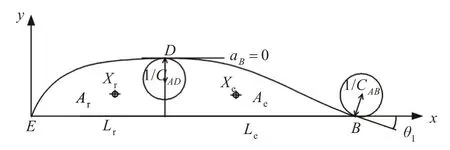
图3 设计水线定义Fig.3 Definition of DWL

生成一组光顺的横剖面曲线簇后，即可利用蒙皮方法生成主船体曲面［5］。

2 基于阻力的船型优化算例

2.1 参数化船型模型

为研究参数化船型优化的可行性，基于上述船型参数化方法，以美国海军LHA 型两栖攻击舰船型为基础，采用仿射变换方式获得了初始的船型方案，并以此方案作为船型参数化的母型。

对船型进行适当简化后所构建的主要纵向特征曲线如图4 所示，艏部船型曲面如图5 所示。

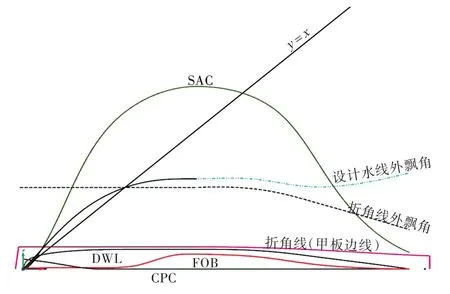
图4 初始方案特征曲线Fig.4 Feature curves of original design

图5 船型艏部曲面Fig.5 Forward surface of parametric hull form

本文开展了给定主尺度及排水量情况下的船型优化。为考察主要船型参数及典型船型特征对船型阻力的影响，选取了以下5 个船型参数作为优化变量，如表2 所示。

表2 船型参数优化变量Tab.2 Optimization variables for hull form design parameters

2.2 阻力计算模型

船型总阻力Rt可表示为

式中，摩擦阻力Rf及粘压阻力Rvp采用Holtrop 方法估算，Rvp+Rf=Rf(1+k)。其中，摩擦阻力系数采用1957年的ITTC 公式计算，形状因子k 采用下式估算：

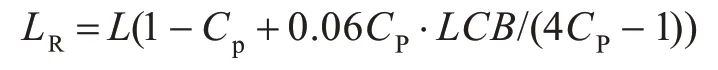
其中LCB 为浮心纵向位置系数。C14是考虑尾部形状的参数，其定义为

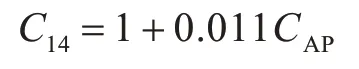
其中，CAP为尾部形状系数，在本文中取为0。

兴波阻力Rw=0.5CwρV2S，其中兴波阻力系数Cw采用边界元法，利用非线性自由面边界条件，由Shipflow 软件计算。为获得较快的求解速度又不失计算结果的准确性，可适当减少船体表面网格划分的数量，采用切波法获得兴波阻力系数［6］。

附体阻力Rapp、空气阻力Ra以及粗糙度补贴ΔCf等可通过设计经验选取。

利用式（3）对上述初始方案进行阻力估算，单位排水量阻力计算结果=0.086 4。

2.3 优化模型

完成各模块的程序编制及数据接口关系规划后，基于Isight 集成框架构建了基于阻力的船型优化模型，实现了船型参数化模块、兴波阻力计算模块及总阻力合成模块的集成。基于Isight 的优化流程如图6 所示。

图6 优化流程Fig.6 Optimization process in Isight

完整的船型优化问题为：

1）优化目标：设计状态总阻力最小，即min Rt。

2）优化变量：典型的船型参数（表2）。

3）约束条件：

（1）在优化过程中，船型、排水量等不发生变化。由于船型是通过参数控制，因此在主尺度及方形系数不变的情况下，这一点可以自动满足。

（2）设计变量约束，表3 给出了各设计变量的取值区间。

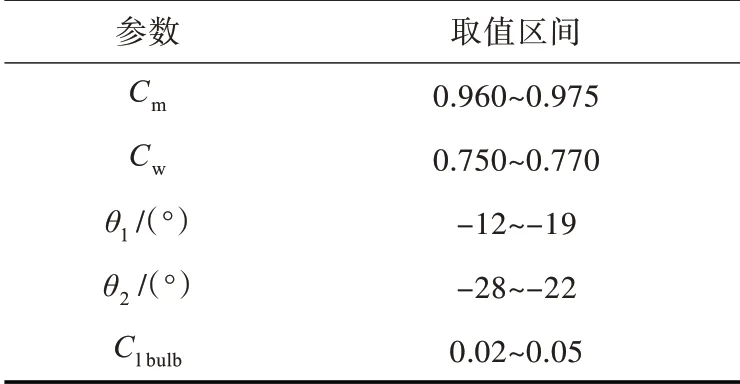
表3 设计变量取值区间Tab.3 Design parameters

4）优化算法。

本优化为单目标优化，设计空间较复杂，呈现出较强的非线性。全局探索方法是求解此类问题的有效途径，但与基于梯度的优化算法相比，全局探索方法的计算量相对较大。为比较各优化算法在参数化船型优化中的适用性，针对该问题，在Isight算法库中选取了3 种优化算法开展研究：

（1）多岛遗传算法（MIGA）：设置子种群的大小为10，种群数为5，代数为10，其他保持默认。

（2）模拟退火算法（ASA）：设置优化运行的最大次数为500，其他参数保持默认。

（3）混合优化算法（Pointer）：主要包括线性单纯形法、序列二次规划法、最速下降法和遗传算法。算法会自动捕捉设计空间的信息，然后灵活地组合算法并形成一个最优的优化策略。初始设置优化的时长为8 h，每次优化的时间约为5 min，其他参数保持默认。

在优化过程中，约束兴波阻力系数的迭代步数处理方法为：对迭代15 步后仍未收敛的方案，程序将认为是失败的方案并予以标记，在后处理中需要剔除。

2.4 优化结果及分析

本文针对上述参数化船型开展了参数优化，图7 所示为总阻力Rt在不同优化算法下的优化历时。由图可见，MIGA 和Pointer 算法对设计空间的适用性要优于ASA，MIGA 和Pointer 算法能较快地确定计算域的峰值区域，而ASA 尽管较早就捕捉到了最优解，但后续目标函数值出现了反复波动，影响了优化的整体效果。

从优化的效率来看，Pointer 算法经过约120次迭代后基本找到了最优解，而MIGA 尽管已经确定了峰值区域，但需要进行多代、大量种群的评价计算，收敛至最优解的过程较慢，效率不高。综合考虑，Pointer 算法兼顾了遗传算法全局搜索能力强和梯度算法速度快的优点，适于多参数、设计空间复杂的优化问题。

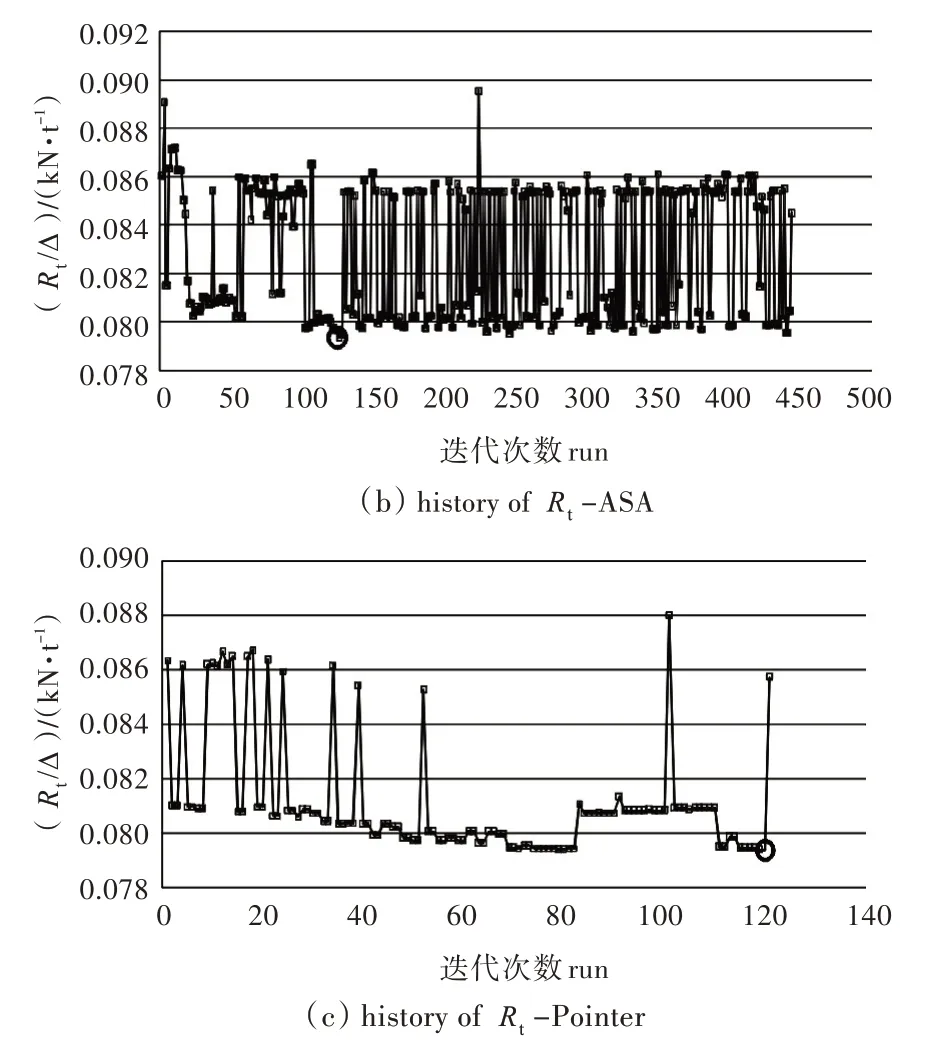
图7 不同优化算法的阻力优化历时Fig.7 Resistance optimization histories by different optimization algorithms

Pointer 算法下各设计参数的优化历时如图8所示。

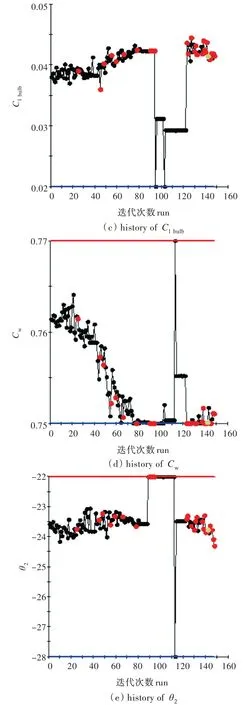
图8 各参数优化历时Fig.8 Parameters optimization histories

各优化算法的最优解如表4 所示，从中可看出优化效果较明显。以Pointer 优化方案为例，总阻力较初始方案下降了约8%。ASA 和Pointer 算法所得最优解的阻力基本接近，系数值略有差异，这也说明了船型参数的搭配对船型性能的影响是很敏感的。另外，对比三组优化结果可以看出，优化参数中对阻力影响最为显著的是设计水线形状，3 个方案所得的水线面系数及水线面进流角基本一致。

表4 参数优化结果Tab.4 Parameters optimization results

优化前、后的船型首部纵剖线形状及特征曲线对比如图9 所示，从中可见优化方案的船型光顺良好。优化结果表明，基于形状参数的船型优化方法在船型设计优化中具有一定的应用潜力及适用性。

3 结 语

图9 船型优化结果Fig.9 Hull form optimization result

本文介绍了基于形状参数的船型参数化基本思路和方法，并以某船型优化为例，阐述了利用Isight 实现基于阻力的参数化船型优化的基本流程。优化结果表明，基于形状参数表达的船型曲面光顺合理，优化效果显著，有利于设计人员直接分析船型参数对船型性能的影响。本文所形成的方法和手段对船型设计具有一定的实用价值。

本文仅针对阻力开展了船型优化研究，而实际上，解决了船型的参数化表达，就能在构建相关航行性能评估器的基础上，从真正意义上实现船型综合航行性能的优化，即船舶航行性能多学科设计优化，后续将在这方面加强研究。

［1］刘祖源，冯佰威，詹成胜. 船体型线多学科设计优化［M］.北京：国防工业出版社，2010.

［2］张萍，冷文浩，朱德祥，等.一种新的船体型线自动光顺方法［J］.船舶力学，2008，12（6）：880-885.ZHANG Ping，LENG Wenhao，ZHU Dexiang，et al. A new automatic fairing approach of hull lines［J］. Jour⁃nal of Ship Mechanics，2008，12（6）：880-885.

［3］邱辽原，谢伟，姜治芳，等. 基于参数化CAD 模型的船型阻力/耐波性一体化设计［J］. 中国舰船研究，2011，6（1）：18-21，29.QIU Liaoyuan，XIE wei，JIANG Zhifang，et al. Integrat⁃ed ship resistence/seakeeping optimization based on parametric CAD model［J］.Chinese Journal of Ship Re⁃search，2011，6（1）：18-21，29.

［4］HARRIES S. Parametric design and hydrodynamic op⁃timization of ship hull forms［D］. Berlin：Technische Universitt Berlin，1998.

［5］HARRIES S，NOWACKI H. Form parameter approach to the design of fair hull shapes［C］// 10th international conference on computer applications in shipbuilding，ICCAS’99.Cambridge，USA，1999.

［6］陈伟，许辉，邱辽原，等. 基于SHIPFLOW 的方尾舰船阻力快速预报研究［J］. 中国舰船研究，2012，7（4）：17-22.CHEN Wei，XU Hui，QIU Liaoyuan，et al. Fast resis⁃tance prediction for ship with transom stern based on SHIPFLOW［J］. Chinese Journal of Ship Research，2012，7（4）：17-22.