最佳相位的多载波QAM

何健标，向潞璐

(深圳技师学院电子通信系通信教研室，广东深圳518000)

视频点播技术(Vedio on Demand，VOD)与被动收看节目的广播电视不同，可根据观众需要随时选择节目。在众多VOD解决方案中，IPQAM方案由于QoS有保证且前期投入小、扩容便利，成为目前国内各运营商的首选［1］。IPQAM的关键是多载波QAM技术，可以在一个物理RF端口输出多个相邻频点的QAM信号。

多载波QAM的设计实现主要分为调制和载波合成两部分。关于调制，文献［2］提出了一种根据CORDIC相位旋转算法减少乘法器数量的实现结构;关于载波合成，常用方法是直接数字频率合成算法［3］(DDFS)，其性能关键在于幅度量化精度和相位量化精度，其中相位量化精度尤其重要［4］，但DDFS所需存储容量会随相位量化精度的增加呈指数增长。

虽然文献［2］提出的实现结构可以减少乘法器，但CORDIC算法是一个多级递归算法，对于高速信号处理(DDFS的主时钟频率都非常高)，CORDIC算法一般只能采用并行多级流水线结构，与之相对应的是多级移位加法器［5］，其结构本质上和乘法器没有太大的区别。目前主流FPGA都在内部集成了性能优越的硬件乘法器模块，文献［2］尤其不适合FPGA实现。实现高精度DDFS的传统方法是利用三角函数对称性压缩存储容量，压缩效果不大;近年来相关的研究都是在利用对称性的基础上，采用CORDIC算法［5］或是各种近似计算法［6-7］实现高精度DDFS的同时大幅度压缩存储需求。但上述方法会引入信号幅度的截入误差，而且需要额外的逻辑资源。

1 多载波QAM模型

假设调制的4个相邻目标频点分别为ω1，ω2，ω3，ω4，而这4个频点的调制信号的I，Q分量分别为I1，I2，I3，I4和Q1，Q2，Q3，Q4，那么这4路的QAM输出信号的总和为

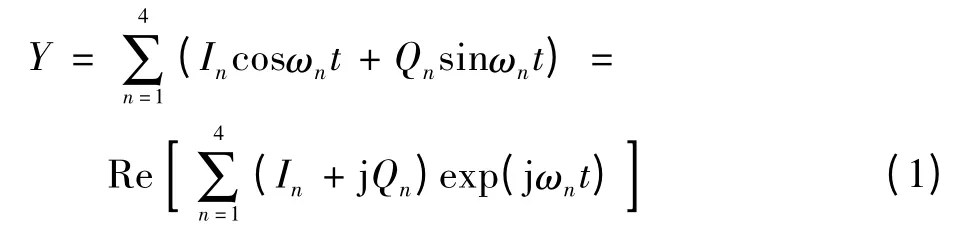
传统设备都是在模拟域完成各个频点QAM信号的合成(如图1)。

图1 模拟域的多频点QAM信号合成

每个频点都需要独立的DAC、上变频器和功放等设备，该方法集成度低、成本高且干扰大。对式(1)进行变换，有

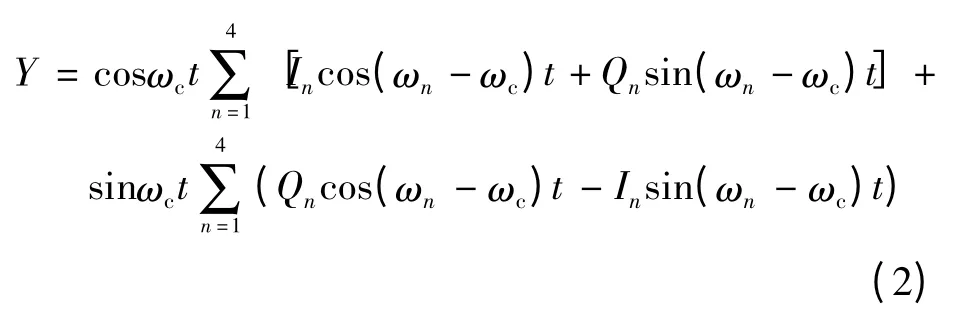
式中:Qncos(ωn-ωc)t-Insin(ωn-ωc)t是Incos(ωnωc)t+Qnsin(ωn-ωc)t的希尔伯特变换。式(2)所表达的物理含义就是将信号In和Qn调制到固定中频(ωn-ωc)，然后再上变频到目标频点的过程(见图2，其中LOn=ωn-ωc)。

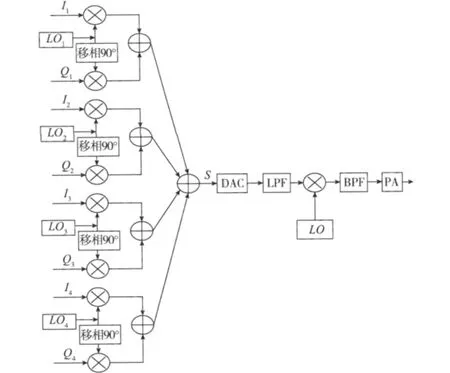
图2 数字域的多载波QAM调制器

固定中频处的多载波QAM为

由于4个目标频点是相邻的，而且中国数字电视的制式规定，相邻频点之间的频率间隔是8 MHz，那么当ωc=时，式(3)可以改写成

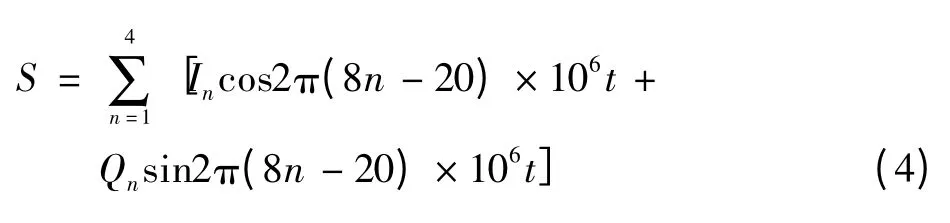
2 最佳相位调制

多载波QAM的输出信号S最终要经过DAC转换为模拟信号(图2)，由于数模转换时数据的截断会引入量化噪声，所以当DAC的量化精度确定后，在数字域提高输出信噪比就要尽可能地提高每个子载波输出信号的电平。

一般而言，S采用N bit的DAC进行量化，每路子载波的I，Q分量信号电平就应分别用(N-3)bit表示。在式(4)中，假设In和Qn的最大值为A(在符号映射过程中，为了控制成形滤波器占用的资源，一般采用5 bit数据进行各种星座的符号映射［8-10］，这样在不同的星座中符号映射的最大值是不一样的，但通过调整成形滤波器系数的比例因子，可以保证每种星座符号映射的最大值相同。所以上述假设总是成立的)，根据三角变换，有

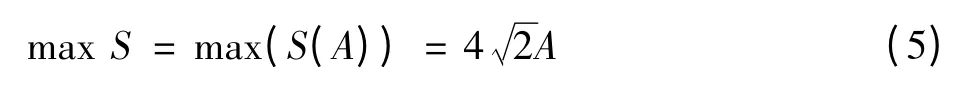
换言之，如果每路子载波的I，Q分量各用(N-3)bit表示，那么DAC输出模拟信号的幅度永远都不会超过DAC满额输出的，这样的数模转换降低了信号的输出功率和输出信噪比。

为尽可能地提高每个子载波的输出信号功率，应使max S对应于DAC的满额输出，即max S=2N-1，其中N为DAC的量化精度。在式(5)中，(max S)/A=为一常数，这个结果对应的是4路QAM调制的载波初始相位相同的常规情况，在最佳相位调制中需要寻找4路QAM调制最佳的相位相对关系。式(4)变成

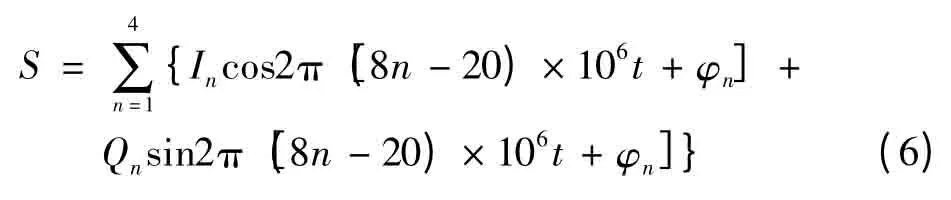
此时(max S)/A不再是一个常数，而是随着相位序列φn而变化。由于max S对应于(2N-1)这个常量，要想调制信号获得最大的输出功率，应使max S和A的比值尽可能的小。使得(max S)/A最小的φn称之为最佳相位序列，最佳相位多载波调制就是通过调整每一路QAM调制载波的初始相位以满足最佳相位序列的要求，使得每个子载波信号获得最大输出功率。

最佳相位序列的求解实质上是一个三角函数的极值求解过程，数学推导繁琐且计算量大。实际工程应用中各子载波的初始相位必然要通过离散化实现，相位序列的组合是有限的，本文利用软件程序自动对所有可能的相位序列进行匹配分析，计算最佳的相位序列，其分析计算过程包括:

1)不失一般性，假设φ1为0，最佳相位序列的物理含义是最佳的载波间相位关系，因此作一般性假设后实际只需求解φ2，φ3，φ4;

2)对2π相位作M点均匀采样后，得到相位采样序列θ，即θ(m)

3)相位抽样序列θ有M个取值，3个载波初始相位φ2，φ3，φ4都分别是M个值之一，因此所有可能的相位序列就是M种可能的3次方组合，共有M3个可能的相位序列，针对所有可能的相位序列逐一计算max S，在M3个max S中最小值所对应的相位序列就是最佳相位序列;

4)M是相位抽样序列θ的取值个数，M越大，相位抽样的精度越高，分析计算得到的最佳相位序列越逼近最优解。当相位抽样的精度足够高时，计算结果会逐步收敛，获得最佳相位序列最优解。

图3是计算机的搜索结果。当相位采样点数M为1，4路子载波的初始相位相同时，(max S)/A=;当相位序列的采样点数M增大，意味着相位序列的采样精度提高，经过分析计算得到的(max S)/A逐渐减小，说明随着M增大，获得的最佳相位序列在逼近最优解;当M取值为16或其倍数时，(max S)/A的值没有变化，同时取得最小值，说明相位序列去16个采样点的情况下已经可以逼近最优解，再增加相位序列的采样精度对改善结果没有帮助。因此，当M等于16时，经计算机全局搜索得到的相位序列φn就是子载波间最佳相位关系。此时，(max S)/A为5.21，若DAC取14 bit量化，即max S对应于0x3FFF，A对应于0x29A5。通过分析计算最佳相位序列，调整各载波的初始相位关系，可使多载波QAM信号获得3.7 dB的信号增益。

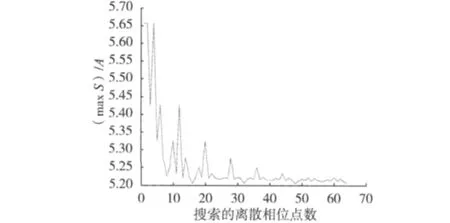
图3 最佳相位的搜索结果

3 分数步进DDS

常规型DDFS之所以由于相位量化精度不足而引入误差，是由于传统的以2的负整数幂作为相位步进而产生的一个周期性的相位截断，而导致频谱的杂散［4］。根据式(6)，待合成子载波的频偏是固定的(4 MHz和12 MHz)，摒弃2的负整数幂换以一个特定分数作为DDFS的相位步进，使4 MHz和12 MHz这两个信号的合成不存在相位截断，那么合成信号就只存在幅度截入误差而不存在相位截断误差，所以采用分数步进型DDFS合成子载波可使信号质量大为改善。

多载波QAM调制器中的DAC经过比较，选择14 bit幅度量化精度、采样率为200 MHz的DAC。即DDFS的系统时钟为200 MHz，要合成4 MHz和12 MHz的信号，对应的分数相位步进应取4/200和12/200，故分数相位步进的DDFS的输出序列分别为

分数步进型DDS需要保存的相位-幅度采样点是50个。根据第2节的分析，每个子载波的信号电平不会超过0x29A5，即每个子载波调制的最终输出的有效位数不会超过12 bit，但考虑到末位计算的精度，DDFS的输出信号采用13 bit的幅度量化。采用特定的分数相位步进，可使子载波合成实现电路的复杂度大大降低。

1)为了保证频率控制的精度，通常DDFS的相位累加器是一个位宽较大(一般取32 bit)的加法器，这是相当复杂的组合电路，在FPGA中组合电路是基于LUT(Look-up Table)结构来实现的，而单个LUT只能作5输入组合电路，复杂的组合电路是通过多级LUT级联来实现的。因此在FPGA中实现大规模组合电路不但耗费大量的LUT，而且还占用庞大的布线资源(Interconnects);而分数相位步进型DDFS直接按照相位步进来存储数据，不需要复杂的相位累加器作为ROM的输入地址，可直接采用一个模50的加1计数器作为ROM的地址发生器。由于加1计数器是常用的数字逻辑器件，FPGA中有专门为实现加1计数器进行优化的电路，以计数器替代原来的加法器作为相位累加器，逻辑资源消耗大为减少而工作性能更加出色。

2)常规型DDFS在相位精度较高时，相位-幅度转换往往要占用巨大的逻辑资源。采用分数相位步进型DDFS，需要保存的相位-幅度转换采样点只有50个，无须压缩，可直接保存。表1比较了分数相位步进型DDFS和Altera公司根据各种优化算法提供的DDFS的IP核占用逻辑资源的情况(DDFS的幅度，相位均采用13 bit量化)。显然，无论采用何种优化算法，Altera提供的IP核所耗用的逻辑资源都远远大于分数相位步进型DDFS模块。

表1 各种DDFS实现方法的资源消耗对比

3)最佳相位多载波QAM合成子载波必须满足最佳相位序列的约束关系。如果是常规型DDFS，必须在每个子载波各自的相位累加器上叠加一个不同的初始相位，以保证子载波间的相对相位关系;而分数相位步进型DDFS则可以在计算相位-幅度转换的采样点时考虑最佳相位的约束关系(式8)，从而使所有子载波可以共用一个模50的加1计数器作为相位累加器，省略了7路相位累加器所耗用的逻辑资源。

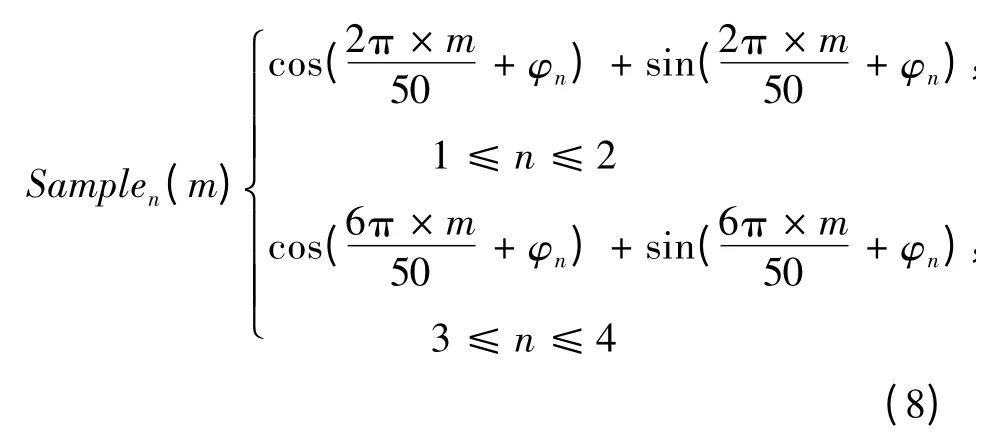
4 实现与仿真

根据上述分析，整个多载波QAM调制芯片的电路实现如图4所示，4路子载波的正余弦分量由8个分数步进型DDFS实现，这8个分数步进型DDFS共用一个模50的加1计数器作为相位-幅度转换模块的地址发生器。

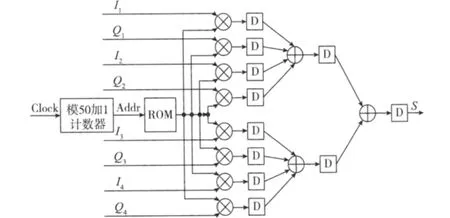
图4 多载波QAM调制芯片实现框图

相位-幅度转换模块由ROM实现，ROM保存了8个DDFS中含有最佳相位约束关系的相位-幅度换算关系，此ROM的数据存储分布为104 bit(13 bit×8)×50，共需要5 200 bit的存储空间。ROM中每一个单元数据(104 bit)定义为

为了更好地比较分数步进型DDFS和其他常规类型DDFS的性能，图5和图6分别给出采用直接型DDFS和分数步进型DDFS合成4 MHz和12 MHz信号的频谱，由于CORDIC和各种近似计算法［5-7］存在计算的截入误差，性能不如直接型DDFS，所以没有参与比较。

根据图5、图6中MATLAB仿真结果显示，无论是4 MHz还是12 MHz的信号合成，随着相位量化精度的提高，直接型DDFS输出信号的频谱杂散逐步得到改善，但即便是相位精度为13 bit的直接型DDFS，其性能仍不如分数相位步进型DDFS。

表2是采用频谱分析仪和矢量信号分析仪对传统多载波QAM信号和最佳相位多载波QAM信号测试的结果。相比之下，经过最佳相位调制算法改进的多载波QAM信号不但在同等条件下增加信号的输出功率，相对于不变的量化噪声功率，提高了输出信噪比，同时采用分数相位步进不仅使得各子载波的频谱杂散现象得到了有效的抑制，而且使各子载波具备了更高的IQ相位精度，因此最佳相位的多载波QAM输出信号在载噪比、带外抑制比、调制误差度等所有测试指标上都得到了明显的改善。

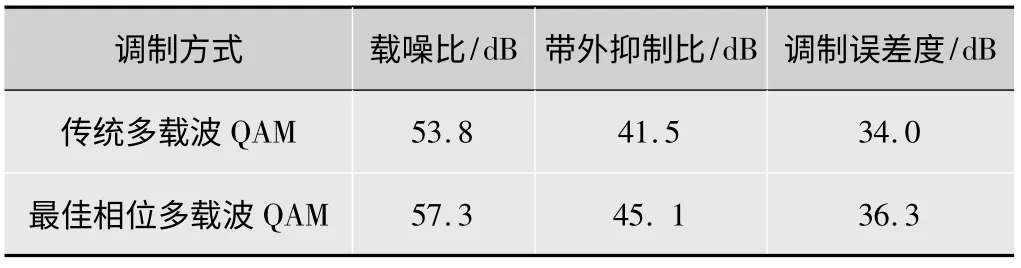
表2 两种多载波QAM的测试指标

［1］陈勇，商彬.IPQAM设备关键技术的研究［J］.电视技术，2008，32(1):122-124.

［2］VANKKA J，KOSUNEN M，SANCHIS I，et al.A multicarrier QAM modulator［J］.IEEE Circuits and Systems，2000，47(1):1-10.

［3］王利众，费元春，郭德淳，等.用DDS技术设计HDTV选台电路［J］.电视技术，2003，27(3):57-75.

［4］李海松，张奇荣，权海洋.DDS的相位截断及相应的杂散信号分析［J］.微电子学与计算机，2006(2):141-143.

［5］刘晨，王森章.直接数字频率合成器的设计及FPGA实现［J］.微电子学与计算机，2004(5):63-65.

［6］WANG C-C C，SHE H-C，HU R.A ROM-less direct digital frequency synthesizer by using trigonometric quadruple angle formula［C］//Proc.9th International Conference on Electronics，Circuits and Systems.［S.l.］:IEEE Press，2002:65-68.

［7］ASHRAFI A，PAN Z，ADHAMI R，et al.A novel ROM-less direct digital frequency synthesizer based on Chebyshev polynomial interpolation［C］//Proc.36th Southeastern Symposium on System Theory.［S.l.］:IEEE Press，2004:393-397.

［8］赵民建，袁梦涛，李式巨，等.全数字多星座图、可变符号率QAM调制器［J］.电路与系统学报，2001(1):1-6.

［9］包莉娜，梁坚，易志强，等.DVB-C映射电路的设计［J］.电子技术，2003(8 ):33-35.

［10］王国正，赵利.一种星座可变的自适应QAM调制方案［J］.电视技术，2012，36(9):92-95.