用DSC曲线数据估算硝化棉的CnB和表观经验级数自催化分解反应热爆炸临界温升速率

姚二岗，胡荣祖，赵凤起，张 海，王 尧，常象宇，高红旭，赵宏安

（1.西安近代化学研究所燃烧与爆炸技术重点实验室，陕西 西安710065；2.西北大学数学系／数据分析和计算化学研究所，陕西 西安710069；3.西安交通大学信息科学与系统科学研究所，陕西 西安710049；4.西北大学信息科学与工程学院，陕西 西安710069）

引 言

放热分解反应体系热爆炸的临界温升速率（dT／dt）Tb是评价含能材料安定性和安全性的重要参数。在估算这个参数方面，胡荣祖等［1-2］推导出一级自催化和表观经验级数自催化分解反应体系（dT／dt）Tb估算式的导出途径；宁斌科、张海等［3-7］估算了NC（11.92% N、12.97%N、13.54%N、13.86%N、14.14%N）（均为质量分数）一级自催化分解反应体系的（dT／dt）Tb值。本工作作为文献［1-7］的拓展，报道n级自催化反应（CnB）热爆炸（dT／dt）Tb估算式的导出途径和NC（14.14% N）的CnB和表观经验级数自催化分解反应（dT／dt）Tb值的估算结果。

1 实 验

1.1 试 样

硝化棉（NC），氮质量分数14.14%，西安近代化学研究所。

1.2 仪器和实验条件

上海天平仪器厂CDR-1型差示扫描量热仪，气氛为静态空气，参比物为α-Al2O3，试样量为0.5mg，走纸速率20mm／min，升温速率为1、2、5、10、20K／min，实际升温速率按照50℃至反应终止温度范围内实际的温升速率计算。

2 理论和方法

单位时间内含能材料热分解放出的热量q1为：

式中：Q为热分解反应的焓，J／mol；V为含能材料的装填体积，cm3；d为装填密度，g／cm3；M为含能材料的摩尔质量，g／mol；dα／dt为自催化反应速率：

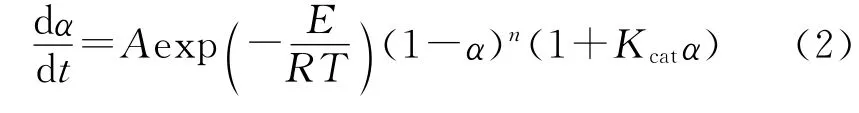
联立方程（1）和（2），得：

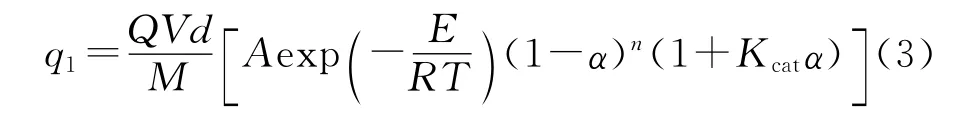
同时，单位时间内因传热由反应区通过器壁向四周环境散失的热量q2为：

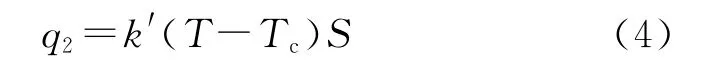
式中：k′为传热系数，J·cm-2·K-1·s-1；S表示药柱表面积，cm2；Tc为按照线性关系Tc=T0+βt确定的反应器壁和空间温度；β为线性加热速率，K／min；T0为热分析曲线离开基线的温度，K。

热爆炸发生时，方程（3）变为：

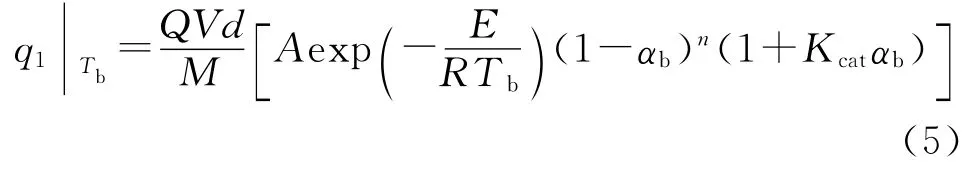
式中：αb为相应于Tb时的α值；Tb为含能材料的热爆炸温度，K。

方程（4）变为：

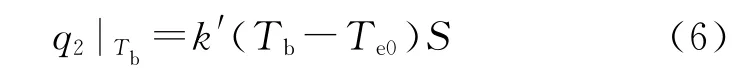
式中：Te0为β→0时的onset温度。

根据q1-T、q2-T关系，热分解过渡到热爆炸的充分必要条件式为：

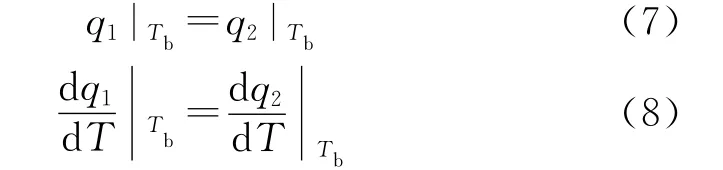
方程（3）对T微分，得：

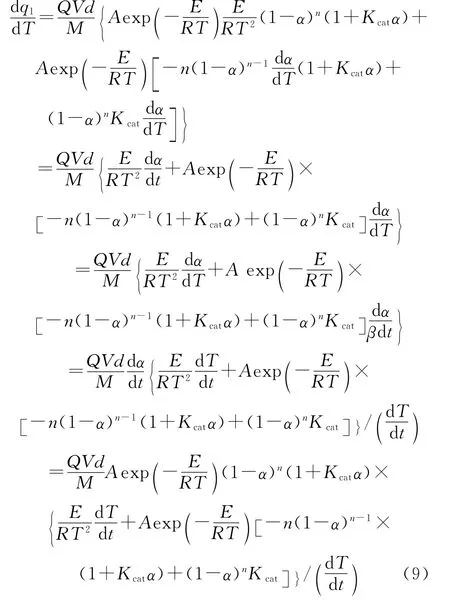
热爆炸发生时（T=Tb），方程（9）变为：

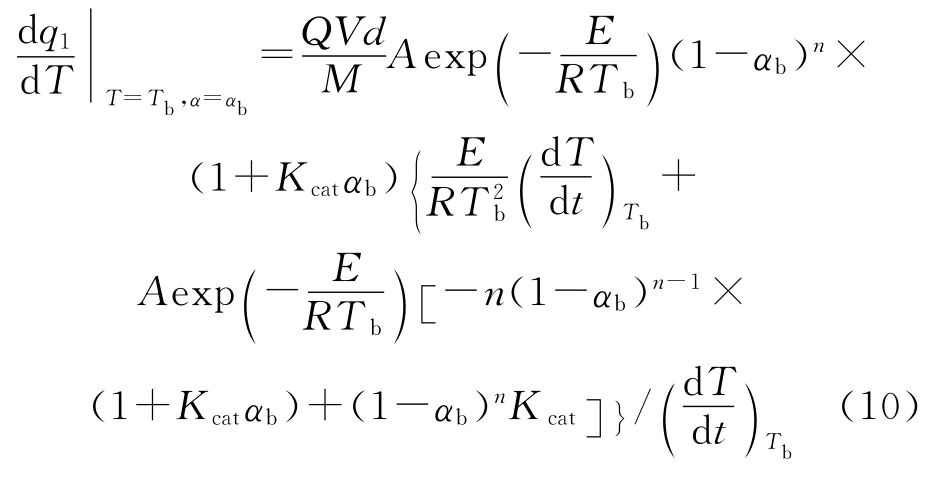
式中：（dT／dt）Tb为热分解转向热爆炸时含能材料中的临界温升速率。

方程（4）对T微分，得：

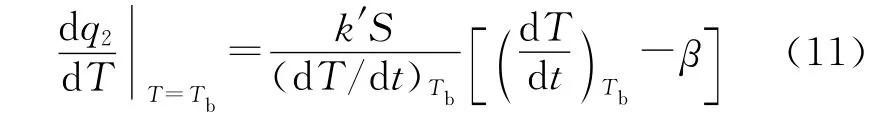
方程（5）、（6）和（7）联立，得：

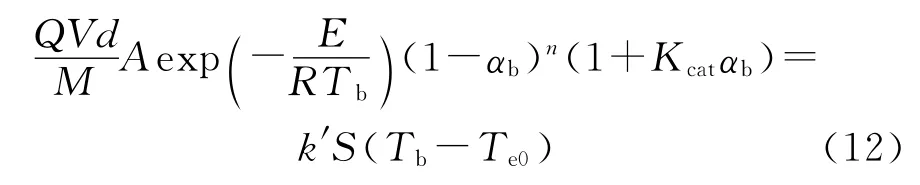
方程（8）、（10）和（11）联立，得：

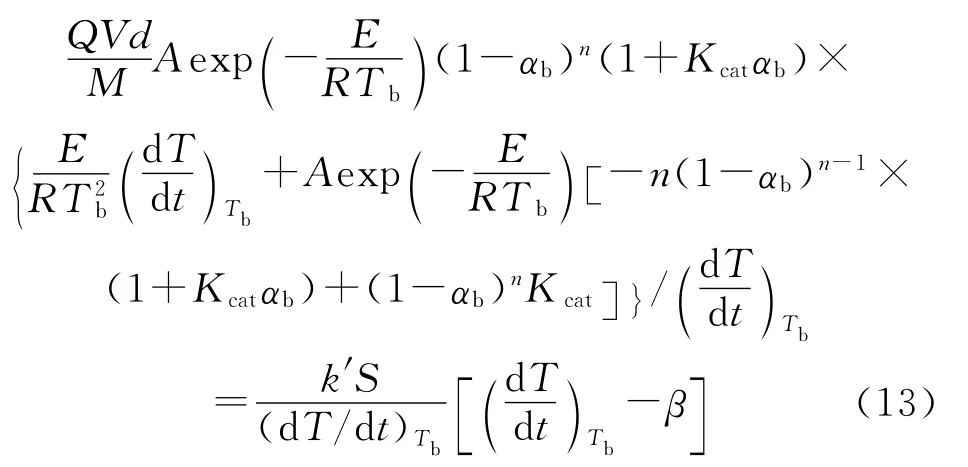
热爆炸开始时，（dT／dt）Tb＞＞β，方程（13）可简化为：

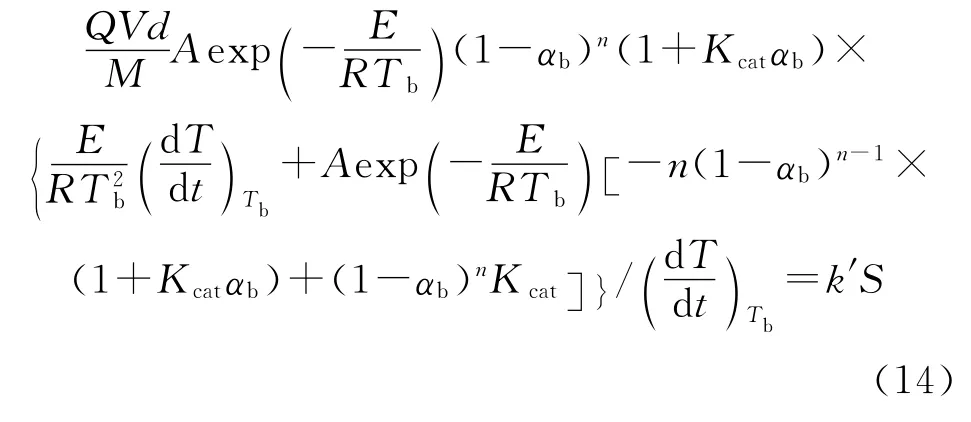
方程（12）和（14）联立，得：

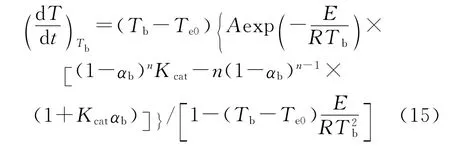
方程（15）为CnB 分解反应转向热爆炸时的临界温升速率式。

一旦从热流曲线解得E、A、n、Kcat、Tb和Te0，就可从方程（15）得到（dT／dT）Tb的值。

同理，对经验级数自催化分解反应速率：

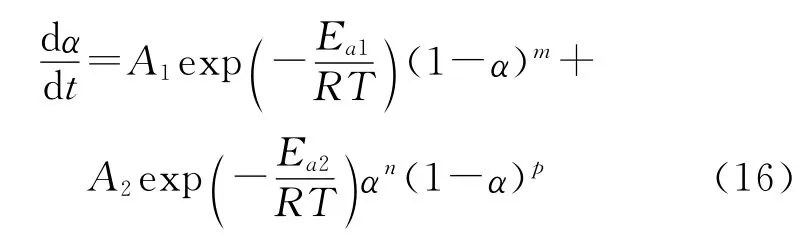
则有：

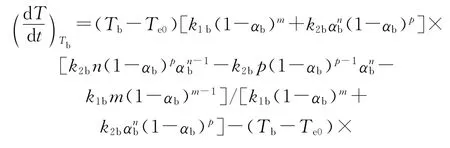
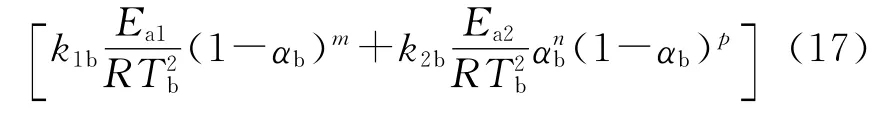
方程（17）称表观经验级数自催化分解转向热爆炸时的临界温升速率式。

一旦从热流曲线解得Ea1、Ea2、A1、A2、Te0、Tb、αb、m、n和p，就可从方程（17）得到（dT／dt）Tb的值。

为求方程（2）中的4个参数（E、A、n、Kcat）和方程（16）中的7个参数（Ea1、Ea2、A1、A2、m、n、p），用具有边界约束非线性优化问题的信赖域方法［8］进行了求解。

给定试验数据：

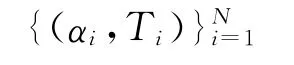
得ti=（Ti-T0）／β，i=1，2，…，N及（dα／dt）i≈（αi-αi-1）／（ti-ti-1），i=1，2，…，N，通过最小化均方误差估计4 参数和7 参数，得到非线性优化模型：

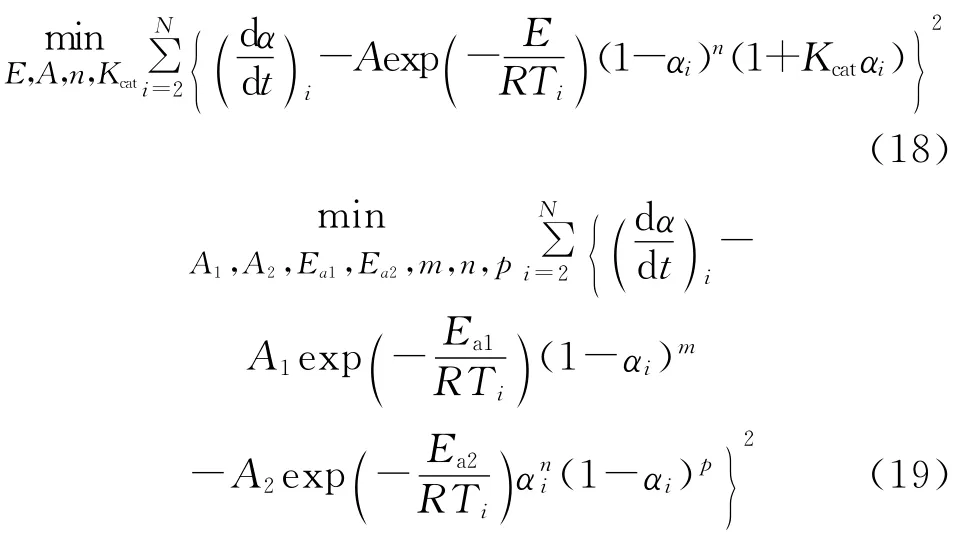
此处，R=8.314J·mol-1·K-1。

为更准确地估算参数，限制参数范围，将公式（18）和（19）分别改写为：

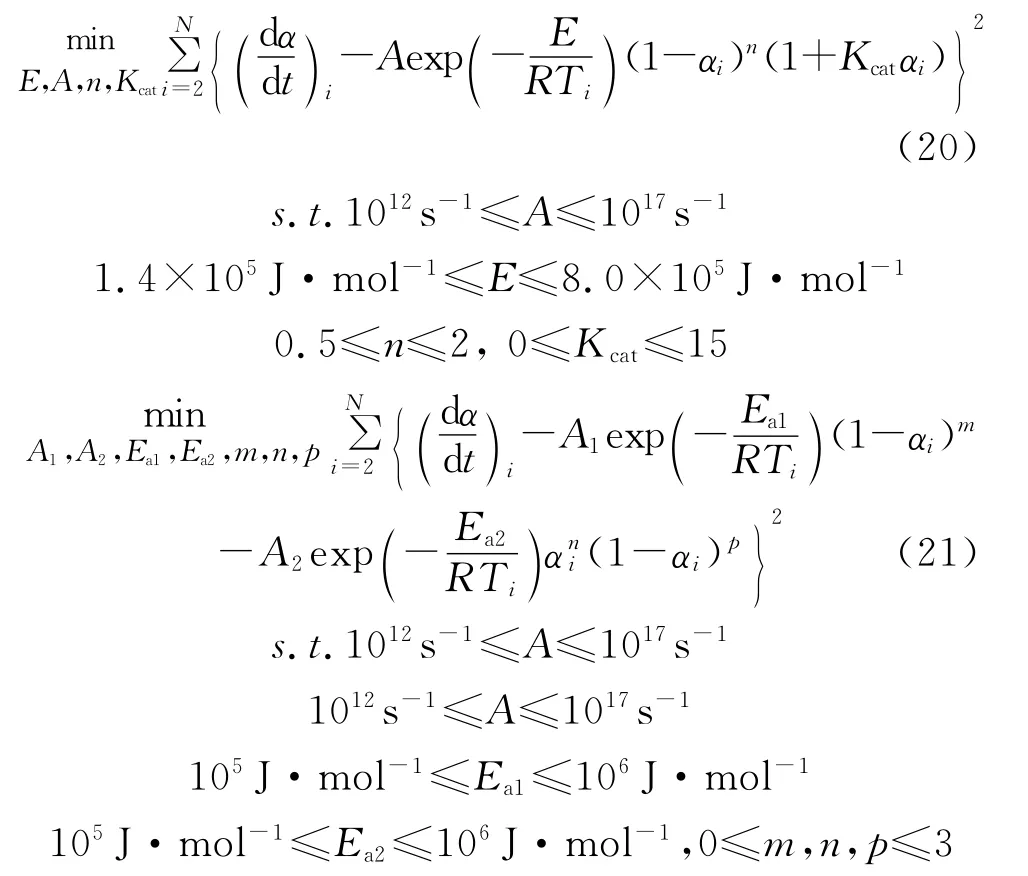
为了叙述简便，具有边界约束的非线性优化问题重新描述为：

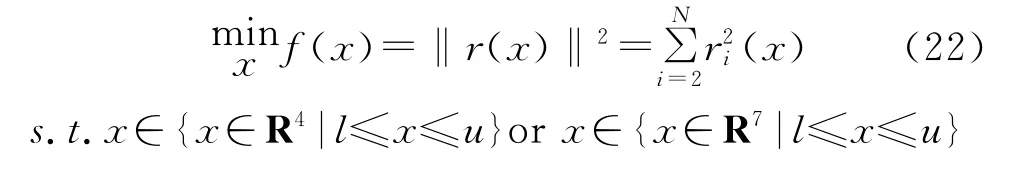
式中：

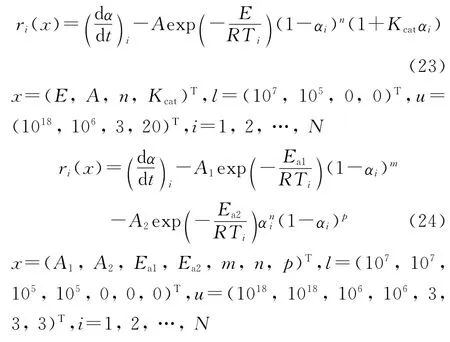
定义可行集Φ≜｛x：l≤x≤u｝及其严格的内部为

根据信赖域方法［8］，定义向量函数v（x）：R4→R4：

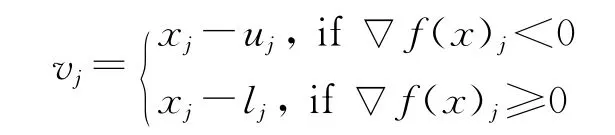
另外，定义矩阵D（x）为，即，D-2是一对角矩阵且其第i个对角元素为｜vi（x）｜。考虑非线性方程组：

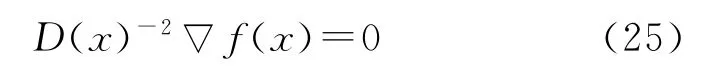
设xk∈int（Φ），式（21）的牛顿迭代满足

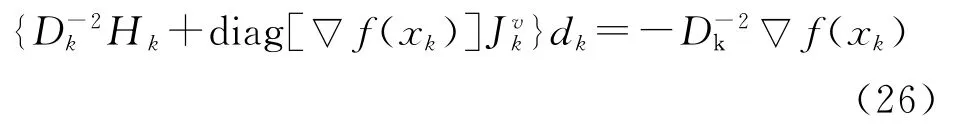
式中：Jv（x）=diag［sgn（▽f）］∈R4×4；Jv（x）=diag［sgn（▽f）］∈R7×7，其作用相当于｜v（x）｜的Jacobian矩阵；梯度g（x）≜▽f（x）；B（x）为Hessian矩阵H（x）≜▽2f（x）的近似解，在此基础上定义二次优化问题：

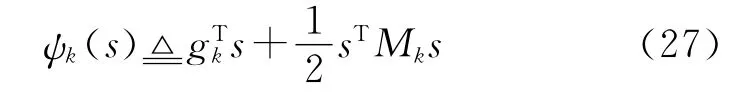
式中：M（x）≜B（x）+C（x）；C（x）≜D（x）diag［g

可以证明，xk是式（22）的局部最小值点，当且仅当sk是下式的解：

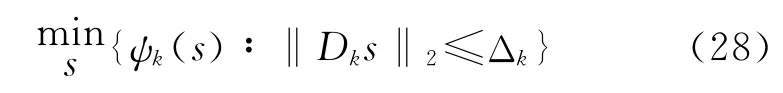
这里，Δk为正数，表示信赖域的大小。因此，可通过求解子问题（28）来确定xk是否为目标函数的最小值点，进而，当信赖域的大小Δk足够大时，局部最小值的邻域中式（25）的牛顿迭代正好是信赖域子问题（28）的解。

解决具有边界约束的非线性优化问题的信赖域方法模型为：

取x0∈int（Φ），循环k=0，1，…

（1）计算f（xk）、gk、Hk及Ck；

（2）根据式（28）计算sk且满足xk+sk∈int（Φ）。

（5）修正模型ψk，矩阵Dk及信赖域大小Δk。

信赖域大小Δk的修正为：给定0＜μ＜η＜1，γ1＜1＜γ2及0＜Λl

若Δk＞Λl时，令Δk+1∈［γ1Δk，Δk］或［Δk，γ2Δk］；

否则，令Δk+1∈［Δk，γ2Δk］。

3 计算实例

用DSC测得高氮量硝化棉（14.14% N）放热分解反应的T-α和β-Te关系数据，见表1 和表2。

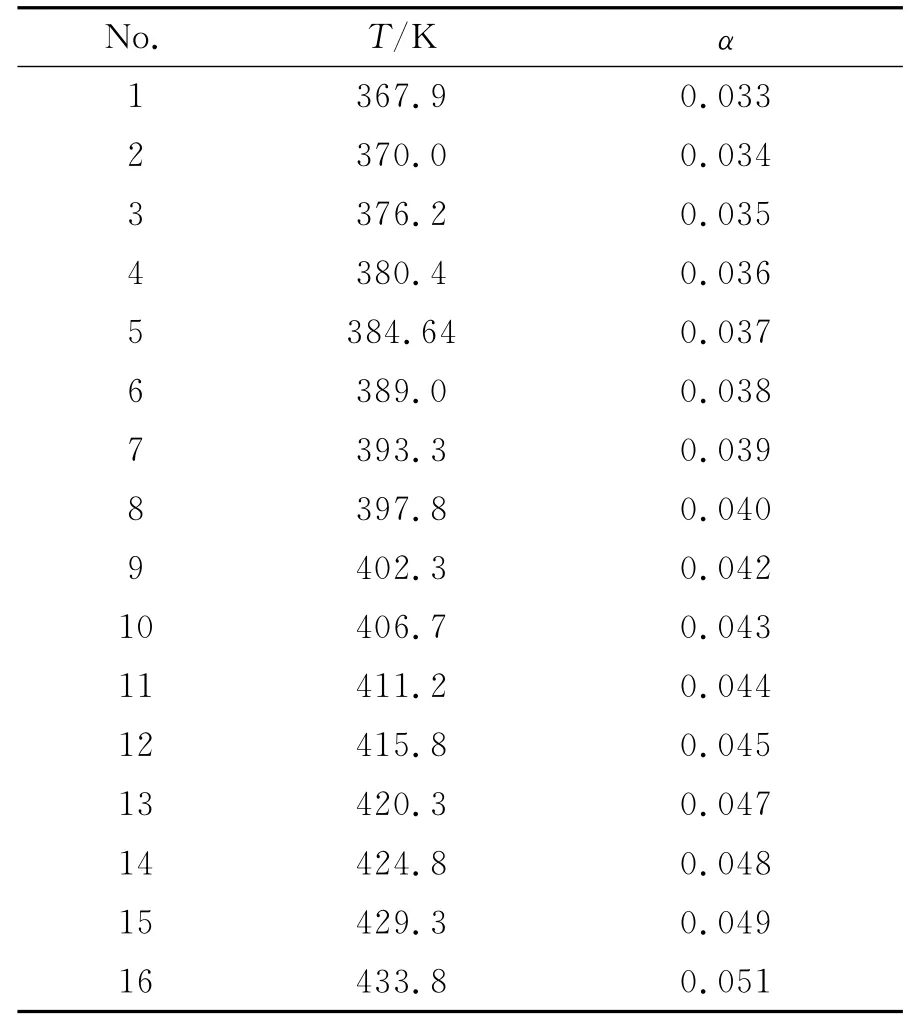
表1 用DSC测得的NC的热分解数据Table 1 Thermal decomposition data of NC determined by DSC

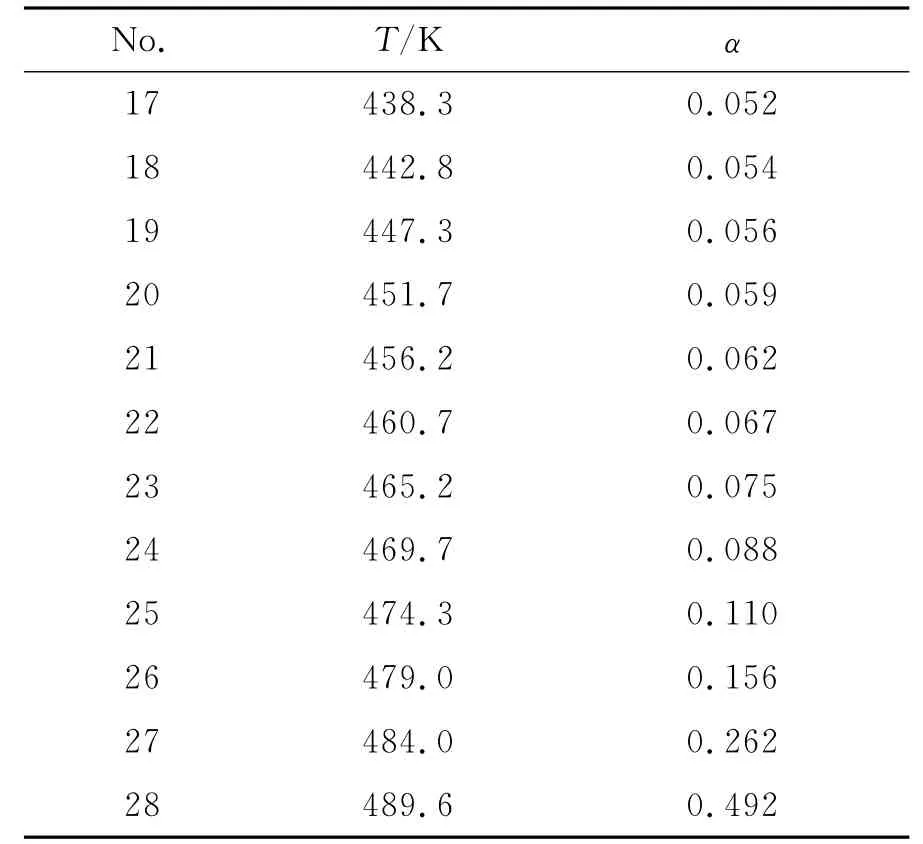
续表1

用方程（2）和（16）分析表1和表2中的数据，得到表3中CnB 和表观经验级数自催化分解反应的动力学参数。在这两个方程中，其计算值与实验值（见表1）的相对误差（Δδ）分别为：0.089和0.060，由方程（15）和（17）获得相应的（dT／dt）Tb值分别为0.073K／s和0.060K／s。根据相对误差最小的原则，认为采用表观经验级数自催化反应速率方程描述NC（14.14%N）的热分解过程是可取的，热分解转向热爆炸时的（dT／dt）Tb值为0.060K／s是可接受的。

表2 NC（14.14% N）热爆炸临界温度（Tb）的计算值Table 2 Calculated values of the critical temperature（Tb）of thermal explosion for NC（14.14% N）

表3 用方程（2）和（16）分析表1和表2中数据的结果Table 3 Results for analyzing the data in Tables 1and 2by Eqs.（2）and（16）

4 结 论

（1）采用非线性约束优化问题的信赖域方法，从非等温DSC曲线数据获得了NC（14.14% N）的n级自催化分解反应（CnB）和表观经验级数自催化分解反应的动力学参数和动力学方程，并获得了其相应的热爆炸临界温升速率值。

（2）非等温条件下NC（14.14% N）热分解过程可用表观经验级数自催化反应动力学方程描述：

dα／dt=1015.76exp（-1 708／RT）（1-α）0.95+1015.76exp（-1 591／RT）α1.81（1-α）1.16

（3）NC（14.14% N）自催化分解过渡到热爆炸时的临界温升速率值为0.060K／s。

［1］胡荣祖，高胜利，赵凤起，等.热分析动力学［M］.北京：科学出版社，2008.

HU Rong-zu，GAO Sheng-li，ZHAO Feng-qi，et al.Thermal Analysis Kinetics［M］.Beijing：Science Press，2008.

［2］胡荣祖，张海，夏志明，等.含能材料放热分解反应体系热爆炸的临界温升速率估算式［J］.含能材料，2003，11（3）：130-133.

HU Rong-zu，ZHANG Hai，XIA Zhi-ming，et al.Estimation formulas of the critical rate of temperature rise for thermal explosion of exothermic decomposition reaction system of energetic materials［J］.Chinese Journal of Energetic Materials，2003，11（3）：130-133.

［3］HU Rong-zu，GUO Peng-jiang，SONG Ji-rong，et al.Estimation of the critical increase temperature rate of thermal explosion of nitrocellulose using non-isothermal DSC［J］.Chinese Journal of Explosives and Propellants，2003，26（2）：53-57.

［4］NING Bin-ke，HU Rong-zu，ZHANG Hai，et al.Estimation of the critical rate of temperature rise for thermal explosion of autocatalytic decomposing reaction of nitrocellulose using non-isothermal DSC［J］.Thermochimica Acta，2004，416（1-2）：47-50.

［5］HU Rong-zu，GUO Peng-jiang，GAO Sheng-li，et al.Estimation of the critical rate of temperature increase of thermal explosion of nitrocellulose using non-isothermal DSC［J］.Chinese Journal of Polymer Science，2003，21（3）：285-289.

［6］GUO Peng-jiang，HU Rong-zu，ZHANG Hai，et al.Estimation of critical rate of temperature rise for thermal explosion of first order autocatalytic decomposition reaction systems by using non-isothermal DSC［J］.Chemical Research in Chinese Universities，2004，20（2）：163-165.

［7］ZHANG Hai，XIA Zhi-ming，GUO Peng-jiang，et al.Estimation of the critical rate of temperature rise for thermal explosion of first-order autocatalytic decomposition reaction systems using non-isothermal DSC［J］.Journal of Hazardous Materials，2002，94（3）：205-210.

［8］Coleman T F，Li Y Y.An interior trust region approach for nonlinear minimization subject to bounds［J］.SIAM Journal on Optimization，1996，6（2）：418-445.

［9］Ozawa T.A new method of analyzing thermogravimetric data［J］.Bulletin of the Chemical Society of Japan，1965，38（1）：1881-1886.