综合确定指标权重的模糊贴近度信任评估
2013-01-21左双勇王祥玲
左双勇,王祥玲
(1.广东培正学院 基础部,广东 广州 510830;2.广州大学华软软件学院 基础部,广东 广州 510990)
在开放的网络环境下,随着各种网络功能的不断完善,数量众多的动态用户使网络世界呈现出社会化的趋势,用户不再是一个个相互孤立的个体,而是依托一定的网络应用,形成了错综复杂的网络人际关系,一个用户可以通过网络直接与成千上万的用户进行交互.由此,基于传统的注册、认证和鉴权的安全机制已经无法满足众多网络应用的要求,需要一种更加灵活的安全机制,这就是基于信任的安全机制.随着P2P网络、网格计算、分布式网络等技术的发展,进一步促进了对如何在网络上建立一套可信模型及相关信任度算法的研究[1].
文献[2]和文献[3]的信任度评估模型都将信任的主观性和不确定性等同于随机性,且没有明确区分直接信任和推荐信任,无法有效地消除恶意推荐带来的影响.对主观信任进行研究,远比对客观信任研究要复杂得多.主观信任模型主要从信任的定义出发,使用数学的方法来描述信任意向的获取和评价.
文献[4]考察了主观信任的模糊性,构造了一个基于模糊集合理论的主观信任管理模型,并给出了信任类型和信任的综合评价方法.但在权衡指标权重时仅仅由专家主观上给出一定值,并不能较好的反映各指标在实际中所占的比重.文献[5]将指标进行无量纲化处理,建立了一种基于模糊理论的主观信任综合评价模型.但在评估指标权重时,和文献[4]类似,采用专家主观意识上的赋权,带有很大的主观性.由于专家的经验、认识水平有较大的差异,仅仅赋简单的权重可能会使评估的结果与实际的结果有较大的差异.
为克服主观赋权的片面性,本文由综合分析法得到的指标权重,提出了一种基于模糊贴近度的主观信任模型.先分别通过主观分析法,如层次分析法[6]和客观分析法,如主成分分析法[7]得到各自的指标权重,然后通过一种综合权重模型得到评判指标的综合权重.最后由Fuzzy集与隶属函数相对应关系,模仿概率论中的正态分布函数,建立了一种基于贴近度的信任评估模型.
1 相关定义与运算
定义1[8]设给定论域U,所谓U上的一个模糊子集合A是指对任意的x∈U,都能确定一个数μA(x)∈[0,1],用这个数表示x属于A的程度.
映射μA:U→[0,1],x→μA(x)∈[0,1],称为A的隶属函数,μA(x)称为U中的元素对模糊子集合A的隶属度.
定义2[9]设X≠覫,T哿F(X),N:T×T→[0,1]且对于任意A,B,C∈T,满足条件:
(Ⅰ)若A≠覫,则N(A,A)=1;
(Ⅱ)若A∩B=覫,则N(B,A)=N(A,B)=0;
(Ⅲ)若C哿B哿A,则N(C,A)≤N(B,A).称N为在T上的贴近函数,N(B,A)称为在T上B对A的贴近度.
设X≠覫,T哿F(X)且T是X上的正规Fuzzy集的全体(即A∈T,当且仅当埚x∈X,使μA(x)=1),N:T×T→[0,1],对于任意的A,B∈T,令

任意一个Fuzzy集都与一个隶属函数对应,模仿概率论中的分布函数,在论域是实数集的情形下确定的一个Fuzzy集的隶属函数,称之为Fuzzy分布函数.
定义3 设a,σ 为实数,且σ>0,则

为Fuzzy分布函数,也即正态性分布.
2 综合确定指标的权重
2.1 层次分析法确定权重
设A={A1,A2,…,An}是全部指标集,aij表示指标Ai对指标Aj的相对重要性数值,则矩阵A=(aij)n×n为比较判断矩阵.其中aij=f(Ai,Aj)>0(aij的取值一般取正整数1-9及其倒数).将指标体系中的各个指标进行两两比较而得出的比较判断矩阵A:

根据比较判断矩阵A,求出矩阵的特征向量,所求的特征向量即为评判指标的权重.方根法是层次分析法中求特征向量的一种有效方法,保证了所得到的特征向量的正值性和唯一性.
方根法求比较判断矩阵A的特征向量:
(Ⅰ)计算A中每一行元素的乘积Ai

(Ⅱ)计算Ai的n次方根W軘i


则W=(ω1,ω2,…,ωn)即为所求特征向量.
由此,得到指标A={A1,A2,…,An}的权重向量为WH=W.
2.2 主成分分析法确定权重
设A={A1,A2,…,An}是全部指标集(原指标),它们的综合指标(新指标)为

则新指标向量B=(B1,B2,…,Bm)T为原指标A={A1,A2,…,An)T的线性组合,即

其中B1是A1,A2,…,An的一切线性组合中方差最大者,称为第一主成分;B2是与B1不相关的A1,A2,…,An的所有线性组合中方差最大者,称为第二主成分;……;Bm是与B1,B2,…,Bm-1都不相关的A1,A2,…,An的所有线性组合中方差最大者,称为第m主成分.
依据原指标Ai与Aj的相关系数矩阵R,求出特征方程

的m个特征值λi(i=1,2,…,m,λ1>λ2>…>λm)所对应的特征向量,如果第一主成分B1的贡献率

则对应的特征向量可以近似的看成是原始指标的权重向量.如果α1不够大,可以取前几个主成分的贡献率和对应特征向量值的乘积组合,经归一化处理后得到评判指标的权重向量为WM.
2.3 综合分析确定指标的权重
鉴于主观分析法,如层次分析法和客观分析法,如主成分分析法的片面性,本文设计一种综合分析法来获得指标的权重,该方法将这两类方法的结果有机的结合起来,得到的权重结果更能全面反映系统指标的本质.
设WH为AHP法得到的权重向量,WM为主成分分析法得到的权重向量,则综合权重模型为

t值取决于WH中各分量的差异程度.令

GH为AHP法中各分量的差异系数.

其中n为指标个数,ω1,ω2,…,ωn为WH中各分量从小到大的重新排序.
3 模糊综合评估
3.1 计算贴近度
假设在开放的网络环境中,要判断信息在网络中传输的可信度,就需要对网络中实体进行信任评估.现通过n个属性指标(指标)A1,A2,…,An来评估实体的信任等级.因为这些指标都具有Fuzzy性,故均用Fuzzy数表达.现有完全信任,一般信任,有点信任,不太信任和完全不信任5类信任等级,记为

用Pij=(i=1,2,…,n,j=1,2,…,5)表示第i类信任等级的第j个指标对应的Fuzzy集(数),由定义3则

现有信息传输要经过实体A,用Aj(j=1,2,…,5)表示该实体第j个指标对应的Fuzzy数,由定义3则

为此,对于贴近函数N,取定阈值λ0,由(1)式,则μpij(x)∧μQj(x)在使μpij(x)=μQj(x)时的x处达到最大值,从而得到贴近度为
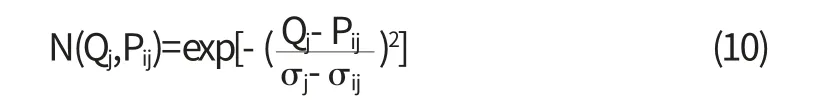
3.2 综合评估
网络的可信评估实际上是对网络中实体的指标进行综合评估.由(10)式得到的贴近度得:
(Ⅰ)若

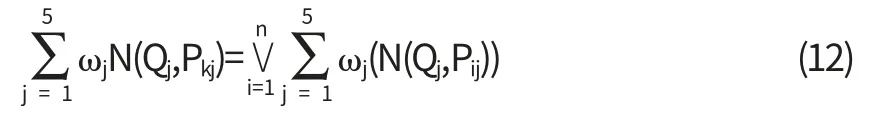
4 数值实例分析
4.1 信任综合评估的指标体系
在复杂的网络环境中,如果能对网络中主体的信任度进行合理的评估,就能够对通过该主体的数据信号的安全性和可靠性进行准确的判断.采用德尔菲法建立网络中主体综合评估指标体系如图1所示的层次结构.

图1 主体信任综合评估的指标体系
4.2 指标权重的确定
4.2.1 层次分析法
在对网络中的主体进行评估时,有专家对指标体系中的近期信誉、历史信誉、社会职务、社会声望和过程记录5个指标进行两两比较而得出的比较判断矩阵 .

由(2)(3)式可得,

4.2.2 主成分分析法
对于网络系统中主体信任的评估,将获得的近期信誉、历史信誉、社会职务、社会声望和过程记录5个指标的原始数据(原指标)按多元统计作标准化处理,由此得到的相关系数矩阵R.

由|R-λI|=0求出相关矩阵的特征值,以及各个主成分的贡献率与累计贡献率,得出的结果如表1所示.

表1 特征值及主成分贡献率
由表1中特征值所对应的特征向量矩阵C.

由表1可知,第一主成分的贡献率为

则对应的特征向量归一化后得到的权重向量
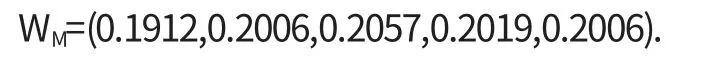
4.2.3 综合分析法确定指标的权重
由4.2.1节层次分析法得出的权重向量WH和4.2.2节主成分分析法得出的权重向量WM,依据(7)式,求层次分析法的差异系数

于是由(6)式,求得

于是由(5)式,综合权重为

4.3 信任的综合评估
令第i类信任等级的第j个指标对应的Fuzzy集Pij(i=1,2,…,5,j=1,2,…,5)及第j个指标对应的Fuzzy数Qj(j=1,2,…,5)为表2所示,以及Fuzzy集Pij(i=1,2,…,5,j=1,2,…,5)及第j个指标对应的Fuzzy数Qj(j=1,2,…,5)所对应的正态参数σij和σj,如表3所示.

表2 Fuzzy集Pij和Qj

表3 正态分布参数σij和σj
由表2和表3的结果,以及(8)(9)(10)式可得Pij与Qj的贴近度N(Qj,Pij)如表4所示.

表4 Pij与Qj的贴近度
设λ0=0.5,由(11)式和表4,则有于是判断该实体的信任度为第2类的“一般信任”.
5 结束语
鉴于主观信任的动态性和不确定性,人们利用不同的方法试图解决信任度量和评估问题,但都有不足之处.本文首先在考虑指标权重时采用了一种结合主客观的综合模型来获得指标的权重;其次在对主体进行信任评估时,引入模糊理论的隶属度,由Fuzzy集与隶属函数相对应关系,模仿概率论中的正态分布函数,提出了一种基于贴近度的主观信任模型.该模型避免了用精确的结果表示实体的信任度,只要判断出实体的贴近度大于某个阈值,就能评估实体的信任度.
〔1〕林闯,彭雪海.可信网络研究[J].计算机学报,2005,28(05):751-757.
〔2〕BETH T, BORCHERDING M, KLEIN B. Valuation of trust in open network [A]. Proceedings of the European Symposium on Research in Security (ESORICS)[C].Brighton:Springer-Verlag,1994.3-18.
〔3〕J·SANG A. A logic for uncertain probabilities [J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based System, 2001,9(3):279-311.
〔4〕唐文,陈钟.基于模糊集合理论的主观信任管理模型研究[J].软件学报,2003,14(8):1401-1408.
〔5〕黎梨苗,陈志刚,邓晓衡,等.基于模糊理论的主观信任综合评价模型研究[J].计算机应用研究,2010,35(11):39-42.
〔6〕王莲芳,许树柏.层次分析法引论[M].北京:中国人民大学出版社,1989.
〔7〕李春平,杨益民,葛莹玉.主成分分析法和层次分析法在对综合指标进行定量评价中的比较[J].南京财经大学学报,2005(6):54-57.
〔8〕张书钦,杨永田.对等网络中基于模糊集的信任和声望模型[J].哈尔滨工程大学学报,2005,26(6):763-766.
〔9〕赵汝怀,陈小君.模糊子集贴近度的普遍定义和模糊度[J].西安交通大学学报,1981,15(6):21-27.
