重要极限公式的新证法及推广

任建功，慕晓凯

（广东培正学院基础部，广东广州510830）

任建功，慕晓凯

（广东培正学院基础部，广东广州510830）

利用罗必达法则“1∞”极限的求法，巧妙地解决重要极限公式II的证明，并给出一些例子作以验证，得到此方法的简洁性.

罗必达法则；复合函数极限；重要极限公式II

微积分作为理工科类、财经管理类等各个专业都必修的核心课程之一，它对激发和培养大学生逻辑推理能力、思辨能力、创新能力的重要途径.在微积分内容里面重要极限公式证明时，在很多教科书中都是千篇一律地利用二项式定理来完成，但是很多学生很难掌握二项式展开，造成学生理解的困难.鉴于此况，给出了一种更简明证法.

利用二项式定理证明此极限时候，要用到二项式展开，单调有界准则，两面夹法则.在此种证明方法，主要利用指数与对数的转换，利用洛必达法则中“1∞”极限的求法，得出了此极限.通过比较，不难看出，利用此方法的证明过程比文献利用二项式定理展开的证明过程，要简单明了许多，更容易理解，并且需要的知识点都是平时接触过的.

对于重要极限公式的主要特征是：

1.它属于幂指函数求极限的问题，在自变量的变化过程中，底数趋向于1，幂指数趋向于无穷大，属于1∞型的未定式.

2.它的底数由两项所构成，第一项是1，第二项是趋向于无穷小量的变量.

3.底数中的第二项与幂指数的乘积的极限为常数.

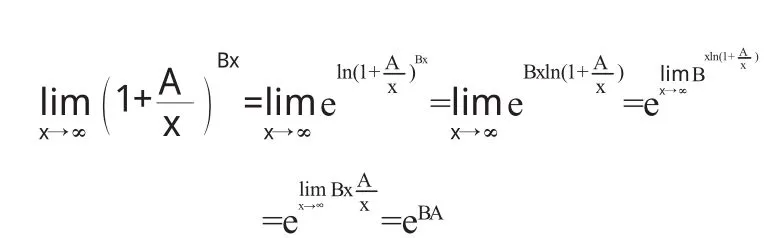
例1求极限

解

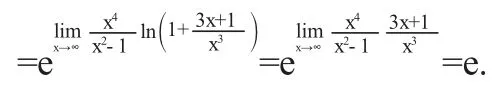
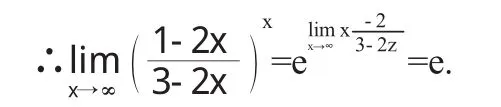
综上所述，我们在求幂指函数，尤其是重要极限公式II类型的函数极限的时候，不要再单一地利用重要极限公式II而去转化幂指数部分，可以通过洛必达法则“1∞”型未定式的方法，结合复合函数极限内容，从而简单地求得结果.

〔1〕徐名扬.两个重要极限公式的推广[J].江苏教育学院学报（自然科学版），2009（09）：51-53.

〔2〕迟彦惠.微积分（上册）广州：华南理工大学出版社，2009.

O171

A

1673-260X（2013）05-0012-01