盾构隧道内力分析方法的对比研究
2013-01-16姚超凡晏启祥
姚超凡,晏启祥,何 川,耿 萍
(西南交通大学交通隧道工程教育部重点实验室, 成都 610031)
1 概述
从盾构隧道诞生开始,围绕盾构隧道结构的分析方法就一直受到高度关注并不断有新的方法提出。目前,美国主要采用弹性地基圆环法,英国、法国、德国、澳大利亚、奥地利等国主要采用全周弹簧法和Muir Wood法,西班牙采用考虑地层结构相互作用的Buqera法,日本采用修正惯用法(均质圆环法)和梁-弹簧法[1]。国际隧道协会在盾构隧道衬砌设计指南中进一步将世界各国盾构隧道分析方法划分为3大类:基于材料强度的线性模型、经验模型以及基于弹性力学的连续介质模型。基于材料强度的线性模型又分为考虑和不考虑地层衬砌相互作用模型,基于弹性力学的连续介质模型又分为解析模型和数值分析模型,最终形成了细化的14种类盾构隧道力学分析模型[2]。
中国盾构隧道建设起步较晚[3],主要以借鉴国外经验为主,盾构隧道设计目前主要采用修正惯用法、弹性支撑法和梁-弹簧法[4]。梁-弹簧法以曲梁模拟管片,拉压弹簧、剪切弹簧和旋转弹簧模拟环向接头,在梁-弹簧法的基础上,使用径向压杆模拟地层径向反力,进一步形成了梁-弹簧-压杆法。这3种方法主要差别是地层弹性抗力和接头效应的处理上。鉴于修正惯用法、弹性支撑法和梁-弹簧-压杆法在国内盾构隧道中采用较多,为探明这3种方法的各自特点及其合理性,将对其分析原理及其适用性进行系统分析。
2 修正惯用法
修正惯用法是一种将隧道视为自由变形的圆环,采用荷载结构模型进行盾构隧道分析的方法。接头对结构刚度的影响通过采用小于1的刚度折减系数η来体现,不考虑接头的具体位置,见图1(a)。错缝拼装时,由于环与环间存在弯矩传递现象,设计中采用弯矩增大系数ξ来计及相邻两环对目标环引起的附加弯矩,这样,目标管片环管片的设计弯矩就取为(1+ξ)M,而接头设计弯矩则为(1-ξ)M。统计表明,对于错缝拼装,η一般取0.7~0.8,相应的附加弯矩增大系数ξ取0.2~0.5;而对于错缝拼装,η一般取0.6~0.7,相应的附加弯矩增大系数ξ一般取0[5]。由于自由变形圆环在对称荷载作用下可简化成如图1(b)所示的基本结构,通过其顶部弹性中心处相对角变和相对水平位移等于零的条件,可方便地计算出多余未知力和各截面的内力。
盾构隧道修正惯用法示意如图2所示,其荷载包括竖向均布荷载q、水平均布荷载e1、三角形分布荷载Δe、水平三角形抗力pk、结构重度ω及地基反力q+πω。通常假定水平三角形抗力分布在隧道水平轴±45°范围,其值与隧道侧向变形紧密相关。单一荷载引起的结构内力计算公式如表1[6]所示。将每一种荷载单独作用在隧道上,然后将每种荷载计算获得的截面内力进行叠加则可求出隧道的内力。

图1 自由变形圆环求解原理

图2 修正惯用法示意

表1 修正惯用法公式
注:θ为衬砌截面与Y轴正方向的夹角,以顺时针旋转为正;M(θ)为衬砌θ截面所受的弯矩,以内侧受拉为正;N(θ)为衬砌θ截面所受的轴力,以受压为正;R为圆形衬砌截面中性轴所在圆半径,可取隧道内外半径之和的一半。
3 弹性支承法
弹性支承法将隧道也视为自由变形圆环,不考虑管片接头对结构整体刚度的影响,按照“局部变形”理论,用具有与岩柱相同弹性特征的弹性支承模拟地层作用,并以铰接的方式作用在衬砌结构上[7-8],并假设隧道拱顶90°范围为脱离区,无弹性抗力且不需要施加弹性支撑。弹性支承一般设置径向弹簧和切向弹簧模拟。当弹簧出现拉力时,删去该弹簧并重新计算,直到所有弹簧受压为止,见图3。单个径向弹性弹簧的刚度可通过下式计算[9]
Kr=kr×A(1)
式中Kr——地层径向抗力系数,kN/m2;
A——单个独立岩柱与隧道的接触面积,m2;切向弹簧的刚度可近似取径向刚度的一半。
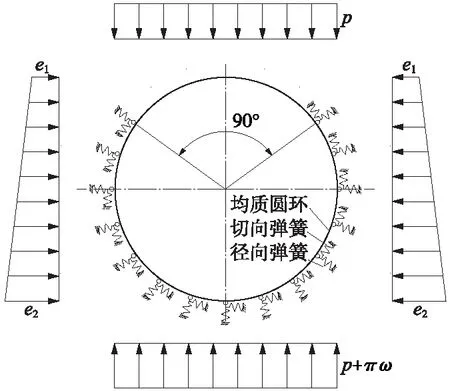
图3 弹性支承法示意
4 梁-弹簧-压杆法
梁-弹簧-压杆法采用梁单元模拟管片衬砌,用轴向、剪切和旋转弹簧模拟管片接头,用切向剪切弹簧模拟地层接触面切向力的传递,用压杆模拟地层接触面径向力的传递,见图4(a)。设置管片接头的剪切弹簧时,采用点位移耦合的方式,将两管片端头沿直径方向的相对位移提取到剪切弹簧的两端,以真实模拟管片接头的剪切力,见图4(b)。梁-弹簧-压杆法与弹性支承法的最大区别是前者考虑了管片接头效应,且事先并不假定弹性抗力的分布范围。梁-弹簧-压杆法涉及到的参数主要包括地层径向压杆和切向弹簧的刚度,管片接头的拉压弹簧、剪切弹簧和旋转弹簧的刚度。径向压杆和切向弹簧的刚度可按式(1)计算。
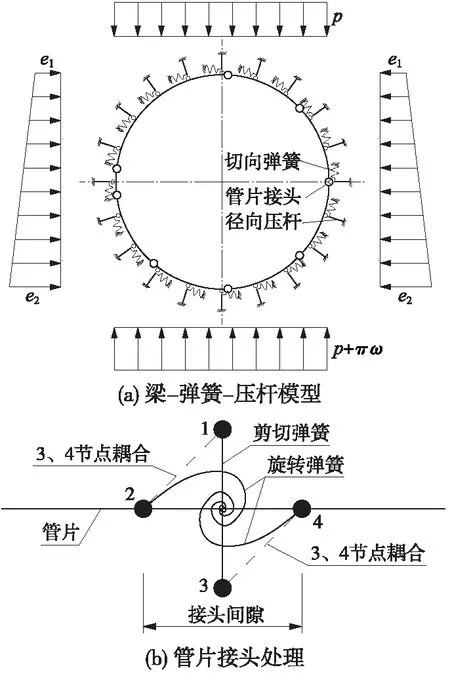
图4 梁-弹簧-压杆法示意
5 3种方法的对比
选取某外径为12.25 m、厚度为0.5 m的钢筋混凝土盾构隧道,在相同主动荷载下分别采用修正惯用法(以下简称方法一)、弹性支撑法(以下简称方法二)和梁-弹簧-压杆法(以下简称方法三)进行计算。该隧道采用“6+2+1”分块型式(图4(a)),通用楔形拼装。管片衬砌采用C50混凝土,其弹性模量为3.45×107kPa,密度为2 450 kg/m3,泊松比为0.2。隧道埋深28.45 m,水头为32.865 m,地层从上至下分别为粉土、淤泥质粉质黏土和粉质黏土,其厚度分别为17.9、11.63、14.88 m。采用太沙基理论进行围岩压力计算,计算获得的隧道竖向荷载p为380.55 kN/m,水平荷载e1为210.44 kN/m,e2(即e1与Δe之和)为348.20 kN/m,基底反力q+πω为417.50 kN/m。
地基径向抗力系数取7.0 MPa/m,由式(1)可以计算出地层接触面径向弹簧(或压杆)刚度为(5.5×105/n) kN/m,n为环向弹簧(或压杆)数量,切向弹簧刚度取径向刚度的一半。每环环向接缝采用25只M36纵向斜螺栓连接,每环衬砌纵缝内采用27只M36环向斜螺栓连接,螺栓机械强度等级8.8级。管片接头拉压弹簧刚度取3.98×109kN/m,剪切弹簧刚度取7.96×108kN/m,旋转弹簧刚度在隧道内侧受拉时取2×105kN·m/rad,外侧受拉时取1.2×105kN·m/rad[10-12]。地层接触面径向弹簧(或压杆)和切向弹簧数量都取1 600个。采用修正惯用法计算时,有效系数η取0.7。
3种方法所获得的管片衬砌弯矩(以内侧受拉为正,最大值和最小值分别指最大正值和最大负值)分布情况见图5,轴力(以受拉为正,最大值指最大受压值)分布情况见图6。
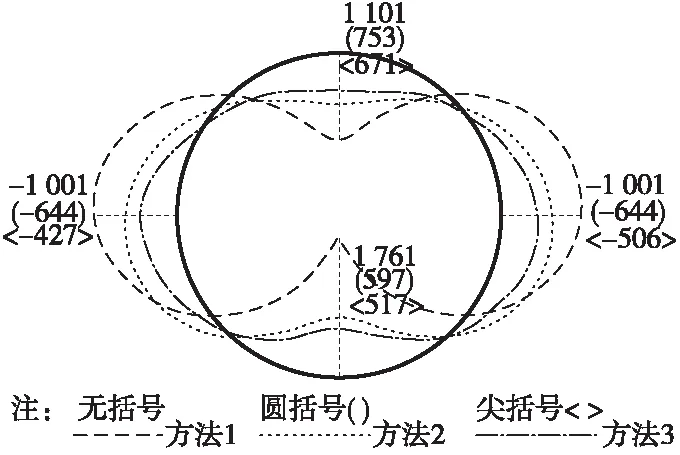
图5 管片衬砌弯矩(单位:kN·m)
从图5可见,最大弯矩值和最小弯矩值都出现在方法一所获得的弯矩分布图中,其值分别为1 761 kN·m和-1 001 kN·m,其次是方法二和方法三。方法三所获得的弯矩值最小,其原因可能是管片接头降低了结构整体抗弯刚度,从而导致相同外荷载下弯矩较小。方法一和方法二所获得的弯矩分布完全对称,而方法三弯矩分布不对称,这一差别主要是方法三中考虑了不对称分布的管片接头引起的。

图6 管片衬砌轴力(单位:kN)
从图6可见,3种方法所获得的轴力值都为负,说明管片衬砌各截面都处于受压的状态。拱底和拱顶处,采用方法三所获得轴力值最大,其次是方法二和方法一;左右拱腰处,采用方法一获得的轴力值最大,其次是方法二和方法三。轴力最大值出现在方法一,其值为-2 260 kN。总体上,采用3种方法所获得的衬砌各截面轴力值基本一致,说明考虑管片接头和地层切向作用对轴力大小的影响并不大。
方法二和方法三所获得的地层径向弹簧(或压杆)受力情况如图7所示(受拉为正),图中数字为单根径向弹簧(或压杆)的轴力值。从图可见,2种模型的地层径向弹簧(或压杆)分别在左右拱腰处88.6°(方法二左拱腰)、88.6°(方法二右拱腰)、83.5°(方法三左拱腰)、90.3°(方法三右拱腰)范围处于受压状态,拱底和拱底约90°范围出现了零值,这表明,方法一和方法二中预先假定的地层弹性抗力范围是基本合理的。
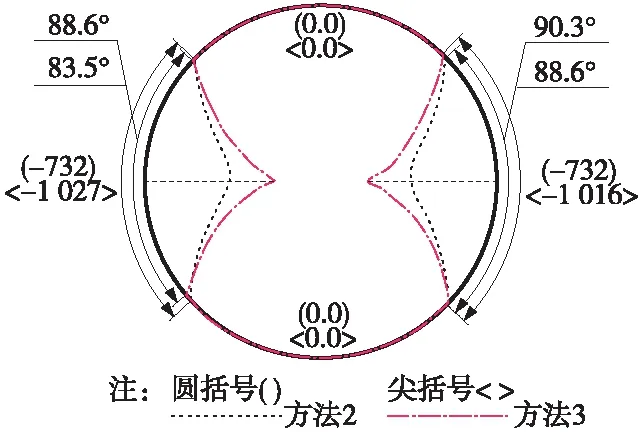
图7 地层径向弹簧(或压杆)受力(单位:N)
将方法二和方法三中水平左拱腰处的弹簧(或压杆)压力换算成管片衬砌的水平作用力,并将其与方法一中水平左拱腰处弹性抗力值进行对比,水平弹性抗力从大到小依次出现在方法三、方法二和方法一中。与方法二相比,方法三水平弹性抗力更大的原因可能是管片接头削弱了衬砌的整体刚度,导致相同荷载下结构变形较大,从而引起了较大的地层弹性抗力。主要分布在衬砌左右两侧的地层径向弹性抗力相当于减小了围岩压力,其通常将导致管片衬砌弯矩减小,轴力增大。由于方法三、方法二、方法一的水平弹性抗力值依次减小,其将直接导致弯矩最大值和最小值绝对值依次反向按照方法一、方法二和方法三减小,而拱顶和拱底处轴力绝对值依次按照方法三、方法二和方法一增大。
方法二和方法三所得地层结构接触面的切向弹簧受力如图8所示(受拉为正),图上标注的数字为单个切向弹簧的轴力值。从图可见,2种方法所得拱顶到右拱腰和拱底到左拱腰处的切向弹簧受拉,而拱顶到左拱腰和拱底到右拱腰处的切向弹簧受压。对管片衬砌而言,切向弹簧作用力方向在上半环指向拱顶方向,下半环指向拱底方向。在地层切向力的作用下,管片衬砌拱顶和拱底会出现压力,左右拱腰会出现拉力,其效果等同于增大了拱顶和拱底的轴向压力值,减小了左右拱腰的轴向压力值。这是拱顶和拱底处轴力绝对值从大到小依次出现在方法三、方法二和方法一中,左右拱腰处轴力绝对值从大到小依次出现在方法一、方法二和方法三中的另外一个重要原因。
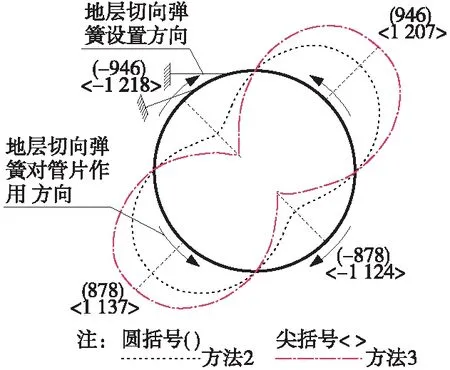
图8 地层切向弹簧受力(单位:N)
6 结语
对修正惯用法、弹性支承法和梁-弹簧-压杆法的计算原理进行了阐述,并通过具体实例进行了研究分析,研究表明如下结论。
(1)3种方法对接头的处理不同导致了衬砌结构的整体刚度差异。修正惯用法采用小于1的刚度折减系数η来体现管片接头对结构刚度的影响;弹性支承法忽略衬砌接头的影响;梁-弹簧-压杆法通过设置拉压弹簧、剪切弹簧和弯曲弹簧来模拟管片接头。是否考虑管片接头效应对结构的整体刚度影响较大,从而对衬砌弯矩影响较大,但对衬砌轴力值的影响非常有限。
(2)地层弹性抗力的大小与结构整体刚度有关,一般而言,结构整体刚度越小,地层弹性抗力越大。径向弹性抗力有助于削弱管片衬砌弯矩,增大管片衬砌轴力,且对拱顶拱底的轴力增大效果更明显;切向弹性抗力有助于增大拱顶和拱底轴力,减小左右拱腰处轴力。
(3)弹性支承法和梁-弹簧-压杆法获得的弹性抗力分布范围与修正惯用法的假定范围基本一致。且弹性支承法和梁-弹簧-压杆法获得的径向弹性抗力与修正惯用法假定的水平弹性抗力具有相似的效果,说明预先假定弹性抗力分布范围和大小的修正惯用法具有较好的适用性。
(4)3种方法所获得的管片衬砌弯矩值和轴力值分布形态基本一致,最大弯矩值都出现在拱顶或拱底。在外荷载一定的情况下,修正惯用法获得的弯矩值最大,弹性支承法次之,梁-弹簧-压杆法最小,而轴力值的大小变化不大。
(5)修正惯用法概念清晰,计算简便,且计算结果偏于安全,可作为盾构隧道内力计算的简要方法;弹性支承法没有考虑管片接头效应,适宜于编制成有限元计算程序,具有广泛的应用空间和比修正惯性法更高的精度;梁-弹簧-压杆法能模拟管片接头和充分考虑了地层结构相互作用,受力分析时精度更高,但较为复杂。因此,盾构隧道初步设计时可采用结果偏于安全且简便的修正惯用法,施工图设计时采用可编程且精度更高的弹性支承法,工程研究分析时采用能考虑接头效应的梁-弹簧-压杆法。
[1] 何川,张志强,肖明清.水下隧道[M].成都:西南交通大学出版社,2011.
[2] Working Group NO.2 of International Tunnelling Association, Guidelines for the Design of Shield Tunnel Lining[J]. Tunnelling and Underground Space Technology, 2000,15(3):303-331.
[3] 晏启祥,程曦,何川.深埋双圆盾构隧道衬砌荷载模式及其接头效应分析[J]. 铁道标准设计,2010(10):92-95.
[4] 李志业,曾艳华.地下结构设计原理与方法[M].成都:西南交通大学出版社,2003.
[5] 何川,张建刚,苏宗贤. 大断面水下盾构隧道结构力学特性[M].北京:科学出版社,2010.
[6] 刘铁雄,译.日本隧道标准规范(盾构篇)及解释[M].成都:西南交通大学出版社,1993.
[7] 张厚美,吕国梁.圆形隧道衬砌结构计算模型综述[J].世界隧道,2000(2):1-5.
[8] 曾东洋,何川. 盾构隧道衬结构内力计算方法的对比分析研究[J]. 地下空间与工程学报,2005,1(5):707-712.
[9] 村上博智,小泉淳.二次覆工された千鳥組セグメントリングの挙動について[J].土木学会論文集,1991(6):135-142.
[10] 陈俊生,莫海鸥.盾构隧道管片接头抗弯刚度的三维数值计算[J]. 铁道学报,2009,31(4):87-91.
[11] 曾东洋,何川.地铁盾构隧道管片接头抗弯刚度的数值计算[J].西南交通大学学报,2004,39(6):744-748.
[12] 张厚美,叶均良,过迟.盾构隧道管片接头抗弯刚度的经验公式[J].现代隧道技术,2002,39(2):12-16.
