地铁隧道列车运行诱发环境二次振动初探

2013-01-16罗伟,陈嵘,颜乐,王宇

铁道标准设计 2013年12期

罗伟,陈嵘,颜乐,王宇

(西南交通大学高速铁路线路工程教育部重点实验室, 成都 610031)

随着地铁的快速发展和居民对环境关注度的提高，地铁列车振动荷载作用对周围建筑物和环境的影响问题日益受到人们的重视，因此，很有必要对地铁列车运行引起的环境振动进行预测与评估[1]。

对地铁列车运行引起的环境振动进行预测与评估，是一个复杂的三维空间问题，针对这一问题，常用的方法主要有解析分析法、数值分析法、经验预测法和试验实测法[2-3]，目前，现有方法大都是基于现场测试，并进行频谱分析，以获得地铁沿线土体及沿线建筑物在列车荷载作用下的动力特性[4]。而就数值方法而言，国内流行的方法是采用忽略轨道结构影响的人工定数激励，进行土体及环境振动的研究[7]。为准确地模拟列车荷载的实际作用情况，避免因采用人工定数激励无法真实还原实际情况造成的偏差，将列车与轨道结构之间的动力作用机理列入了考虑。对列车-隧道-地基-自由场地-建筑物这一复杂的振动体系性，从系统各组成部分之间的耦合关系出发，通过建立列车-轨道-隧道子系统模型(以下统称振源模型)和隧道-土-建筑子系统模型(以下统称传播路径模型)2个子系统模型，从而建立起列车-隧道-地面体系的动力分析模型，研究了隧道周围土体及沿线建筑物的动力特性，初步探讨了地铁列车振动对环境的影响，以期为轨道交通的减振降噪研究提供参考。

1 工程概况

以深圳地铁某区间隧道线路为例进行分析，该区间线路采用了轨道减振措施——橡胶隔振垫浮置板轨道，轨道结构如图1所示。此区间线路采用6辆A车编组，设计速度为100 km/h。

图1 橡胶隔振垫浮置板轨道

2 振源模型分析

2.1 参数选取

A型车参数如表1所示。

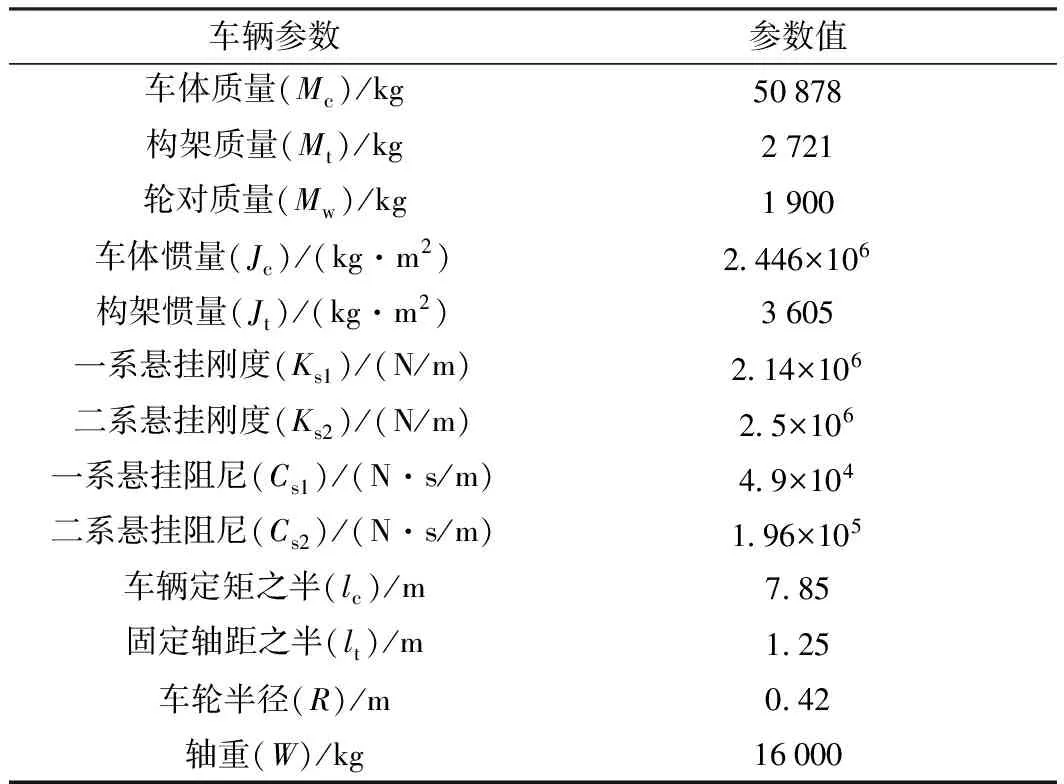
表1 地铁A型车参数

线路采用60 kg/m钢轨，轨道参数如表2所示。

输入轨道不平顺激励选用美国6级轨道谱，时域样本如图2所示。

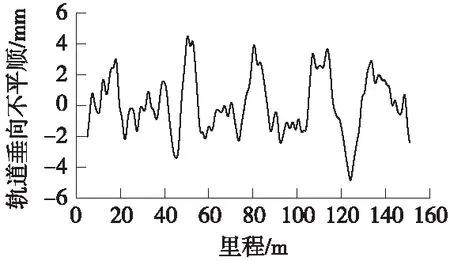
图2 轨道不平顺时程曲线

参数量值扣件轨道板道床板橡胶隔振垫钢弹簧垂向刚度/(N/m)250×107间距/mm630弹性模量/Pa360×1010宽度/mm2500厚度/m035密度/(kg/m3)2500泊松比020弹性模量/Pa325×1010宽度/mm3000厚度/m033密度/(kg/m3)2500泊松比020垂向刚度/(N/m3)0019垂向阻尼/(N(m/s))2×106垂向刚度/(N/m)76×106

2.2 计算模型

应用ANSYS有限元软件，建立了振源模型(列车-轨道-隧道动力耦合模型)如图3所示。

图3 振源模型

2.3 列车动荷载

通过此模型输入实际的列车、轨道、隧道承力结构参数，获得列车动荷载，在此处表现为连接道床板与隧道支撑结构的钢弹簧的弹簧力。列举作用于模型第一块轨道板边缘处某钢弹簧的列车动荷载如图4所示。

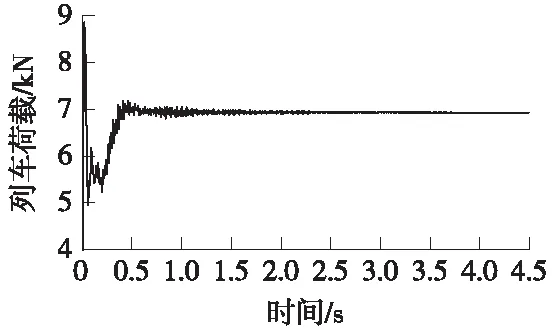
图4 作用于某钢弹簧上的列车动荷载

由图4可以看出，初始时刻，由于列车启动对轨道产生较大的冲击作用，弹簧力在这一时刻出现较大的波动。0.5 s之后，弹簧力稳定在7 kN附近，因轨道连续的不平顺的存在，列车对轨道的冲击作用使弹簧力上下浮动。随着车轮逐渐远离该弹簧所在位置，其冲击作用对该点的影响逐渐减弱。

3 传播路径模型分析

3.1 计算模型

应用ABAQUS数值分析软件，建立传播路径模型(隧道-土体-建筑系统的有限元与无限边界元耦合模型)如图5所示。考虑对称性，取半边土体进行计算，沿线路方向(纵向)取150 m，横向取100 m，深度方向(垂向)取35 m。土体上表面为自由表面，无限单元远端为自由边界，其余边界均为法向约束。

图5 传播路径模型

3.2 土体参数

针对深圳地铁某区间勘测资料、围岩自上而下的地质情况，将其综合归为8层材料性质的岩土进行分析。土体主要参数如表3所示。

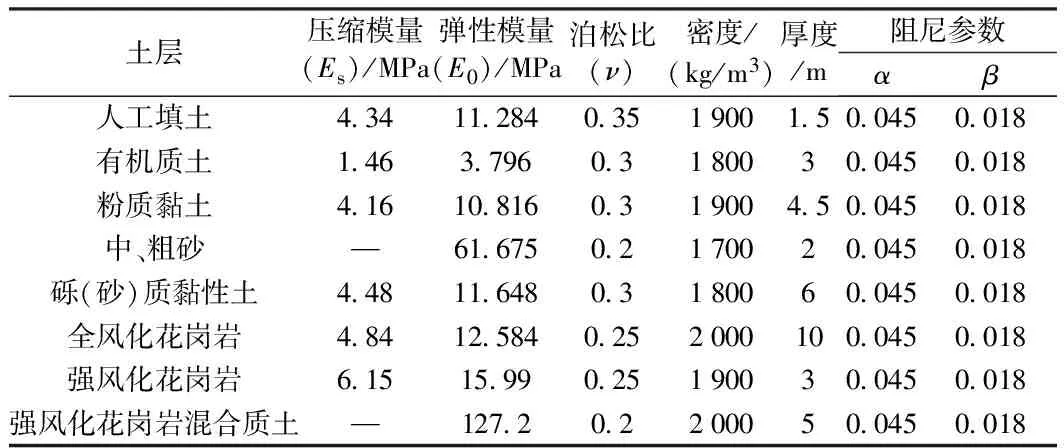
表3 土体主要参数

其他参数：衬砌和楼柱采用C40混凝土，弹性模量为3 250 MPa，泊松比为0.2，密度为2 400 kg/m3；楼板采用C25混凝土，弹性模量为2 800 MPa，泊松比为0.15，密度为2 400 kg/m3。

3.3 地面振动响应

图6、图7分别为列车通过时，距离隧道中心线10、15、30、45、60、80 m处地面最大竖向振动加速度和最大竖向振动加速度振级。

图6 地面最大竖向振动加速度

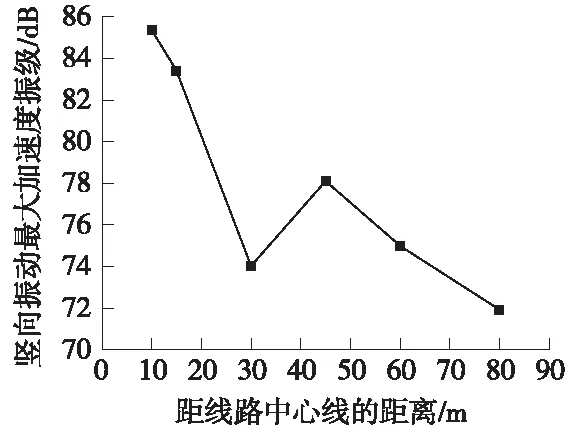
图7 地面最大竖向振动加速度振级

由图6、图7可以看出地面最大竖向振动加速度出现在距离隧道中心线10 m处，该点振动的加速度最大幅值为26 mm/s2左右，最大加速度振级为85.8 dB。竖向振动除了在45 m点出现反弹外，其他各点的振动时程曲线幅值基本上都是随着距离的增加而逐渐减小。

图8为列车通过时，距离隧道中心线10、15、30、45、60、80 m处地面竖向振动加速度幅频曲线。

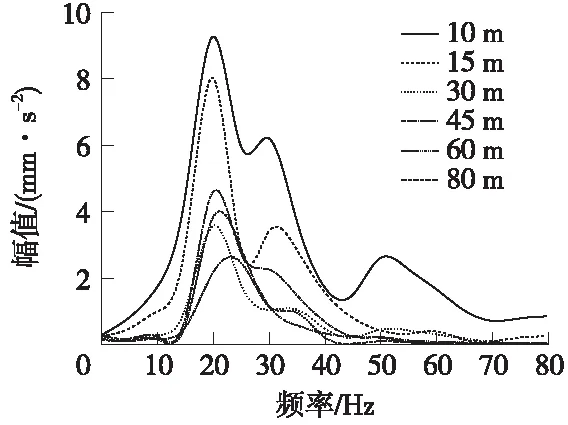
图8 地面竖向振动加速度幅频曲线

由图8可知，地铁列车运行引起的环境振动主要为低频振动，列车作用引起的地面最大竖向振动加速度发生在15～25 Hz，且随着距离的增加，较高频率内的加速度幅值衰减较快。

3.4 建筑振动响应

列车通过时，距离楼底净高分别为0、3.5、7、10.5 m的楼柱节点横向和纵向振动加速度如图9所示。

图9 楼柱节点水平向振动加速度

由图9可以看出，随着高度的增加，楼柱节点的横向振动加速度近似呈线性增加，表明在轮轨动力作用下，楼层横向处于一阶振动状态，属于低阶模态振动。楼柱横向振动加速度最大值为64.97 mm/s2，纵向振动加速度最大值为1.466 mm/s2，表明列车运行引起的建筑物水平方向上振动主要为横向振动。

列车通过时，各楼层的楼板最大竖向振动加速度如图10所示。

图10 楼板最大竖向振动加速度

由图10可以看出，随着高度的增加，楼板竖向振动加速度近似表现为一个恒定值，略有下降的趋势，楼板最大垂向振动加速度为9.95 mm/ s2。

楼柱节点距离楼底净高分别为0、3.5、7、10.5 m处横向振动加速度幅频曲线如图11所示。

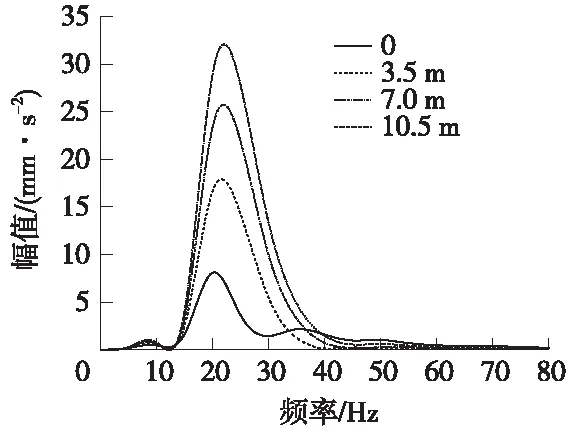
图11 楼柱节点横向振动加速度幅频曲线

由图11可以看出，列车振动作用引起的沿线建筑物楼柱节点横向振动加速度最大值发生在15～25 Hz，随着传播距离的增加，较高频率的振动成分快速衰减。

距离楼底净高分别为3.5、7、10.5 m处的楼板竖向振动加速度幅频曲线如图12所示。

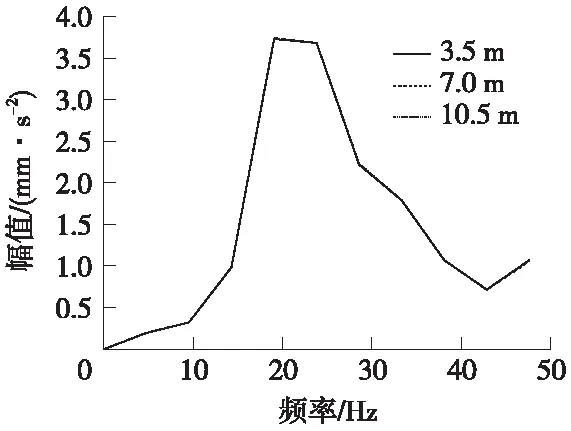
图12 楼板竖向振动加速度幅频曲线

由图11可知，列车作用引起的沿线建筑物各楼层竖向振动响应为恒定值，竖向振动加速度最大值发生在15～20 Hz，表明在轮轨动力作用引起的建筑物楼层的竖向振动为低频振动。

基础振动速度时程曲线如图13所示。

图13 建筑基础振动速度

由图13可以看出，基础纵向振动速度很小，表明列车运行几乎不引起基础纵向振动。基础竖向最大振动速度为5.56 mm/s，横向最大振动速度为4.02 mm/s。由于采用了土体为各项同性材料的假设，各土层各个方向剪切波的传播速度相同，所以竖向和横向振动时程曲线基本同相位。列车动力作用输入的能量在土体中传播，当振动波传递该点时，该点振动速度出现峰值，然后随着振动波向外继续向外传播，该点振动速度幅值衰减。