压杆失稳引起的振动分析
2020-05-29尚仁杰
尚仁杰
(中冶建筑研究总院有限公司 北京 100088)
引言
压杆广泛应用在各类结构中,压杆最关键的问题是整体稳定问题。欧拉最早提出了细长压杆失稳变形的弹性曲线问题,并用椭圆积分表示了细长压杆失稳变形挠曲线方程的精确解,目前,求解压杆稳定的方法有很多[1,2],但是,基本都是求解静力问题,或者是动态屈曲研究[3-5],很少去研究失稳的动力过程[6-8],而实际工程中失稳都伴随着突然的变形,引起强烈的振动。
对于轴向受压的细长弹性理想直杆,给杆件以微小侧向干扰使其稍微弯曲,则在去掉干扰后会出现两种不同情况:当轴向受压较小时,压杆最终恢复其原有直线形状;当轴向受压较大时,干扰会引起压杆侧向振动,并离开直线位置。可见,在轴向压力逐渐增大的过程中,压杆经历了两种不同性质的平衡状态:稳定直线平衡态和不稳定直线平衡态。理想轴心压杆,当轴向压力小于临界荷载Fcr时,压杆保持直线稳定平衡,见图1b的OA段;当压力超过Fcr时,杆件既可以在直线平衡段AC,也可以在弯曲平衡段AD,AC段是不稳定平衡状态,任何微小的扰动都会使其离开直线段AC而失去稳定,两种平衡的临界点A对应的荷载就是临界荷载Fcr。由于压杆在AC段积累了应变能,失稳时应变能的释放会引起压杆的侧向振动。失稳往往伴随着突跳[9],是瞬间的、快速的,本文就是研究从AC段不稳定直线平衡态失稳引起的振动以及失稳过程的时间。

图1 压杆及F-w示意Fig.1 Compressive bar and equilibrium path curve
1 压杆失稳过程微分方程
假设受压杆长度为2L,如图1所示,两端靠位移加载,加载到一定程度后控制两端的位置不动,分析压杆的稳定性,以及失稳的过程。
压杆失稳后产生侧向弯曲变形,变形后曲线方程可按式(1):
(1)
其中:w(t)为压杆中间点侧向位移值,是时间的函数。
压杆各点侧向位移速度为:
(2)
压杆变形曲线各点斜率为:
(3)
压杆变形曲线各点曲率为:
(4)
t时刻,压杆侧向运动的动能:
(5)
压杆失稳弯曲后曲线微段长度:
(6)
压杆曲线长度:
压杆长度变化:
(7)
失稳过程压杆界面弯矩为:
(8)
根据欧拉公式,压杆的临界荷载为:
(9)
设压杆压力达到临界值的α倍,即:
(10)
0时刻,压杆还未弯曲变形时,轴向压缩的应变能为:
(11)
t时刻,失稳侧向弯曲过程中弯曲应变能可根据式(8)积分得到:
(12)
t时刻,压缩应变能:
(13)
(14)
根据能量守恒:
EMt+EPt+EKt=EP0+Ek0
(15)
(16)
(17)
(18)
2 失稳过程振动分析
将方程(18)简化为:
(19)
2.1 无扰动,
①当α<1时,只有零解,w(t)=0。
②当α=1时,也只有零解,w(t)=0,原因是两端有轴向约束,要失稳,需要轴向压缩变形才可以。这与一般的临界荷载时失稳有些不同。

(α-1)aw2(t)-bw4(t)=0
(20)
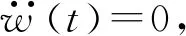
(21)
压杆达到新平衡位置时轴向变形新增:
压杆内力为:
(22)
重新达到临界轴力Fcr。
2.2 有微小扰动,为微小量
①当α<1时:

(23)
②当α=1时:

(24)


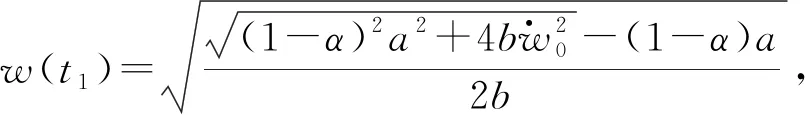
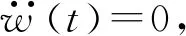
压杆失稳后找到一个新的平衡位置w(t2),达到w(t1)后开始返回。
从失稳开始到振动到最大位置的时间可通过数值积分[10]得到:
(25)
由此可以计算出失稳过程的时间。
3 算例
钢压杆,截面圆管,外径100mm,壁厚5mm,长度2L=10m,弹性模量E=2×1011N/m2,截面积A=1.492×10-3m2,截面惯性矩I=1.688×10-6m4,线密度m=11.71kg/m。
临界荷载:

α=1.25时,得到:

α=1.5时,得到:

α=2时,得到:



图2 压杆失稳过程相图Fig.2 Phase diagram of buckling of the bar
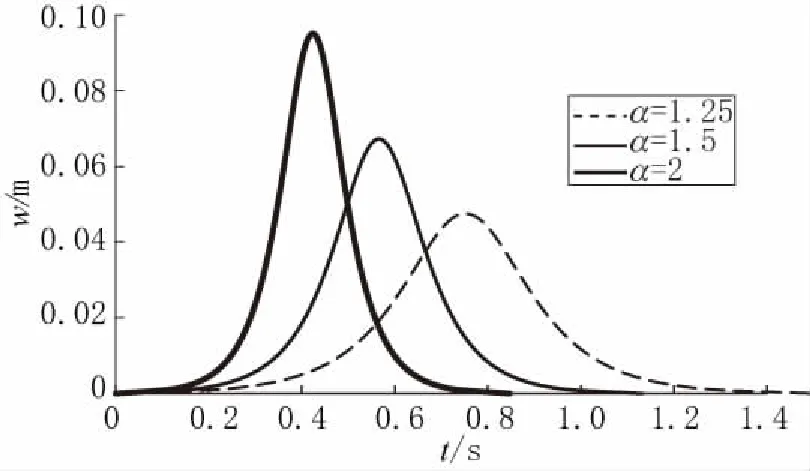
图3 压杆失稳过程时间-位移图Fig.3 Displacement-time curve of buckling of the bar
临界力Fcr=3.332×104N对应的应力为22.4MPa,10m长压杆压缩变形为1.12mm,加载采用位移控制加载,α=2对应的杆件压缩为2.24mm,如果加载在0.1s内压力达到α=2,压杆在α=1前失稳时由于来不及产生足够的侧向变形,压力会继续增大到α=2,积累应变能,随后产生侧向振动,侧向振动能量耗散后达到平衡位置,轴向力仍为Fcr;如果缓慢加载,压杆会在临界力前侧向失稳,来不及加载到α=2而产生大幅度弯曲,轴向力保持为Fcr。
4 结论
本文通过能量守恒推导了理想压杆失稳动力学过程的微分方程,通过微分方程分析和算例分析,可得到以下结论:
1.控制压杆两端位移的情况下,失稳过程微分方程可表达为:
2.当轴向压力不大于临界荷载时,振动为平衡位置的自由振动;
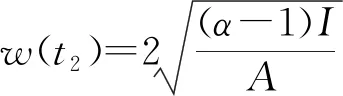
4.压杆失稳过程的位移-时间曲线见图3,轴向压力越大,失稳速度越快。
需要说明的是,本文是假设两端位移控制加载,当用荷载控制加载时,失稳过程会有所不同。
