不同电压下静电驱动膜片弹性变形分析

辛 超，李丽伟

(上海电力学院能源与机械工程学院，上海 200090)

微机电系统技术(MEMS)作为20世纪80年代发展起来的前沿性、多学科交叉的高科技技术，具有体积小、质量轻、能耗低、响应快、智能化，以及可大批量生产等特点［1］.静电驱动是MEMS中应用最广、最典型的动力驱动之一［2］，是一种使电能转换成机械能的方法，如静电微电机、静电微阀、静电谐振器等.静电力存在着固有非线性，与结构的弹性力、气膜阻尼力等耦合在一起后会形成多能域耦合的非线性特性［3］.非线性静电力作用下的微结构处于动态载荷的作用之下，构成了一个动态问题，仅仅在静力学上对其进行分析研究是不够的，无法揭示在外载荷作用下结构所表现出来的运动特性，因此对微结构给予动力学上的分析是必要的，它是设计和分析微结构的关键内容之一.

研究静电驱动微结构的动力学特性，把握静电力与结构运动特性的内在关系是提高静电驱动微器件研究水平的重要内容.

1 静电圆膜的结构模型

以传感器驱动膜片为例，进行弹性变形分析，继而基于Ansys软件进行驱动变形情况的模拟.传感器静电驱动结构模型如图1所示，驱动器上电极位于驱动圆膜上部，下电极位于腔体底部，腔体内部为流体，腔体一侧设置流体出入口.

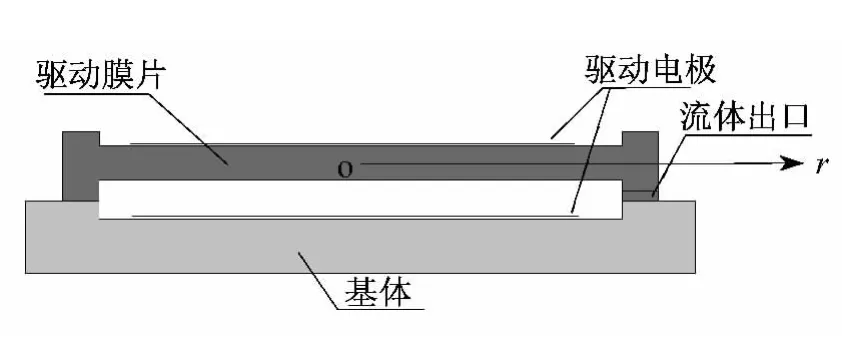
图1 传感器静电驱动结构模型

当传感器处于工作状态时，上下极板间加载周期性变化的电压，上下电极间存在电场，在静电力作用下，驱动膜产生弯曲和振动，使得腔体体积减少变化并迫使内部的气体流动，从而达到驱动的目的.

2 静电驱动薄膜的力学分析

2.1 驱动膜上所受的静电驱动力

驱动膜上所受的静电驱动力为:

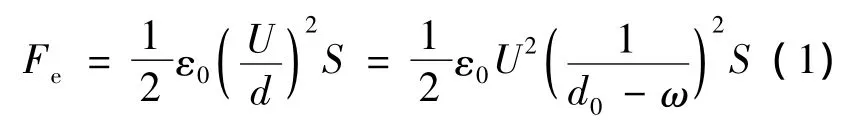
式中:U——上下电极之间的静电驱动电压;

d0——驱动膜与下电极初始距离;

S——驱动膜与下电极间的正对面积;

ω——板的挠度;

ε0——空气介电常数.

则作用于驱动膜片上的载荷为:

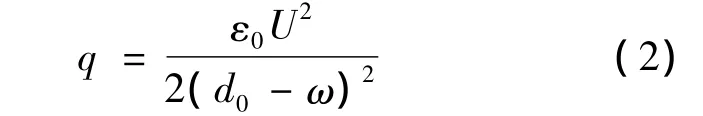
由于驱动膜片的振动为微幅振动，ω＜＜d0，故静电驱动的静电驱动力可简化为:

2.2 静电力作用膜片曲面方程

静电薄膜的尺寸如图2所示.根据弹性力学.以圆板中心为坐标原点，建立坐标系并建立圆形薄板的弹性曲面方程微分方程.其弹性曲面微分方程为:

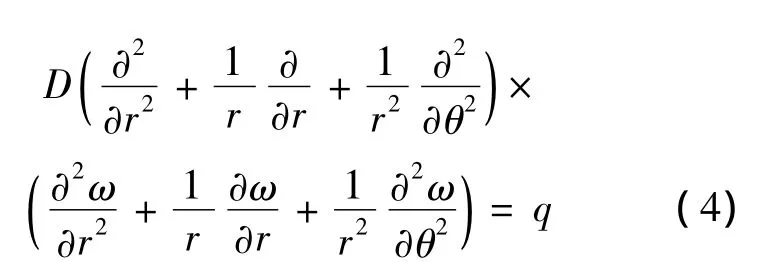
式中:r——测点到膜片中心的距离;

E——材料的弹性模量;

h——薄板的厚度;

λ——泊松比;

q——施加于薄板上的分布载荷，

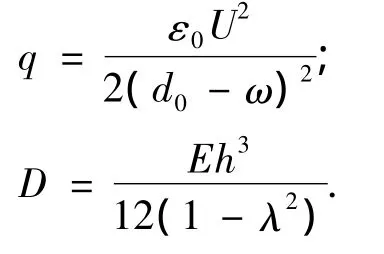
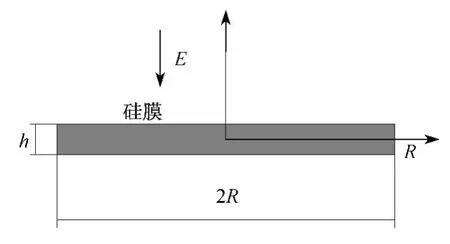
图2 驱动硅膜的几何尺寸

2.2.1 膜片受均布载荷

当忽略膜片变形引起的膜片上分布载荷的变化时，q=ε0U2/()，为一由加载电压决定的常数，膜片受到的载荷为均布载荷，这时可以求得:

2.2.2 膜片受非均布载荷

静电薄膜工作中，板间间隙并不是常量，而是随泵膜的变化发生非线性变化，从而造成静电载荷的非线性变化，可按泰勒级数展开，实现对非线性变化载荷的线性化，由式(2)可得:

在薄膜的小挠度范围，一般ω＜＜d0，忽略无穷小，取级数的前两项作近似处理，并令:

代入式(5)，根据固支边界条件，利用伽辽金加权残值法［3-5］进行求解，最终得到薄膜的挠曲面方程为:

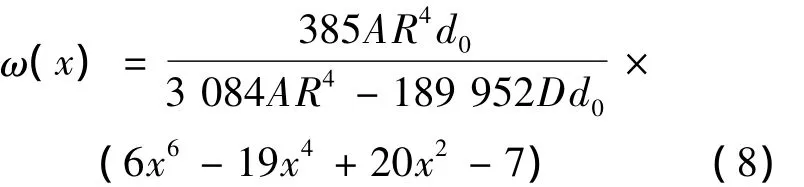
式中:x=r/R.

3 静电驱动薄膜的实例计算

薄膜的结构参数设置如下:厚度h=3 μm;半径R=1 000 μm;膜片与电极间的初始间距d0=10 μm;膜片的弹性模量 E=1.6 ×1011Pa;泊松比λ =0.22;空气介电常数 ε0=8.854 ×10-12F/m.

在周边固支条件下，通过Ansys建模仿真得到薄膜的前6阶模态，得出其一阶固有频率为22 901 Hz，其振型如图3所示.

图3 1/2膜片前6阶振动模态截面

由图3可以看出，静电薄膜在1阶振型条件下的容积变化率最大，运送效果最好;静电薄膜在2阶振型情况下不能很好作用，而更高阶的振型也难以达到效果.因此，在较低频率下利用薄膜的1阶振型来驱动流体流动是最佳选择.

在相同结构状况下计算静电薄膜振动临界电压，一般取当ω=1/3d0时，计算得出的临界电压约为40 V，在0～40 V时受均布载荷ω1和非均布载荷ω2两种振动的膜片的挠度变化计算结果如表1所示.

图4为不同电压下两种模型的挠度曲线图.由图4可以看出，在加载电压较小的情况下，两种模型挠度曲线基本重合，但随着加载电压的增大，非线性模型下膜片的挠度增加较快，以该算例为准，取加载电压为20 V时，计算得到两种算法的误差为2.76%.加载电压增加越多，薄膜的非线性变化越明显，误差越大.这是因为膜片挠度变化会影响膜片表面的载荷变化，膜片挠度越大，载荷在挠度较大的地方越集中，从而产生更大的挠度.由式(7)和式(8)可以看出，膜片的挠度与电压的平方成正比.

表1 不同电压下两种模型的挠度变化结果

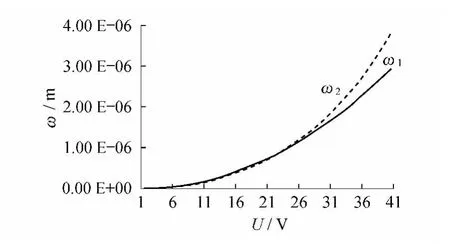
图4 不同电压下两种模型的挠度曲线

4 结语

本文以静电驱动膜片结构为例，对静电驱动模型进行了简化，得出了在膜片线性变化和非线性变化两种情况下，膜片的挠度与电压的平方成正比，由于挠度变化的非线性，进而得出两种方法的误差随着加载电压的增大而增大.以实际算例为例，介绍了两种方法在加载不同电压时的挠度变化，并仿真得出其固有频率为22 901 Hz，为静电微驱动控制提供了一定的理论依据.

［1］ 张文明.微机电系统(MEMS)动力学特性研究［D］.上海:上海交通大学，2008.

［2］ 南敬昌，刘元安，黎淑兰.RF MEMS器件驱动机制理论与分析［J］.微电子学，2006，36(4):416-417.

［3］ 王洪喜，陈光焱，赵剑.静电制动圆形微泵膜片的变形计算［J］.纳米技术与精密工程，2007，5(1):64-66.

［4］ 李俊，应济，周良兴.基于MEMS的静电微泵建模与仿真［J］.工程设计学报，2009，16(1):63-67.

［5］ 林谢昭，应济.基于模态分析的静电驱动圆薄板宏模型建立方法［J］.传感技术学报，2006，19(5):1 368-1 371.