散射长度周期变化下三势阱中玻色-爱因斯坦凝聚体的稳定性和隧穿特性研究

穆爱霞

(平凉医学高等专科学校 甘肃 平凉 744000)

1 引言

在玻色-爱因斯坦凝聚体实验以来，研究凝聚体在周期空间势阱中的行为是一个很重要的方向．双势阱相对来说是周期势阱中最简单的构形，在双势阱中描述内具体的最低价的近似是两模模型．通常，在线性情况下，通过调节周期场的调制参数可以控制体系的隧穿动力学[1～2]．Salmond等考虑在周期势阱中的两模近似下，沿x方向的周期性调制作用的效果就会使在双势阱的两个固定点附近振荡的晶格频率以及隧穿频率都变得与时间有关[3]．文献[4]讨论周期调制对非线性自囚禁的影响，把调制加在体系中两阱的最低能量差上，其强度为A，频率为ω，即y=Asinωt，用数值分析的方法研究轨道的整体性质．文献[5]主要考虑玻色-爱因斯坦凝聚(BEC)体的约瑟夫森结处于随时间变化势阱中的行为，在考虑热力学原子云与凝聚体的相互作用下，数值模拟了约瑟夫森结的动力学行为．Abdullaev和Kraenkel使用Melnikov方法讨论了随时间变化的隧穿系数K对系统Josephson效应的影响，给出了系统出现混沌的条件[6]．近来，运用Feshbach共振技术，s-波散射长度可也以调节成周期变化[6]．考虑到两体和三体相互作用都与s-波散射有关，三体系数也将呈周期变化．

在这里，我们讨论对称三势阱中散射长度周期变化时系统的特性，通过三模近似来处理含三体项的GP方程，以此为基础来分析定态解的稳定性．

2 散射长度周期变化下的三模近似

在考虑与时间有关的原子散射长度时，三势阱中弱耦合的BECs系统可以由方程(1)来支配．在这种情况下，g，ξ都是与时间有关的．通过Feshbach共振技术，我们可以使得原子散射长度成为时间的周期函数

A(τ)=A0+A1cosωτ

三势阱中有三体复合耗散及填充项存在时的GP方程被修改为如下形式

iћ∂tΨ(r,t)=

iξ′Ψ(r,t)4+iγΨ(r,t)

(1)

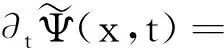
(2)

为了考查玻色-爱因斯坦在三势阱虑不周中的动力学特性，我们采用三模近似的方法来寻找方程(2)的解

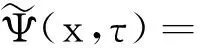
Ψ1(τ)Φ1+Ψ2(τ)Φ2+Ψ3(τ)Φ3

(3)

利用正交关系

(4)

其中i，j= 1,2,3，所以将方程(3)代入式(2)，并利用式(4)积分后得到下面三个非线性方程

i∂τΨ1=

(E1-U1Ψ12)Ψ1-K12Ψ2-

(5)

i∂τΨ2=

(E2-U2Ψ22)Ψ2-K12Ψ1-

(6)

i∂τΨ3=

(E3-U3Ψ32)Ψ3-K13Ψ1-

(7)

其中

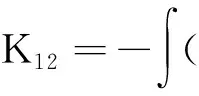
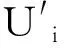
设

(8)

其中i=1,2,3，Ni(τ)是第i阱中的粒子数，θi(τ)是Ψi态的相，归一化的条件是N1+N2+N3=N,N是具有相同单位的三体凝聚体的粒子数．由以上条件，现将方程(8)代入方程(5)～(7)，其中Φ1=θ2-θ1,Φ2=θ3-θ1．为了了解三势阱中三体玻色-爱因斯坦凝聚体相互作用的新现象，我们仅考虑理想情况，即完全对称的情况．所以，令

U1=U2=U3=U

E1=E2=E3

阱1和阱2之间的粒子数差和阱2，3之间的相同，即

N1-N2=N3-N2

且忽略1，3阱之间的作用，考虑第一、二阱之间的隧穿率等于第二、三阱之间的隧穿率

Φ1=Φ2=Φ

K12=K23=K

则上面的方程变为

(9)

(10)

(11)

3 散射长度周期变化下的数值结果

3.1 三势阱中总粒子数随时间的变化

原子散射长度成为时间的周期函数

A(τ)=A0+A1cosωτ

图1 初始条件为N(0)=3,Z(0)=1,A1=0.12,Φ(0)=0,ω=2×192π，不同A0值所对应所的N随时间的变化

图1中，自上而下的曲线所对应的A0值依次为0.02，0.12，1，1.5．从图1可得知，对于同一A0值，N随时间增大，最终趋于一个定值．对于不同的A0值，随A0值的增大，N在趋于定值时越来越小．例如，A0=0.02时，N=129.6．而当A0=1.5时，N=1.9．我们发现，随A0值不断增大，即原子间相互作用增强，三体复合损失与a4成正比，这样，总粒子数N会不断减少．

3.2 散射长度周期变化下的隧穿特性

考虑与时间有关的原子散射长度A(τ)=A0+A1cosωτ时，三势阱中的弱耦合BECs可以用公式(5)～(7)来表示．

在图2(a)中，A0=2.5，原子布居数Z在零附近振荡，其幅值不断减小，最终到达一个负常数值，系统最终进入了自俘获态．图2(b)中，A0=1，原子布居数Z在零附近振荡，系统最终做周期运动．图2(c)中，取A0=0.12，原子布居数Z在零附近振荡，其幅值不断增大，最终Z到达一个负数值范围内，则系统依然进入了自俘获态．

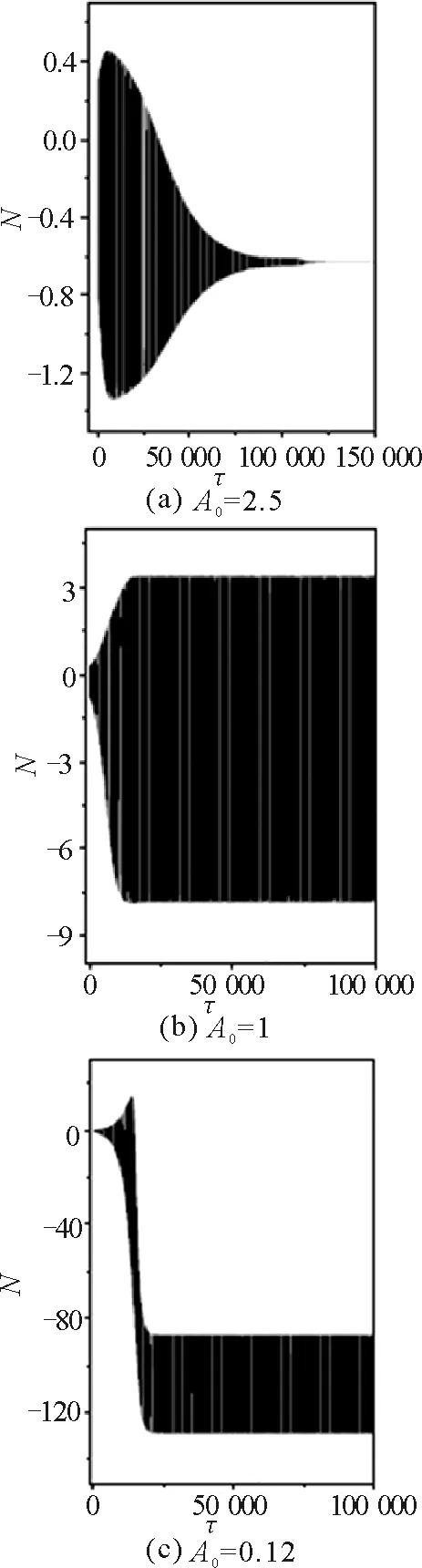
图2 初始条件N0=3,Z0=1,Φ(0)=0,A1=0.12,ω=2×192π时，不同A0值所对应的原子布居数Z随时间的变化．

本篇中我们研究了散射长度周期调制时对称三势阱中三体弱耦合BECs的隧穿特性．研究表明这个体系的隧穿动力学和自俘获可以被周期变化的散射长度有效地调节．关于这部分内容，更细致的研究今后将继续展开．

参考文献

1 J.M.Gomez Llorente and J.Plata.Tunneling control in a two-level system.Phys.Rev.A,1992,45:R6954

2 B.-Y.Ou,X.-G.Zhao,J.Liu,S.-G.Chen Phys.Lett.A,Nonlinear tunneling and chaos between two Bose-Einstein condensates trapped in time-dependent potential,291:17～21

3 G.L.Salmond,C.A.Holmes,and G.J.Milburn.A,Dynamics of a strongly driven two-component Bose-Einstein condensate.Phys.Rev.2002,65:033623

4 Guan-Fang Wang,Li-Bin Fu,Jie Liu.Periodic Modulation Effect on Self-Trapping of Two weakly coupled Bose-Einstein Condensates.Phys.Rev.A.,2006,73:013619

5 Yu-Fei Xiao,Deng-Long Wang,Feng-Jiao Wang,Xiao-Hong Yan.Acta Phys.Sin,Dynamic properties of an asymmetric josephson junction in Bose-Einstein condensates,2006,55:0547

6 F.Kh.Abdullaev,R.A.Kraenkel.,Macroscopic quantum tunneling and resonances in coupled Bose-Einstein condensates with oscillating atomic scattering length.Phys.Rev.A,2001,71:033603