载流圆线圈周围磁场分布

孟雨

(郑州大学物理工程学院 河南 郑州 450001)

圆电流的磁场分布是电磁学中一个重要而典型的问题，不少学者求解此问题时一般采用矢势方法，而即使采用最为基本的毕奥-萨伐尔定律求解时，求解的结果也是简化后的磁场在固定平面内的分布，而非整个三维空间内的分布．究其原因，在于积分的复杂性．即使求解磁场在平面内的分布，也涉及复杂的椭圆积分.因此对于磁场在三维空间任意处的分布，更为复杂．本文采用最为基本的毕奥-萨伐尔定律，通过一系列变量替换直接在直角系中给出了磁场分布的级数形式解．并通过数值模拟，形象给出了磁场在空间中的分布情况．

1 载流圆线圈磁感应强度

如图1所示，空间中一闭合圆线圈，其半径为R，圆线圈位于平面xOz内．

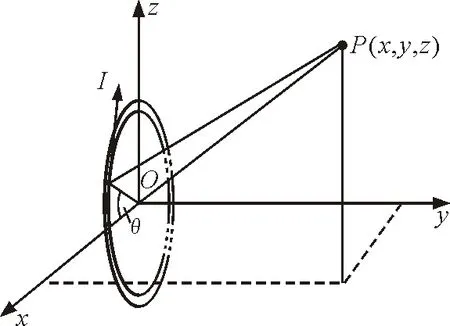
图1

不妨假设载流线圈中的电流I如图1所示的方向．现计算该载流回路在空间任一点P(x,y,z)处产生的磁感应强度．在载流回路上选取任一微元，其与x轴正方向夹角为θ，如上图所示．易知其位置坐标为(Rcosθ,0,Rsinθ)．则P点到该微元的距离r为

源点到场点的单位方向矢量为

则

(1)

其中

由Rθ=l，得dl=Rdθ，故

(2)

2 积分公式求解

分析式(2)中的积分不难发现，积分的困难就在于分母的复杂性．而分母可以表示为下面的形式

其中

(3)

因此本文就先从最基本的积分形式入手．令

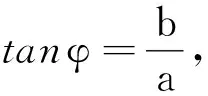
其中，通过分析不难发现，φ∈[-π,2π]，上式可改写为

(4)

其中

对I0的进一步求解过程如下.

设t=sinψ，则

(5)

(6)

以上两式相减，考虑到[3]

则

(7)

其中

由此得到等式

其中

故

(9)

对比式(2)中出现的积分，引入参量I1,I2并令

(10)

则由

得到结果

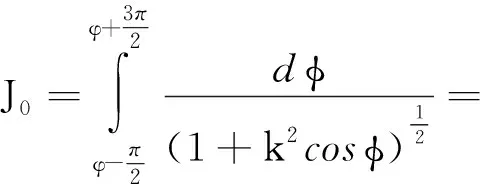
(11)

其中

将式(4)、(10)代入到式(2)中并整理，则得到以下结果

(12)

以上式(12)结果便是求解得到的载流圆线圈周围任意处空间磁感应强度分布，当然上式还不算是最终结果，因为式中所涉及的不完全椭圆积分的具体形式E(m,α,β)，J还没有确定，以下便是对其具体形式的求解．

3E(m,α,β)和J的计算

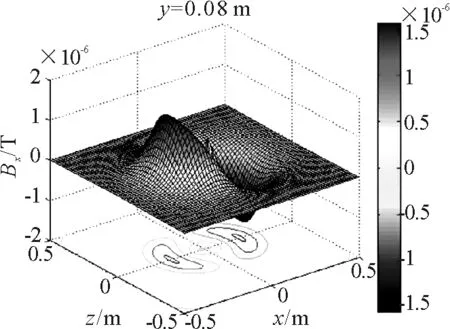
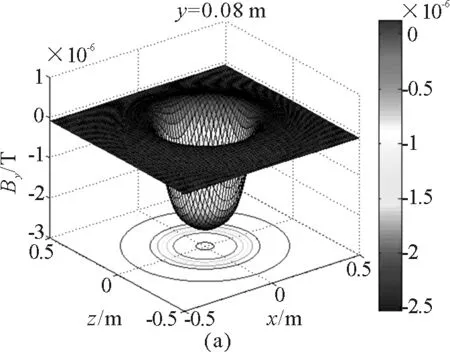
不难发现，当0

(13)

又由于

(14)

因此,原则上E(m,α,β)可求．由于

从而可以确定出

(15)

综上所述，式(12)已是严格意义上的精确解．至此，载流圆线圈周围任意处空间磁感应强度分布已由式(12)严格给出．

4 结果分析

虽然结果已由上文给出，但式(13)、(14)结果依然比较复杂，先对其进一步简化．考虑到

则由式(13)、(14)，并取幂级数前两项(第三项已趋于零)，得到

(16)

将相应α,β表达式代入式(8)、(16)，并取幂级首项，易得

M(α,β)=0

(17)

又由式(11)、(15)得

(18)

故最终

(19)

5 数值模拟

综合式(10)、(12)、(19)，用软件Matlab进行数值模拟，相关取值如下：μ0=12.566 370 614 4×10-7H·m-1;I=1 A;R=0.2 m.

首先对式(8)中的Bx进行数值模拟，由于目标函数Bx是关于空间变量x，y，z的三元函数，实际模拟时本文采用降维方法：由于圆线圈周围磁场关于y轴对称分布，故固定空间变量y，对目标函数进行三维模拟．当y取0.08 m时，磁场Bx分布如图2所示.

图2

同样道理，当y取0.08 m时，磁场By，Bz分布如图3所示.

图3

6 结语

对载流圆线圈周围磁场分布的求解一直都是一个经典问题，一方面在于圆形线圈的简单性，更重要的在于其方法的推广性和适用性很强．本文采用最为简单的方法，精确求解了载流圆线圈周围磁场分布．通过定性分析易知，By方向磁场关于坐标轴对称．由模拟结果可以明显看出，Bx，Bz分布具有相似性，且分布结果对称分布．由于数值模拟中计算E(m,α,β)时只取了幂级首项，因此结果会有稍许误差．在误差可允许的范围内本文的计算结果还是较为可信的．

参考文献

1 赵凯华,陈熙谋.电磁学(第三版).北京：高等教育出版社,2012.245

2 刘耀康.导出圆电流的磁感应强度的简便方法.大学物理,2007,26(7)

3 王竹溪，郭敬仁.特殊函数概论.北京：北京大学出版社,2000.549

4 张之翔.电磁学中几个简单问题里的椭圆积分.大学物理,2002,21(4)