几何光学与波动光学的“无缝”对接——透镜等光程性的教学研究

王勇强 吴明和 邬劭轶 黄卫英

(电子科技大学物理电子学院 四川 成都 610054)

张宗明

(绵阳中学 四川 绵阳 621000)

姚玲玲

(重庆市高治中学 重庆 404614)

1 引言

中学使用新课标后，中学物理课本中没有讲述薄透镜物像公式的高斯形式[1]，造成了学生较难理解不同方向的平行光与会聚在焦平面上焦点之间的对应关系，从而不能确定像点位置.而在大学物理教材中通常只对薄凸透镜的等光程性进行了定性说明，少有定量分析[2].为了将中学讲授的凸透镜成像实验规律与大学物理中的等光程概念有机结合起来，笔者对薄透镜物像公式的高斯形式进行了简单推导，证明了平行光斜入射情形下薄透镜的等光程性.

2 薄透镜物像公式高斯形式的简单推导

我们以凸透镜成像为例来说明物距u、像距v和焦距f之间的关系.如图1，设物高为h，像高为h′，由三角形AOB和三角形A′OB′相似，得到

(1)

又由三角形OO′F和三角形FA′B′相似，得到

(2)

式(1)、(2)联立，得到

(3)

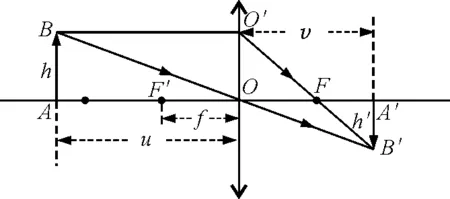
图1 薄凸透镜成像示意图

利用凸透镜成像的高斯公式(3)讨论不同物距下的像的大小，这样可以让学生回忆他们初中学过凸透镜成像的实验规律.

根据费马原理，多光线光程应该取极值或者恒定值，但是连续分布的实际光线光程取极大值和极小值是不可能的，所以光程必须相等[3].下面利用几何光学中的成像公式证明非轴线的物点和像点的多条光线中的两条光线等光程.

3 平行光斜入射情形下薄透镜的等光程性

如果物距为无穷远，但光线和主光轴不平行时，如图2，光线会聚于焦平面某一点，研究此种情形下的等光程问题.

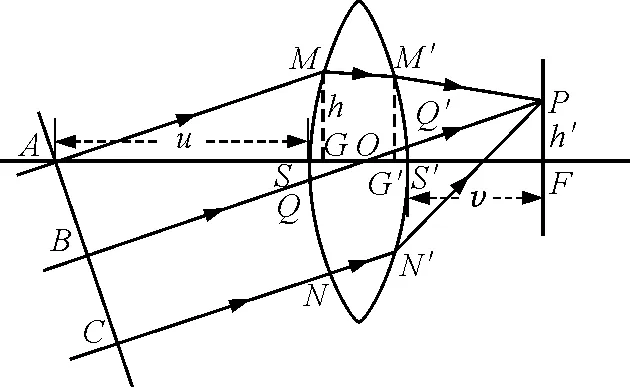
图2 平行光斜入射情形下薄透镜的等光程性示意图

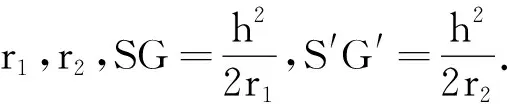
(4)

AMM′P的光程为

(5)

通过光心的光线BQOQ′光程为

(6)

其中AM光线和主光轴的夹角θ之余弦

(7)

式(5)～(7)都用到了牛顿二项式展开进行简化.

AMM′P和BQOQ′的光程差为

由公式(3),在u=∞，得到v=f，即与主光轴成夹角的来自无穷远的光线汇聚于焦平面的P点[4].从波动的观点看，A，B，C三点同位相，由于薄凸透镜不附加光程差，过A，B的平行光线通过透镜到P点光程相等，P点所有光线同相叠加，成明亮的像点.

4 结论

利用三角形相似，得到了凸透镜的几何成像公式；利用光程概念，证明了透镜主轴外物点和像点的等光程性，说明薄凸透镜不产生附加光程差；在中学教学中的成像实验规律和成像公式以及大学物理教学中的等光程概念之间建立了有机联系，实现了大学波动光学和中学几何光学的“无缝”对接.

参考文献

1 陈熙谋,吴祖仁.普通高中课程标准试验教科书:物理(选修加必修).北京：教育科学出版社,2012.3～4

2 郝玉英.薄透镜的等光程性证明.山西矿业学院学报，1996，14(4)：362～367

3 赵凯华.新概念物理教程:光学.北京:高等教育出版社,2011.38～48

4 姚启钧.光学教程.北京:高等教育出版社,1980.194