一道好题的魅力——有效习题课教学初探

李兰芳 万军

(江西省赣州第三中学 江西 赣州 341000)

在一次关于“力的动态平衡问题的解决方法”的习题复习课中，以一道蕴含多种思维方法的相关例题为主线进行教学．学生上课主动性得到充分的发挥，打破常规习题课中沉默的气氛．上课效率得到很大的提高．

题目：如图1所示装置，两根细绳拉住一球，保持两细绳间的夹角不变，若把整个装置以O点为轴顺时针缓慢转过90°，则在转动过程中，AC绳的拉力TAC大小变化情况是______，CB绳的拉力TBC的大小变化情况是______.

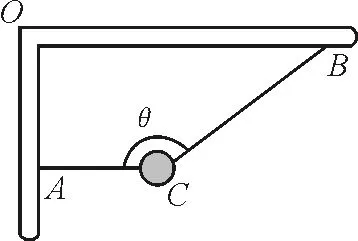
图1

课堂情况：课堂中采用学生分组讨论方式，并展示不同解法．因题目中有已知AC绳和CB绳夹角不变及重力恒定的特点，在展示的方法中，有比较多的同学画好受力图后，将力沿竖直和水平进行正交分解，建立平衡方程求解(如解法一)；也有少部分同学根据以上特点，应用正弦定理建立关系求解(如解法二)；另外，有极少数的同学应用了图解法(如解法三)．

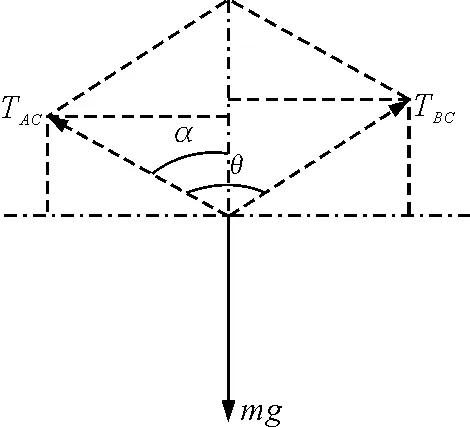
图2

解法一：设AC与竖直方向夹角为α(0≤α≤90°)，受力如图2所示，则任意时刻有

TACsinα=TBCsin(θ-α)

TACcosα+TBCcos(θ-α)=mg

利用三角函数和差化积化简得

当组合整体顺时针转动时α从90°逐渐变为零，这个过程中：TAC先变大后变小，TBC逐渐变小．

说明：正交分解法是解决力学问题最常用的方法，这也是绝大多数同学能想到的．

解法二：小球受力如图3所示.

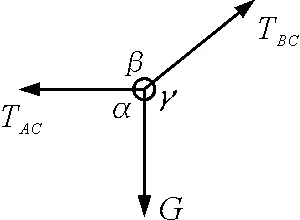
图3

根据题意并套用正弦定理

可知，G和β恒定，上式中三个比例式的值都恒定.角α从90°的基础上开始增大，角γ从大于90°开始减小到最后小于90°，所以TBC不断减小，TAC先变大后减小．

说明：如果是物体受到3个力处于平衡状态且题中明确给出几个力夹角的情况下，应用正弦定理就显得比较简单．这也是解析法处理力的动态平衡问题的情况之一．

解法三：小球受力如图4所示，因装置转动过程中两细线拉力方向夹角不变．即图中∠CAG′保持不变．则拉力交点应在同一圆周上．又因初位置细线CA水平，则圆心必在连线AG′的中点处．由图可看出拉力TAC先增大后减小；拉力TBC从最大值一直减小．

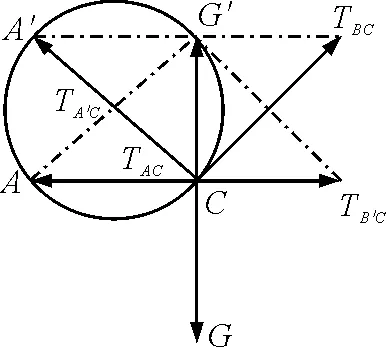
图4

说明：这一解法巧妙地应用圆的特点结合题意通过作图的方式求解出结果．此方法是图解法处理力的动态平衡问题的一种情况，适合于物体受3个力中有一个力恒定，其余两个方向间夹角恒定的情景．

通过以上同一题目中3种方法的展示，引导学生进一步思考在力的动态平衡问题中还会涉及的方法应用，并进行总结归纳．短时间的讨论后，绝大多数同学能很快地总结并补充完善．即处理力的动态平衡问题方法分为解析法和图解法两类．其中解析法中除以上特点会用的两种情况外，还有应用相似三角形建立关系求解，它主要应用于3力平衡中知道三角形的边长时情景(如例1)；而图解法中除以上情况外，还有常见情况“物体受3个力中有一个力是恒力，有一个力方向恒定”(如例2)．

【例1】如图5(a)所示，绳与杆均为轻质，承受弹力的最大值一定，O端用铰链固定，滑轮A在O点正上方(滑轮大小及摩擦均可忽略)，P端吊一重物．现施加拉力F将P缓慢上拉(均未断)，在OP杆达到竖直前

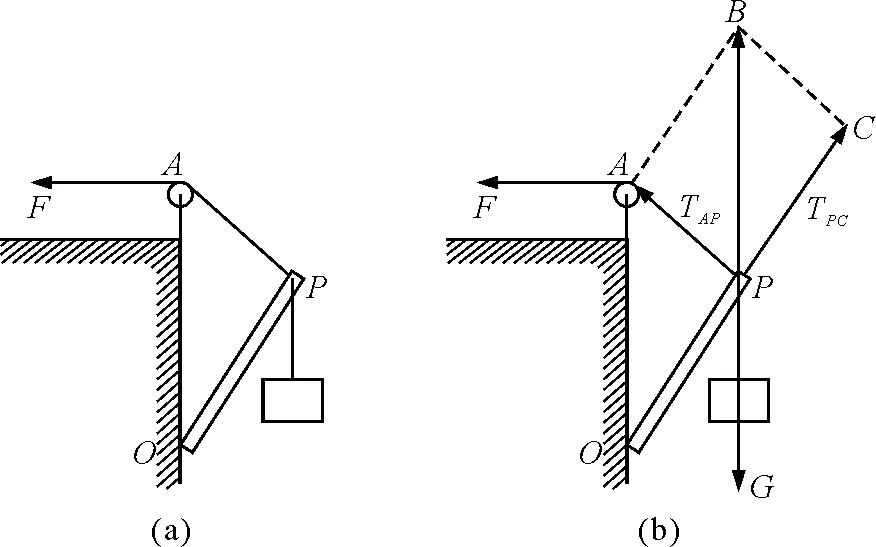
图5

A.绳子越来越容易断

B.绳子越来越不容易断

C.OP杆越来越容易断

D.OP杆越来越不容易断

分析：P点受到重物的拉力、沿杆的支持力、绳的拉力这3个力的作用，如图5(b)所示，当P点缓慢向上运动的过程中属于一个动态平衡态的过程，这3个力构成的闭合三角形一定与几何三角形OPA相似，因此对应边成比例．

解：P点受到向下的拉力大小等于物体的重力G，轻杆的弹力沿杆的方向用TPC表示，绳子的拉力用TPA表示，这3个力构成的闭合三角形如PCB所示，与长度三角形OPA相似．因此有

因为重力大小不变化，OA的长度不变，所以根据上面的比例式可知TPC的大小不变化，P点缓慢上拉的过程中PA的长度变短，所以绳上的拉力TPA变小，所以选项B正确．

【例2】如图6(a)所示，细线一端固定，另一端吊一重物P，重物P在被一水平向右的力作用下缓慢拉起．在此过程中，细线的拉力变化情况是

A．逐渐增大

B．逐渐减小

C．先减小后增大

D．先增大后减小

解：重物受力如图6(b)，重力不变，则平行四边形的对角线不变；拉力F方向不变，则平行四边形一组水平对边位置不变．故由图可以看出细线的拉力逐渐增大，选项A正确．

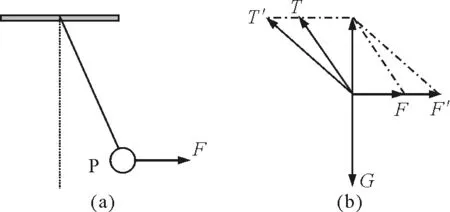
图6

综上所述，本节习题课中应用一个例题多方面分析、理解后只需要在细节上进行补充、完善就能将“力的动态平衡问题”中所涉及的方法和情景进行全面复习与巩固，以少量的题目达到全面的知识巩固，可见，优选一道好题，是我们上好一节习题课的重要一环．