Excel最小二乘法在磁阻效应实验中的应用*

唐春红 唐曙光 刘扬正

(南京工程学院基础部 江苏 南京 210067)

1 引言

磁阻器件由于灵敏度高、抗干扰能力强等优点在工业、交通、仪器仪表、医疗器械、探矿等领域应用十分广泛，其中最典型的锑化铟传感器是一种价格低廉、灵敏度高的磁电阻，因此，磁阻效应是普通物理实验课中的重要内容之一.本实验利用砷化镓霍尔传感器测量磁化强度，研究锑化铟传感器在不同的磁感应强度下的电阻大小.数据处理是该实验的重要组成部分和关键环节，也是评价实验结果的一个重要指标，该实验采用的数据处理方法有列表法、作图法、逐差法.特别是图解法处理虽然简单、直观，但它是一种粗略的数据处理方法.在图纸上用目测的方法拟合直线，具有一定的主观任意性，容易造成人为误差[1].更为科学的方法是最小二乘法曲线拟合，但由于该方法计算较复杂，在基础物理实验的数据处理中常常不被采用[2].

与Matlab、MathCAD图像处理、飞飞函数图像及Mathematical相比，Microsoft Office Excel(Excel)是大学一年级学生比较熟悉的数据处理工具，其拥有强大的计算、分析、传输和共享功能，可以帮助用户将繁杂的数据转化为信息.若是借助Excel强大的数值计算和高质量的绘图功能，将克服最小二乘法计算量大的缺点，使复杂繁琐的数据处理过程简单化、直观化，且能较准确地标记出实验数据点和绘制出拟合曲线.

2 最小二乘法原理及曲线拟合[3,4]

最小二乘法(又称最小平方法)是一种数学优化技术.它通过最小化误差的平方和寻找数据的最佳函数匹配.利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小.

2.1 线性参数的最小二乘法

求解得

2.2 非线性参数的最小二乘法

在一般情况下，函数yi=fi(x1,x2,…,xt)(i=1,2,…,n)为非线性函数，测量的误差方程

(1)

是非线性方程，直接由它建立正规方程并求解是困难的，一般采用线性化的方法，将非线性函数化为线性函数，再按线性参数的情况进行处理.为此，取x10,x20,…，xt0为待估计量x1,x2,…，xt的近似值，而估计量xr则可以表示为

(2)

式中δ1,δ2,…,δt为估计量与使取近似值的偏差.现将函数在x10,x20,…,xt0处展开，则有

fi(x1,x2,…，xt)=fi(x10,x20,…,xt0)+

令

则误差方程(1)化成线性方程组

(3)

于是，就可以按线性参数的情形列出正规方程并求解出δ，进而求得相应的估计量

xr(r=1,2,…,t)

3 用Excel处理磁阻效应实验数据

表1为我们在磁阻实验中记录原始数据及相关计算[5].

表1 磁感应强度和磁电阻大小的对应关系表 磁电阻电流I=1.00 mA

B/mT150.0200.0250.0300.0350.0400.0450.0500.0ΔRR(0)0.3970.4940.5800.6590.7420.8290.9191.008

选择数据→图表向导→XY散点图→点击图上数据点→点右键→添加趋势线→选多项式→阶数取值大于5后图形拟合的很好(图中阶数取为6)→取选项→显示公式及显示R平方值，结果如图1.

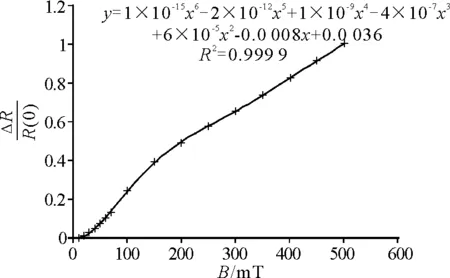
图1 锑化铟传感器不同磁感应强度下电阻大小的拟合曲线

由图1中可以看出相关系数R2代表拟合曲线的确定系数，用来检验拟合方程是否符合变量间的规律及拟合曲线的精度如何.R2值越接近1，说明实测数据点越靠近拟合曲线，趋势线越可靠.由图1可见R2值为0.999 9，说明拟合曲线几乎通过全部的实验点，则锑化铟传感器磁感应强度与电阻大小关系的曲线方程为

4×10-7B3+6×10-5B2-8×10-4B+3.6×10-3

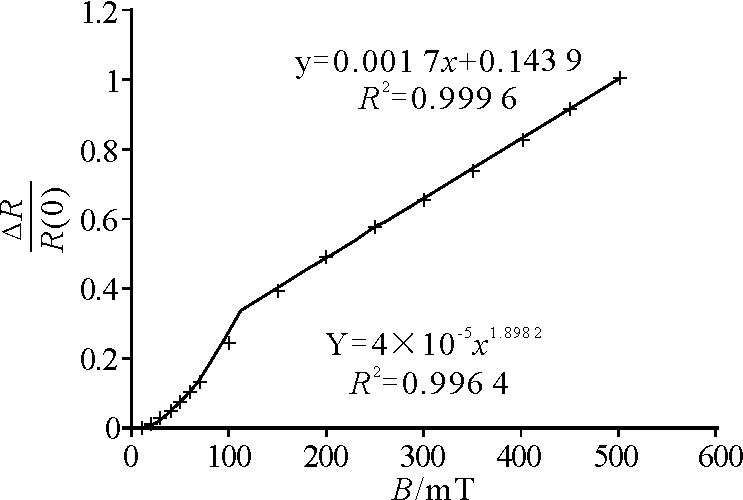
图2 锑化铟传感器B-关系曲线拟合的曲线方程

在[150.0,500.0]区域，n=1，k=0.001 7，曲线方程为

4 结论

在磁阻效应实验中,大学一年级的学生就可以利用自己熟悉的Excel，借助其强大的科学计算及绘图功能，能较准确地标记出实验数据点和绘制出拟合曲线.随着计算机运算能力的飞速发展，特别是Excel还可以进行Whst-If分析，以及执行更多更专业的分析，因此，如学生亲自参与编程操作，将计算机应用与物理实验结合起来，更能有效提高学生的计算机实际操作能力，使两学科的知识相互交叉，拓宽了学生的视野，激发了学生学习的兴趣，尤为重要的是通过Excel软件的使用可以有效地提高教学效率，为课程教学方法和手段的改革探索了新的思路.

参考文献

1 王礼祥, 蔡书, 刘一.Excel图表功能在数学、物理中应用的研究. 西南民族大学学报·自然科学，2012(1):150

2 韩敬，钟方川，李林.Matlab在大学物理实验数据处理中的应用. 大学物理实验，2008,26(1)：88

3 熊泽本.Excel 的回归函数在数据处理中的应用研究. 濮阳职业技术学院学报，2010(12):140

4 费业泰.误差理论与数据处理. 北京：机械工业出版社，2000.105

5 唐曙光.大学物理实验 . 北京：科学出版社，2011.126