静电场中的几个物理公式与其物理模型

董梅峰 宋新祥

(中国石油大学 山东 青岛 266555)

物理规律是对客观自然规律的描述，而对客观自然规律描述之前往往需要建立一个与其对应的物理模型.物理规律的描述一般有两种，一种是文字描述，另一种是数学描述，而物理规律的最终的也是最完美的描述形式是用数学公式来描述.所以物理规律的描述往往离不开数学公式，而一旦用数学公式来描述物理规律，这个数学公式就有了物理意义，公式中的各个物理量都有一定物理意义，其取值也要保证有物理意义，如果物理量的数学取值导致该公式没有物理意义了，此公式也就不成立了，此时该公式对应的物理模型发生了变化，所以需要寻找对应新模型的数学表达公式了.下面看几个典型的例子.

1 点电荷的电场强度公式的理解

点电荷激发的场的数学表达公式是静电场中的一个基本公式，即

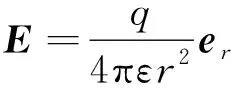
(1)

公式中的r是场点到点电荷的距离，在数学上如果r→0，则电场强度的大小E→∞，这在物理上是没有物理意义的.出现这种情况也就是说公式(1)不适用于r→0时所对应的物理模型，同时也说明了r→0时的物理模型不再是“点电荷”的物理模型了.回顾一下“点电荷”物理模型的建立条件，就不难理解当r→0时，带电体的形状和大小相对于场点而言就不能忽略了，此时带电体就不能视为“点电荷”物理模型了，所以上述公式不再适用了.

考虑到实际的带电体，当r→0时，场点在何处呢？不难理解此时场点已经到了带电体内部了.此时可以理解为物理模型由点电荷变为均匀带电的球体，如果其总的带电荷量为q，电荷体密度为ρ，可以用高斯定理很容易得到在均匀带电球体内、外的电场强度公式分别为

(2)

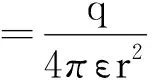
(3)

由式(2)可知当r→0时，E内→0，这样就有物理意义了.

2 无限长的均匀带电直线的电场强度公式的理解

无限长的均匀带电直线激发的场的数学表达式为

(4)

公式中的r是场点到无限长的均匀带电直线的垂线距离，在数学上如果r→0，则电场强度的大小E→，这在物理上也是没有物理意义的.此时考虑到实际的带电体，当r→0时，场点在何处呢？不难理解此时场点也已经到了带电体内部了.此时可以理解为模型变为无限长的均匀带电的圆柱体，如果其半径为R，单位长度上的带电荷量仍为λ，由高斯定理可求出其内、外的场强分布为

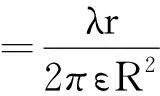
(5)

(6)

由公式(5)可知当r→0时，E内→0，这样就有物理意义了.

3 计算点电荷和无限长均匀带电直线激发的场的能量

3.1 点电荷激发的场的能量

由能量密度的体积分可得电场的能量，即

(7)

公式中D=εE，把点电荷的场强公式(1)代入公式(7)得

很明显上述积分结果又趋于无穷大，在物理上又没有物理意义了，而式(7)适用于任何带电体激发的场.此时同样回顾“点电荷”的物理模型的建立条件就明白，在上述积分公式中的积分下限为零时，此物理模型就不再是“点电荷”的物理模型了.如果考虑到实际情况，当r→0时，场点已经到了带电体内部了.把式(2)、(3)代入式(7)积分物理意义就明确了.

3.2 无限长均匀带电直线激发的场的能量

由式(7)可得一长度为L，可视为无限长的，线电荷密度为λ的无限长均匀带电直线激发的场的能量为

很明显上述积分结果也没有实际物理意义，从上述公式的积分下限看，考虑到实际情况，当r→0时，场点已经到了带电体内部了.上述带电“直线”的模型就不成立了；从上述公式的积分上限看，考虑到实际情况，当r→时，长度为L的直线就不能视为“无限长”的了.总之上述公式的积分上限和下限所描述的物理模型已不再是“无限长的均匀带电直线”的物理模型了，所以其积分结果也不是上述物理模型所激发的场的能量.

4 结论

通过以上数学公式与其所对应的物理模型的关系可以看出，物理模型不同，用数学语言描述其所遵循的物理规律也就不同，所以每个物理上的数学公式都有其物理意义，也就是描述了一个物理模型所遵循的物理规律.通过以上例子进一步明确了物理上数学公式的物理意义，以及在物理上建立物理模型具有重要的意义.有了建立物理模型的思路，这对物理规律的理解以及物理规律数学表达形式的理解都有很大的帮助.

参考文献

1 贾瑞皋．大学物理教程．北京：科学出版社，2009． 10～11

2 贾瑞皋．电磁学．北京：高等教育出版社，2003．13