巧用平动非惯性系解决高中物理力学问题

陈晓宇

(南通市启秀中学 江苏 南通 226001)

1 惯性系与非惯性系

由于选择的参考系不同，所观察到的物体的运动也会不同，凡是牛顿运动定律能够适用的参考系称为惯性参考系，反之，牛顿运动定律不适用的参考系称为非惯性参考系．一般情况下，相对地面静止或做匀速运动的参考系都可作为惯性系，而相对于地面做变速运动的参考系是非惯性参考系．

2 平动非惯性系及力学特征

(1)定义

系统相对惯性系以一定的加速度做平动，此参考系为加速平动非惯性系．如水平方向加速运动的汽车，竖直方向加速上升的电梯，沿光滑斜面下滑的物块等．

(2)力学特征：平移惯性力

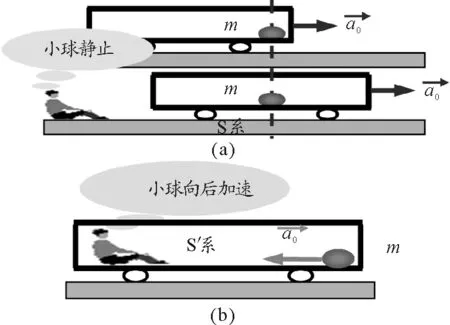
图1

如图1(a)所示，当汽车以加速度a0向前加速运动时，在惯性系(S系)中的观察者观察到光滑水平桌面的小球m处于静止状态，而在非惯性系(S′系)中的观察者观察到小球向后加速，而小球在水平方向上并未受到任何外力作用，牛顿运动定律此时不再适用．为了使牛顿运动定律在非惯性系中也能适用，可以人为地引进一个虚拟的惯性力f．如果非惯性系相对惯性系有平动加速度，那么只要认为非惯性系中的所有物体都受到一个大小为ma0，方向与a0的方向相反的惯性力f=-ma0，牛顿运动定律即可照用，证明如下.

设非惯性系S′相对惯性系S有平动加速度a0(牵连加速度)，质点相对于S系的加速度为a(绝对加速度)，质点相对于S′系的加速度为a′(相对加速度)，根据加速度合成公式，有

a=a′+a0

在惯性系S中牛顿运动定律成立，即

F=ma

其中F是作用在质点上的合外力，m是质点的质量．

在非惯性系S′中，为使牛顿运动定律成立，引入虚拟的惯性力f，使

F+f=ma′

联立则惯性力得

f=ma′-F=ma′-ma=ma0

3 利用平动非惯性系解决力学问题

【例1】如图2所示，匀速行驶的小车内，高为h的货架上放有一个小球，小车突然以加速度a做匀加速运动，小球落地点不是在货架正下方．求：小球落地点到货架下端的距离．

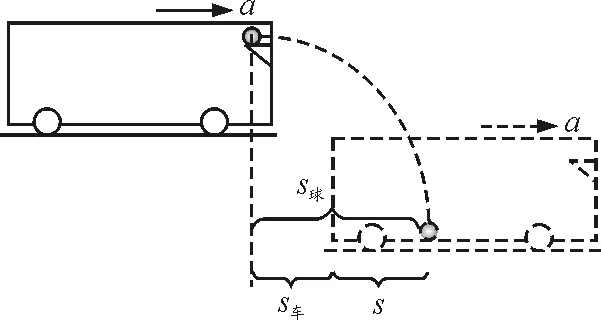
图2

解法一：如在惯性系中求解则有

s球=v0t

联立解得

解法二：在以匀加速运动的小车为参考系的非惯性系内，小球做匀加速直线运动，小球落地点到货架下端的水平距离如图3所示，为

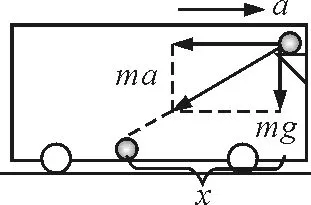
图3

【例2】高空中有4个小球，在同一位置同时以相同速率向上、向下、向左、向右被射出，不计空气阻力，图4是经过1 s后4个小球在空中位置的构图，其中正确图形是

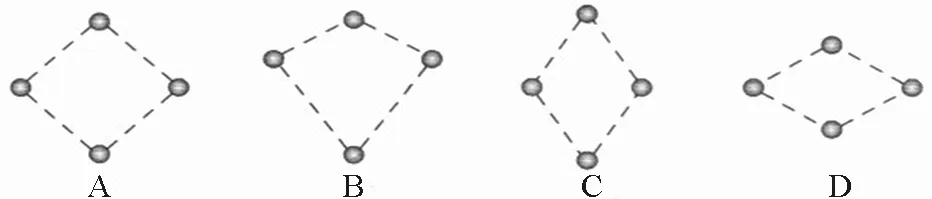
图4

解析：在以a=g的竖直向下的非惯性系中，小球向四个方向做匀速直线运动，所以答案为A．相比于惯性系而言，利用非惯性系求解要简单很多．

【例3】如图5(a)所示，一质量为M的光滑斜面A放在光滑的水平面上，斜面上放一质量为m的滑块B(可视为质点)．求滑块从斜面顶端由静止开始下滑到斜面底端所需的时间t(已知斜面倾角为θ，高为h).

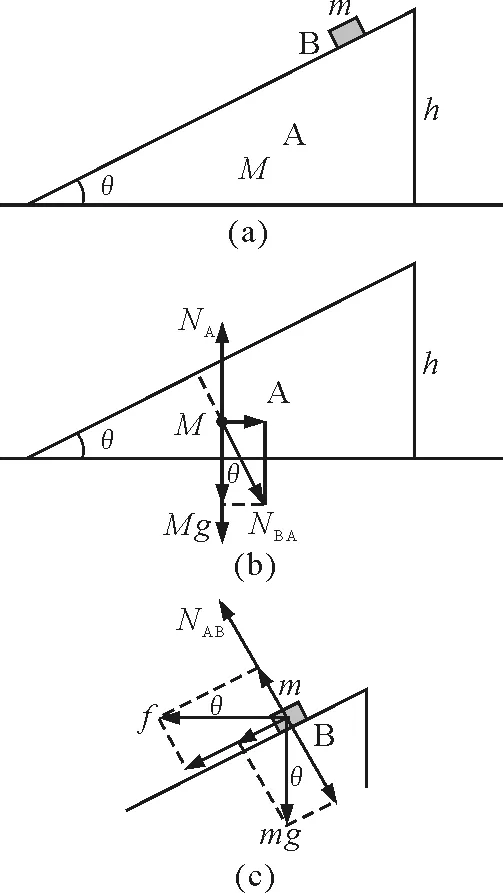
图5

解析：如图5(b)对斜面A受力分析可知斜面有水平向右的加速度为

(1)

选斜面为参考系(非惯性系)来研究滑块B的运动，为使牛顿运动定律成立，必须引入惯性力，故可认为滑块受3个力：重力mg，A对B的弹力NAB和水平向左的惯性力，如图5(c)所示.

f=maA

(2)

在斜面的参考系中，滑块在垂直于斜面的方向上是平衡的，由平衡条件得

NAB+fsinθ=mgcosθ

(3)

NAB和NBA是一对作用力与反作用力.联立式(1)、(2)、(3)解得

(4)

在斜面的参考系中，滑块在沿斜面的方向上做匀加速直线运动，由牛顿第二定律得

mgsinθ+fcosθ=ma相

(5)

联立式(1)、(2)、(4)、(5)解得

(6)

由运动学公式

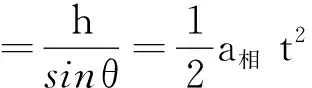
(7)

联立式(6)、(7)解得

显然在解决这道题的过程中，惯性力的引入带来了很大的方便．

4 总结

一般来说， 对于变速直线运动问题采用惯性力法只要在受力分析时加上平动惯性力就可以应用牛顿第二定律列式求解问题．实际问题中还要注意惯性力是虚拟力，没有施力物体，要跟真实力加以区分．在高中力学中还存在许多更复杂的问题， 如果能把惯性力很好地运用，相信一定会给解题带来更多的方便．