对一道经典试题的再思考

田胜安 刘治宏 张波

(张家界市民族中学 湖南 张家界 427000) (绵阳中学实验学校 四川 绵阳 621000) (包头市回民中学 内蒙古 包头 014040)

【例题】从地面以大小为v1的初速度竖直向上抛出一个皮球，经过时间t皮球落回地面，落地时皮球速度的大小为v2.已知皮球在运动过程中受到空气阻力的大小与速度的大小成正比，重力加速度大小为g.下面给出时间t的4个表达式中只有一个是合理的.你可能不会求解t，但是你可以通过一定的物理分析，对下列表达式的合理性做出判断.根据你的判断，你认为t的合理表达式应为

图1

此题作为考查学生物理基础知识及思维的经典例题常出现在各检测类的试卷中.但凡涉及此题的参考文献给出的解答均为排除法和极限法，有学生好奇该如何定量解答此题，在此，给出两种解法期望能对此题有个较深入的剖析以便利于学生的理解.

传统解法：考查各选项的量纲及考虑阻力为零的特殊情况,可轻易选出正确答案为选项C.

点评：此解法好处在于能快捷地选出正确选项，适宜用于各类检测中.譬如，解答近年某些高考选择题.但此法不利于学生对问题本质的掌握，在平常训练中不符合“打破沙锅问到底”类学生的需求.

解法1：对过程微元处理，分别写出上升段和下降段的运动表达式.设上升时间为Δt,下降时间为t2.

上升段有mgΔt+kviΔt=mΔvi

对其求和有mgt1+ks=mv1

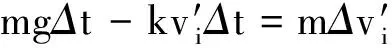
对其求和有mgt2-ks=mv2

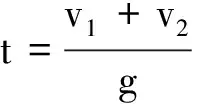
即答案为选项 C.

点评：运用微元法解答此题难度不大，对学生的物理及数学能力、知识要求不高，适合普通高中生掌握.但此法依旧不能挖掘出题设中皮球运动详情，似乎还是不够尽兴，下面再给出一种方法.

解法2：运用积分.首先假设空气的阻力系数为k，则物体所受空气阻力为f=-kv，选向上为正方向，可写出物体的整段运动方程如下(分段积分亦可)

(1)

(2)

对式(2)积分

(3)

(4)

读者似乎有些好奇，式(4)明显和正确答案不相同.但不相同并不意味着不相等.将式(1)改写为

(5)

对式(5)变形有

(6)

对式(6)积分得

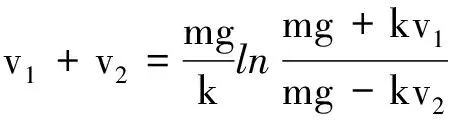
(7)

将式(7)代入式(4)中得

(8)

两答案是相等的只是形式不同.

点评：此法较为复杂，不建议对普通高中生进行推广，但对于有兴趣的学生，笔者觉得有介绍的必要.

另外,我们不妨将式(3)改写成任意时刻速度与时间之间关系的形式，即

(9)