整体式预应力葵花拱桥受力性能分析

康俊涛， 梁庆学,2， 周汉生

(1.武汉理工大学 土木工程与建筑学院， 湖北 武汉 430070;2.中国市政工程中南设计研究总院有限公司， 湖北 武汉 430010;3.利川市交通运输局， 湖北 利川 445400)

社会对桥梁属性的迫切需求，促使各种结构合理、造型美观的新型桥梁产生，如无桥台斜腿刚架桥[1]，悬带桥[2]等。葵花拱桥拱上建筑采用腹拱直接与主拱相连，取消了普通拱桥拱上建筑的立柱，从外形上看，是大拱上面叠小拱，使得桥梁立面富有层次感，并因其桥型轻盈、通透、美观、有韵律感，造型形似向日葵花瓣而得名[3]，也称“复拱桥”[4]，图1为一座典型葵花拱桥的效果图。

图1 葵花拱桥效果图

与非整体式系杆葵花拱桥相比，由于整体式预应力葵花拱桥桥面板与拱圈结构是一个结构整体，不仅采用腹拱代替常规空腹式拱桥的横墙或者立柱，使主拱在其拱脚至腹拱拱脚之间没有作用力直接作用，而且通过在整体式桥面板内布置预应力束来代替系杆平衡结构水平推力，大大增强了结构的整体受力性能，但也增加了结构的受力复杂程度，施工难度较大[5]。因此，为了更清楚地掌握整体式预应力葵花拱桥各主要设计参数对结构的受力影响，本文以一工程实例为背景，从如下几个方面进行研究：(1)主腹拱固接或铰接时结构控制截面受力分析；(2)主拱采用不同的矢跨比时结构控制截面受力分析；(3)腹拱采用不同的矢跨比时结构控制截面受力分析；(4)主腹拱固接或铰接时对主拱圈稳定性分析。

1 葵花拱桥的受力特点

葵花拱及单拱受集中力P作用，当集中力P作用于拱脚附近OA段时，对于葵花拱集中力作用于腹拱的CA段，而葵花拱主拱的OA段无直接作用力(如图2(a))，这决定了葵花拱的内力影响线在OA段与单拱有较大不同。例如当P作用于单拱拱脚时，此时对于具有理想拱轴线的单拱各截面的弯矩为零，而对应的葵花拱则是P作用于腹拱跨中C点，此时葵花拱主拱各截面的弯矩并不为零，可见葵花拱由于腹拱的作用，影响线与单拱不同。

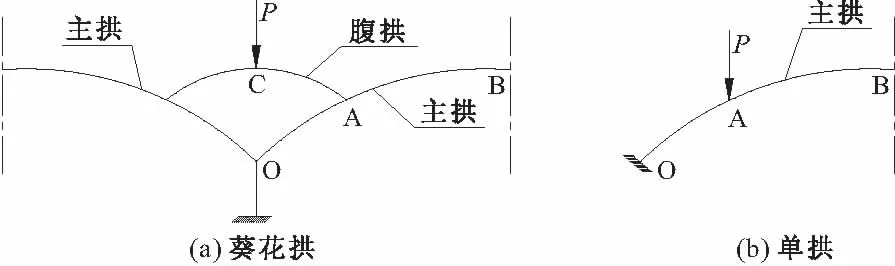
图2 葵花拱与单拱受力示意

图3所示为一主拱跨径为20 m，腹拱跨径为9 m的圆弧线葵花拱与单拱弯矩影响线(主、腹拱拱脚均按固接处理)。由于腹拱的作用，葵花拱主拱拱脚附近的弯矩影响线绝对值较大(单拱为零)，而单拱拱脚弯矩影响线绝对值在除拱脚附近外均比葵花拱大，这使得葵花拱在拱上填料及桥面系自重或活载作用下拱脚附近的负弯矩绝对值较大。腹拱拱脚对主拱的水平推力，对主拱拱脚截面产生拉力，使得主拱拱脚截面的轴力减小，从而拱脚截面的偏心距增大。可见不考虑拱上建筑联合作用时，腹拱对主拱拱脚的影响是不利的。腹拱拱脚对主拱的水平推力，对主拱拱顶截面产生压力，从而拱顶截面的偏心距减小，这对主拱拱顶截面的受力是有利的。

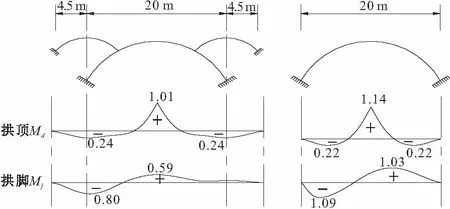
图3 葵花拱与单拱弯矩影响线比较

2 工程概况

如图4～5所示的整体式预应力混凝土葵花拱桥，桥跨组合为17.137 m+32.274 m+17.137 m，桥梁全长为73.669 m。中跨拱轴线为圆曲线，净跨径30 m，净矢跨比f/l=1/6.6，两边跨为曲梁形式，主拱上设圆曲线腹拱，腹拱计算半径为10.08 m，净跨径为10.2 m，主腹拱均为实腹式等截面，主拱截面厚0.6 m，腹拱截面厚0.3 m；整体式桥面板厚50 cm，桥面板内沿横向均匀布置11束Φs15.2纵向钢绞线，预应力束中心距桥面板下边缘10 cm，沿桥直线布置，预应力束张拉控制应力为1395 MPa。

桥全宽24 m，横向布置为2.5 m(人行道)+2.5 m(非机动车道)+14 m(机动车道)+2.5 m(非机动车道)+2.5 m(人行道)；桥梁设计荷载为：公路-I级，人群荷载为3.0 kN/m2。

图4 桥型布置及上构主要控制截面(cm)

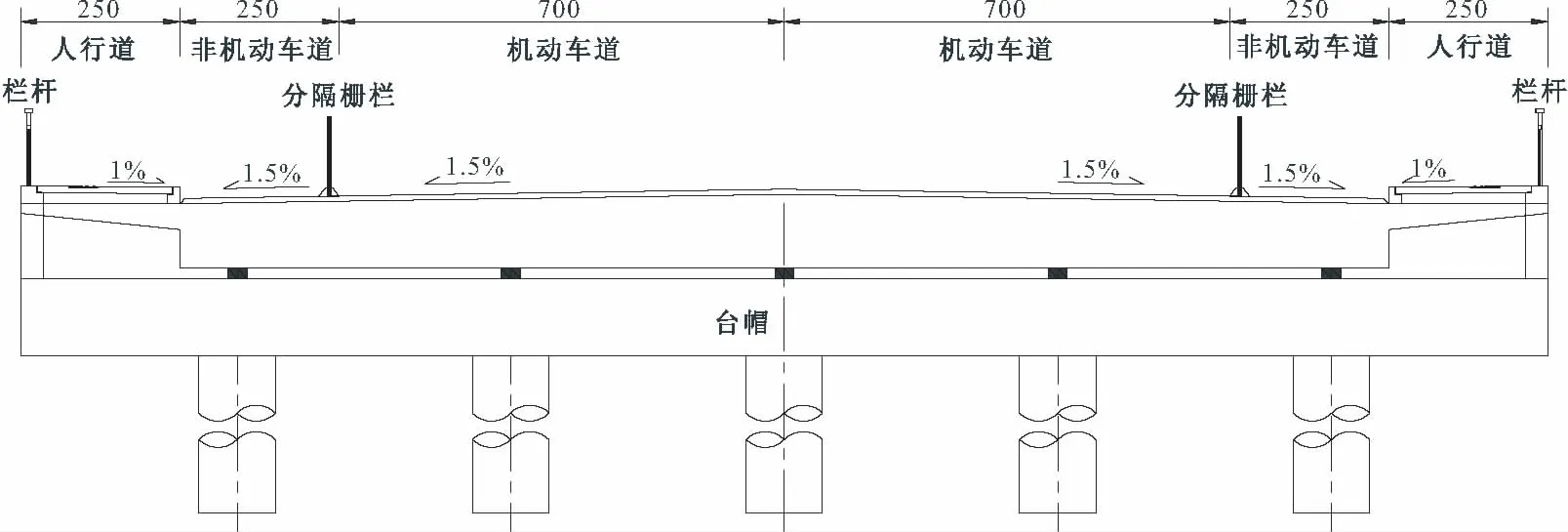
图5 A-A断面(cm)

3 葵花拱桥受力性能分析

3.1 桥梁结构计算模型

桥梁结构采用有限元分析软件Midas/Civil进行计算，全桥共划分为151个节点，142个单元，采用梁单元，其有限元模型如图6所示，计算时对主腹拱的连接方式分别处理成铰接和固接两种形式，并对主腹拱取不同矢跨比分别建立有限元模型。计算分析时对结构做如下假设和规定：(1)主腹拱均采用等截面的板拱，不考虑钢筋；拱圈及桥面板采用C40混凝土，弹性模量E=3.25×107kN/m2，承台采用C30混凝土，弹性模量E=3.00×107kN/m2，混凝土泊松比均取ν=0.2；(2)用直梁单元模拟曲线拱圈[6]；(3)主腹拱与上部桥面板、主拱与承台连接均采用弹性连接模拟；两端桥台处采用一般支承模拟桥梁支座，桥墩处根据桩土相互作用按实际情况采用一般弹性支撑模拟基础弹性刚度。

图6 桥梁有限元模型

3.2 主腹拱连接方式的影响

桥梁承受恒载和活载作用，恒载主要为结构自重和桥面板预应力，活载主要为汽车和人群荷载，在此主要对恒载和活载作用下的截面内力进行对比分析，主拱圈控制截面位置如图4所示，计算结果如图7～10所示。腹拱控制截面位置依次为1-腹拱圈左拱脚；2-腹拱L/4处；3-腹拱L/2处；4-腹拱3L/4处；5-腹拱右拱脚，计算结果如图11～14所示。

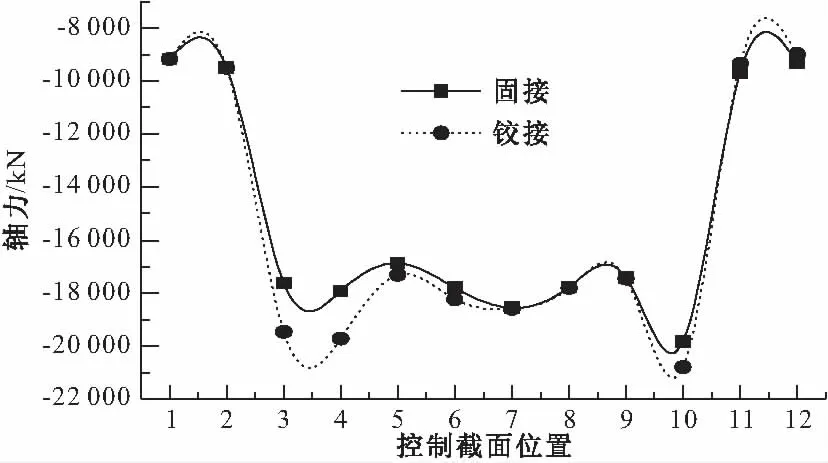
图7 主拱恒载轴力对比

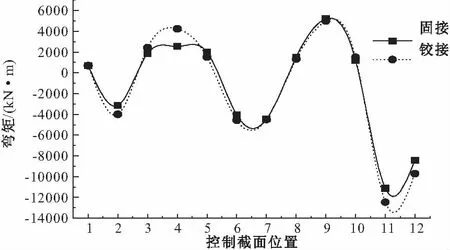
图8 主拱恒载弯矩对比

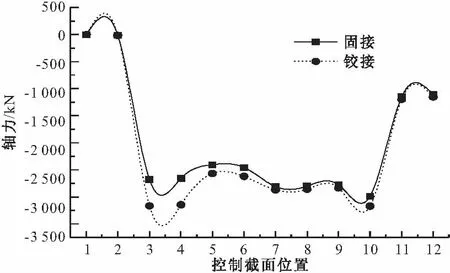
图9 主拱活载轴力对比

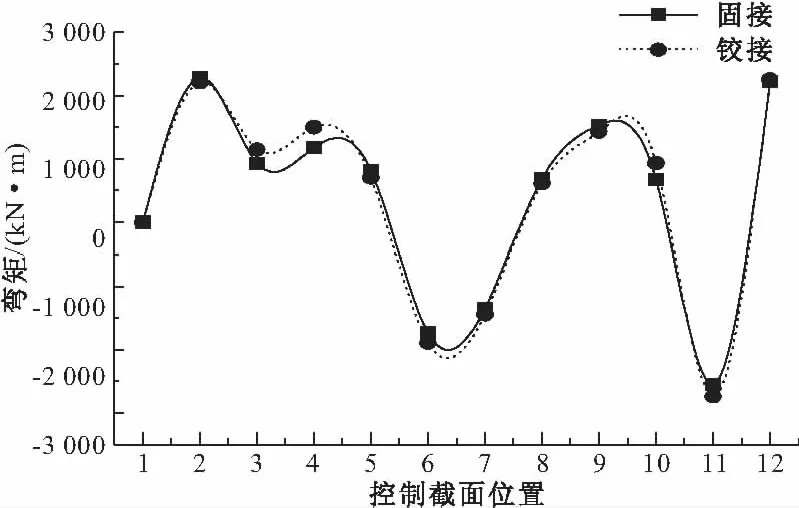
图10 主拱活载弯矩对比

从图7、9可知：铰接时主拱各控制截面的轴力值基本都大于固接时的轴力值，恒载轴力值在边孔L/2截面处增幅最大，为10.5%，活载轴力值在边孔主腹拱连接处增幅最大，为18.3%。

从图8、10可知：在主腹拱采用固接与铰接条件下，主拱恒载和活载产生的弯矩，除主腹拱连接处(即图4对应的截面4)弯矩变化幅度较大，恒载弯矩值铰接时比固接时增大了68.2%，主拱其余控制截面的弯矩变化幅度很小，几乎一样。

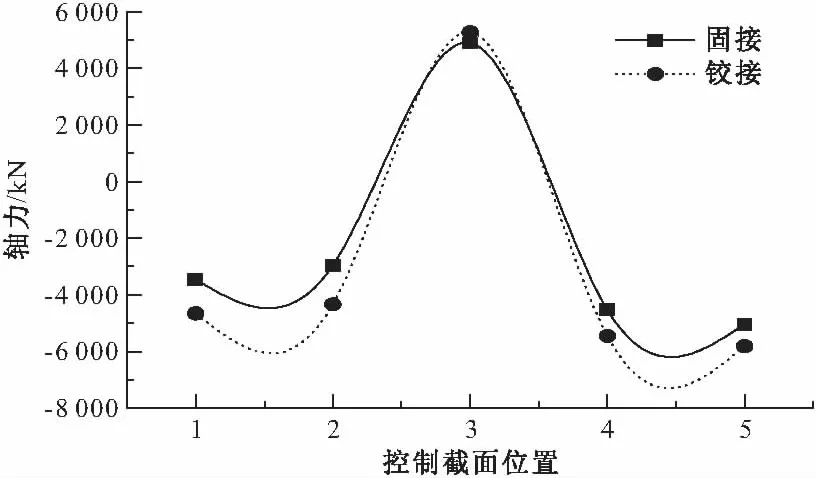
图11 腹拱恒载轴力对比

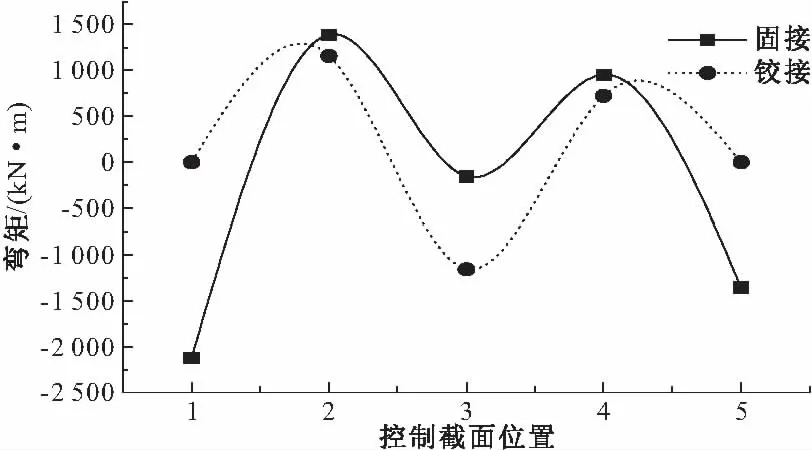
图12 腹拱恒载弯矩对比

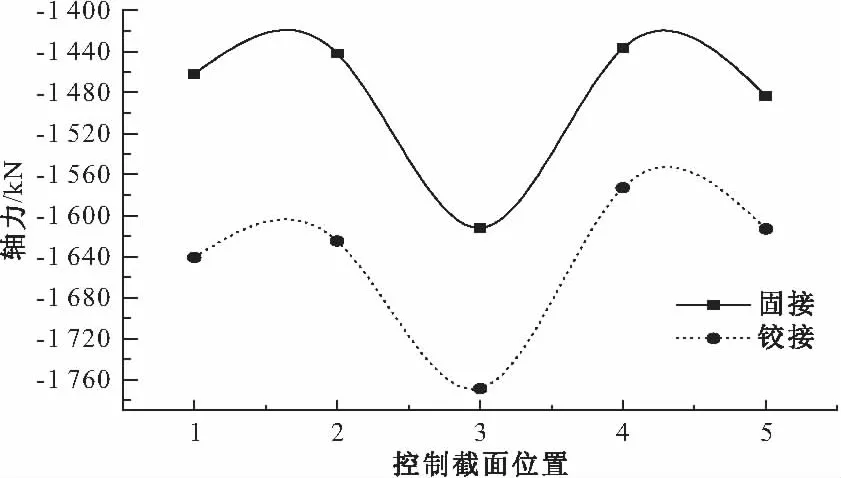
图13 腹拱活载轴力对比

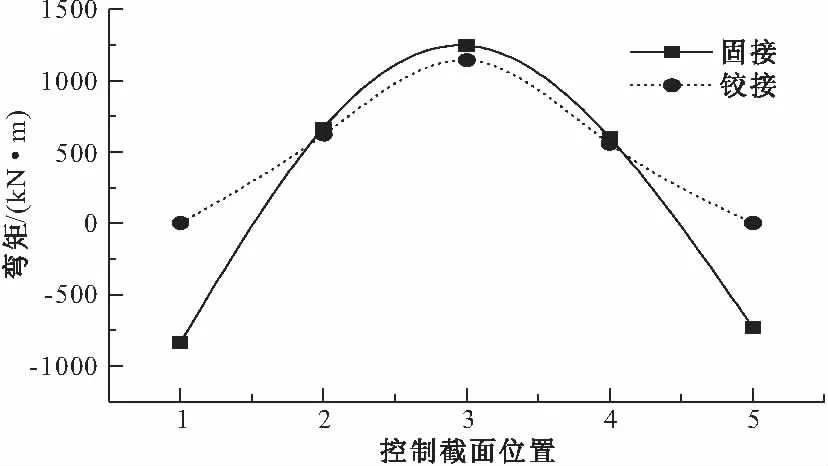
图14 腹拱活载弯矩对比

从图11、13可知：主腹拱采用铰接时腹拱各控制截面的轴力值均比采用固接时大，其中恒载作用下腹拱L/4截面处轴力值增大了46.3%。

从图12、14可知：在主腹拱分别采用固接与铰接条件下，腹拱L/2处恒载弯矩值变幅最大，铰接时的弯矩值是固接时的6.5倍；腹拱各控制截面的活载弯矩值除拱脚截面外变幅均不大，最大为8.1%。

由以上分析可以得出，从受力角度考虑主腹拱连接方式宜采用固接，同时，在施工上主腹拱固接更容易处理。

3.3 主拱矢跨比的影响

主腹拱连接方式采用固接，腹拱矢跨比取1∶6(腹拱设计矢跨比)，主拱矢跨比分别取1∶8、1∶7、1∶6.6(主拱设计矢跨比)、1∶6、1∶5时，主腹拱各控制截面在恒载和活载作用下的内力结果如图15～18所示。

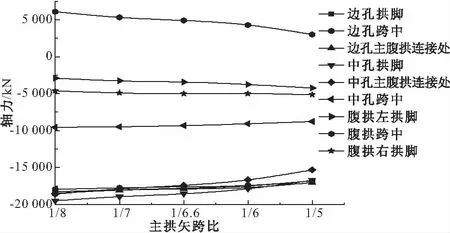
图15 恒载轴力对比

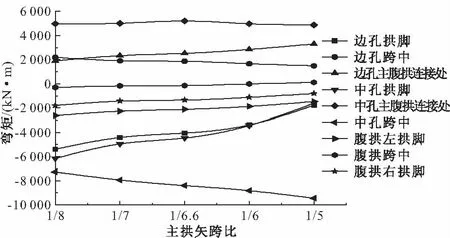
图16 恒载弯矩对比

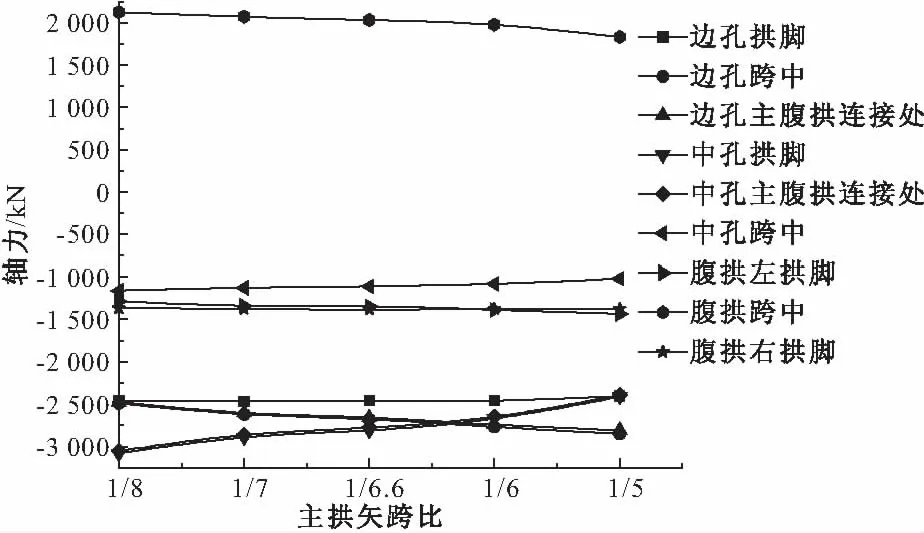
图17 活载轴力对比

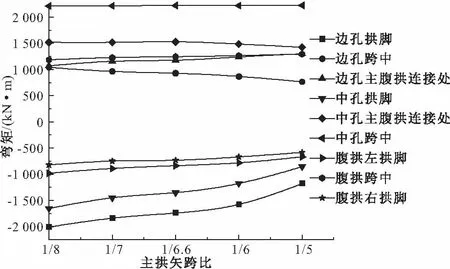
图18 活载弯矩对比

从图15、17可知：恒载作用下主拱各控制截面的轴力值均随主拱矢跨比的增大而减小，减幅在10%左右，而中孔主腹拱连接处因腹拱拱脚集中力的作用，减幅最大，达到17.7%。恒载作用下腹拱左右拱脚截面的轴力值随主拱矢跨比的增

大而增大，其中腹拱左拱脚截面的轴力值增大了1350 kN，腹拱跨中截面的轴力值随主拱矢跨比的增大而减小，主拱矢跨比1∶5时的轴力值比1∶8时小了3105 kN。主腹拱各控制截面的活载轴力值在数值上均比恒载轴力值小得多，且随主拱矢跨比增大，活载轴力值除中孔拱脚(减小671 kN)和中孔主腹拱连接处(减小663 kN)外，其余各控制截面的轴力值变化较小。

从图16、18可知：主拱矢跨比主要对主拱边孔、中孔拱脚和中孔跨中截面弯矩值有较大的影响，对其他各控制截面弯矩值影响较小。恒载作用下主拱边孔和中孔拱脚截面的弯矩值随主拱矢跨比的增大而减小，最大减幅为73.7%，恒载作用下中孔跨中截面的弯矩值随主拱矢跨比的增大而增大，增幅为29.8%，且绝对数值均较大。活载弯矩值除边孔拱脚(减小830 kN·m)和中孔拱脚(减小798 kN·m)外，其余各控制截面的弯矩值变化均较小。因此主拱矢跨比变化主要对恒载弯矩值有较大的影响。为使各控制截面受力相对较好，建议主拱矢跨比取值在1∶7～1∶6之间。

3.4 腹拱矢跨比的影响

主腹拱连接方式采用固接，主拱矢跨比取1∶6.6不变，腹拱矢跨比分别取1∶8、1∶7、1∶6、1∶5、1∶4时，主腹拱各主要控制截面在恒载和活载作用下的内力结果如表1和表2所示。

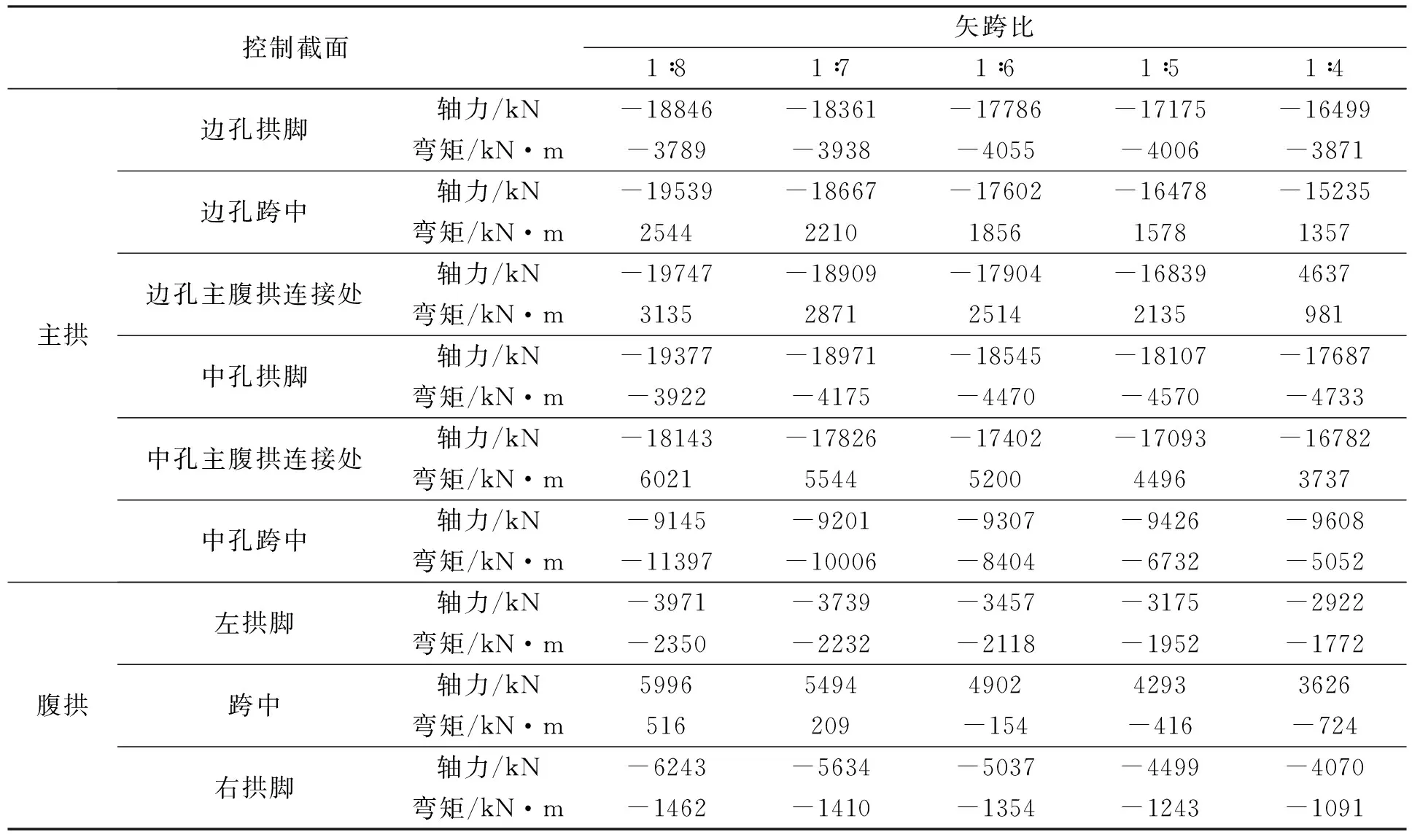
表1 腹拱采用不同矢跨比时主腹拱恒载内力

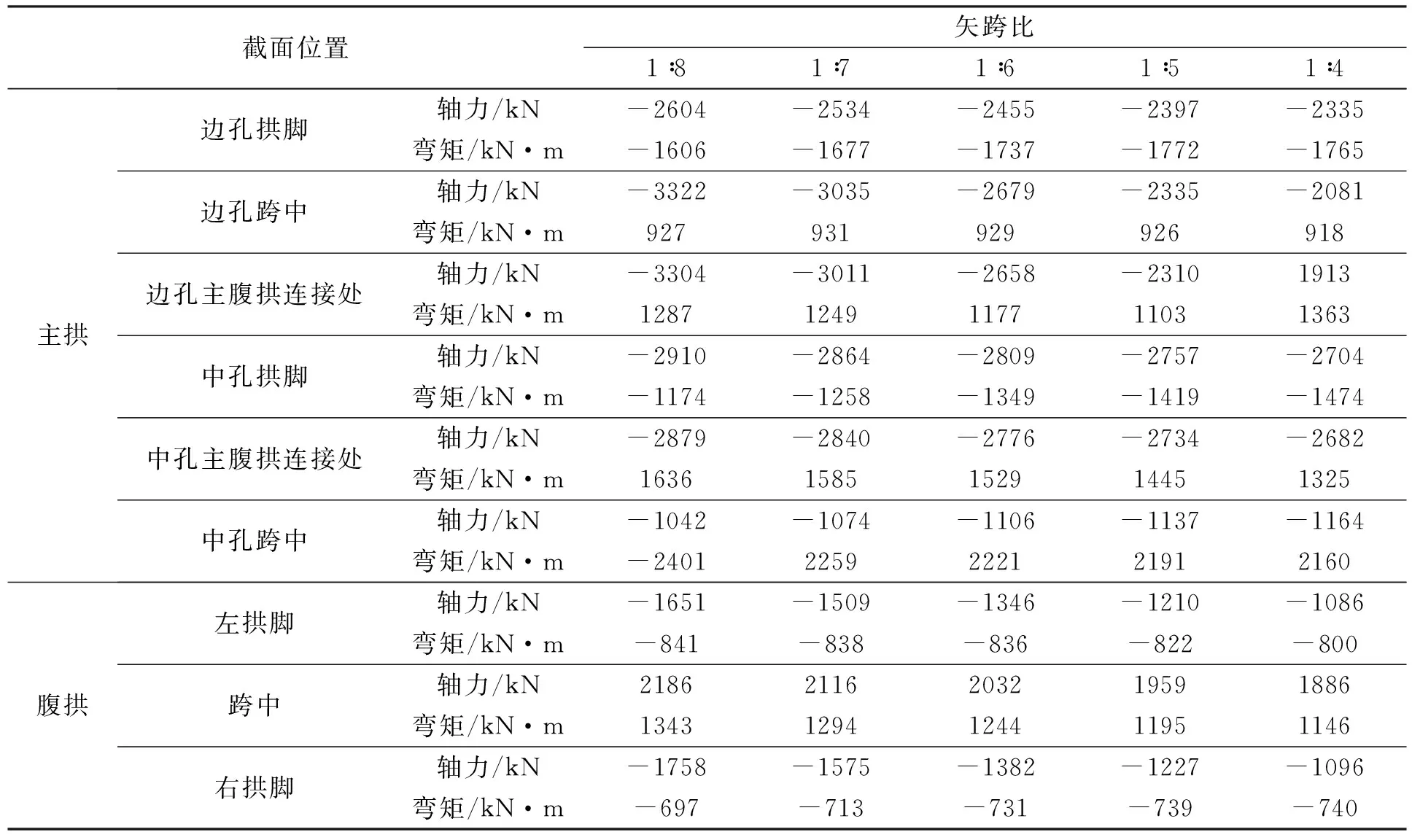
表2 腹拱采用不同矢跨比时主腹拱活载内力

从表1和表2可知：

(1)从整体上看，主腹拱各控制截面在恒载和活载作用下的轴力值和弯矩值大都随着腹拱矢跨比的增大而减小。因此，腹拱的矢跨比越大对主腹拱结构受力越有利。这点从直观上可以理解为，当腹拱矢跨比取无穷大，即腹拱跨径趋近于零时，腹拱对主拱无水平推力作用，这时腹拱的作用就相当于常规空腹式拱桥的立柱，腹拱对主拱只有竖向作用。

(2)腹拱矢跨比由1∶5变化至1∶4时，边孔主腹拱连接处恒载轴力值由-16839 kN(压力)变为4637 kN(拉力)，活载轴力值由-2310 kN(压力)变为1913 kN(拉力)；恒载弯矩值也发生突变，变幅达117.6%。因此，腹拱矢跨比不宜大于1∶5。

(3)腹拱矢跨比由1∶7变化至1∶8时，中孔跨中截面的弯矩值发生剧变，由2259 kN·m变为-2401 kN·m。中孔跨中截面弯矩值发生质变。因此，腹拱矢跨比不宜小于1∶7。

3.5 拱圈稳定性分析

整体式预应力葵花拱桥的主、腹拱圈均为压弯构件，存在稳定性问题，需进行分析。在工程应用中，第一类稳定问题的求解较第二类稳定问题容易，因此其计算方法被广泛应用，采用第一类稳定计算方法进行稳定计算时，均要求有较大的稳定系数，在拱桥计算中一般取4～6[7]。

采用Midas/Civil对主腹拱分别采用固接和铰接时的拱圈第一类稳定问题进行计算，其在恒载作用下的稳定特征系数如表3所示。

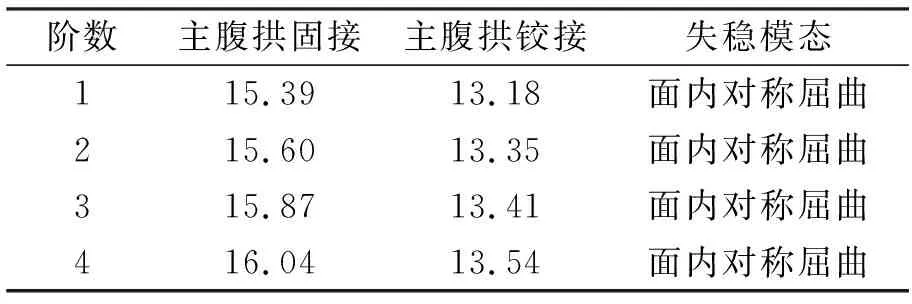
表3 稳定特征系数

由表3可知，无论主腹拱采用固接还是铰接，结构都有较高的稳定系数，整体稳定性较好，且固接时结构的稳定性比铰接时更好。

3.6 设计参数的取值

根据以上对整体式预应力葵花拱桥各结构参数的分析，本桥设计时主腹拱之间采用固接，主拱矢跨比为1∶6.6，腹拱矢跨比为1∶6。桥梁竣工后，经权威机构检测各项指标均在规范规定的范围之内，表明结构受力性能良好，结构参数合理。

4 结 论

(1)从控制截面受力状况和施工方便角度讲，整体式预应力葵花拱桥主腹拱连接方式宜采用固接。

(2)整体式预应力葵花拱桥腹拱矢跨比不宜过小或者过大，其腹拱最优矢跨比宜在1∶7～1∶5之间。

(3)主拱矢跨比对中孔主腹拱连接处和腹拱拱顶的恒载轴力值以及主拱边孔、中孔拱脚和中孔跨中截面的恒载弯矩值影响相对较大。为使结构各截面受力相对较好，建议主拱矢跨比在1∶7～1∶6之间。

(4)拱圈稳定性分析表明，无论整体式预应力葵花拱桥主腹拱是采用固接还是铰接，拱圈都不会发生失稳，表明整体式预应力葵花拱结构整体稳定性好，且主腹拱固接时拱圈的稳定性优于铰接时。

(5)本文对整体式预应力葵花拱桥各设计参数的分析具有普遍意义，可为类似中小跨度葵花拱桥的推广应用提供一定的理论参考。

[1] 王国鼎. 无桥台斜腿刚架桥：适用、经济、美观的新桥型[J]. 公路，2000,(3) :26-29.

[2] Tony Sanchez.San Diego stress ribbon bridge sets new world record [J]. Proceedings of the Institution of Civil Engineers-Civil Engineering. 2010, 163(4):162-169.

[3] 王新生，辛玉升.钢筋混凝土葵花拱桥有限元分析[J].公路交通科技(应用技术版)，2009,(1):129-132.

[4] 王 丰.钢筋混凝土复拱桥结构分析[D].长安：长安大学，2004.

[5] 金文成，赵弘尧，白金增，等.预应力葵花拱桥结构设计[J].城市道桥与防洪，2012,(1):45-47.

[6] Yang Y B, Kuo S R, Yau J D. Use of straight-beam approach to study bucking of curved beams[J]. Journal of Structural Engineering, 1991, 117(7): 1963-1978.

[7] 顾安邦，孙国柱.公路桥涵设计手册—拱桥(下册)[M].北京：人民交通出版社.1997.