车-线-桥耦合单元组合长度影响分析

杨宏印， 杨秀华， 陈志军， 张海龙， 黄 雯

(1.华中科技大学 土木工程与力学学院， 湖北 武汉 430074；2.湖北工程学院 城市建设学院， 湖北 孝感 432000)

高速铁路和公路的发展给人们的生活和工作带来了极大的方便和快捷，同时也产生了一些工程技术问题。作为铁路领域重要的技术难题，车-桥耦合相互作用一直是土木工程中人们关注和研究的热点[1],而有限元法是最为广泛采用的方法之一[2，3]。文献[4，5]提出了各种不同的车-桥相互作用单元，但都忽略了轨道结构的影响，而轨道结构能对系统产生很大的影响[6]，利用弹性系统动力学总势能不变值原理[7，8],文献[9]推导了车-线-桥耦合动力分析时变矩阵方程，对比分析了单轴和四轴车辆模型的影响。采用相同长度的轨道和桥梁单元，根据车辆、轨道和桥梁单元垂向运动方程及轮轨约束条件，文献[10]提出了车-轨道-桥耦合单元，分析了不同轨道结构的影响。考虑双层线路模型，文献[11]推导了不等长度的轨道-桥梁耦合单元，并研究了采用较长桥梁单元对系统响应的影响。以上这些分析模型都基于车轮密贴假设，即车轮始终与下部结构保持接触，而实际轮轨相互作用是一个高速移动接触-碰撞-滑移的非线性过程，在不平顺或车辆速度非常高的情况下，车轮瞬时脱离是存在的[1]。

本文针对单层线路模型，考虑到轨道直接承受和传递轮轨激励，且其刚度和质量远小于桥梁，故采用较短的轨道单元，提出了任意长度组合的轨道-桥梁耦合单元。然后采用Hertz弹性接触，允许轮轨脱离发生，结合车辆方程推导了车-线-桥耦合系统的动力方程，给出了系统方程组装和求解思路，并采用MATLAB语言编制了相应计算程序。再结合我国现有铁路线路进行分析，讨论了所提耦合单元的准确性和有效性。最后针对不同轨道单元长度进行车-线-桥耦合响应对比分析，给出了轨道单元长度的合理取值范围，并分析了轨道随机不平顺对系统响应的影响，得到了一些有益的结论。

1 任意长度组合的轨道-桥梁耦合单元推导

图1为车-线-桥耦合系统模型，采用10D车辆模型，通过Hertz弹簧模拟轮轨接触。考虑连续弹性支承梁轨道模型，采用平面梁单元模拟轨道和桥梁，并根据计算要求细分轨道单元，得到任意长度组合的轨道-桥梁耦合单元，如图2所示。

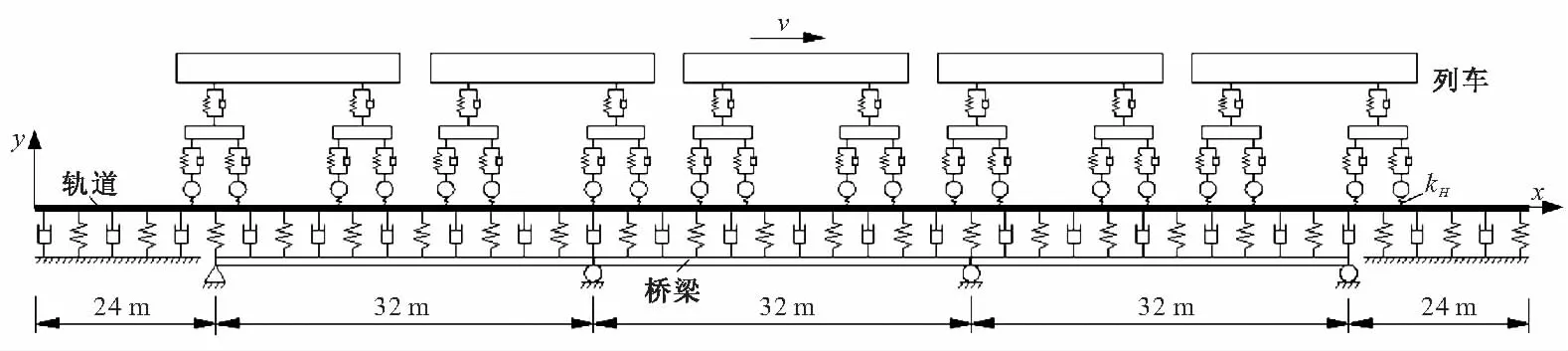
图1 车-线-桥耦合系统模型

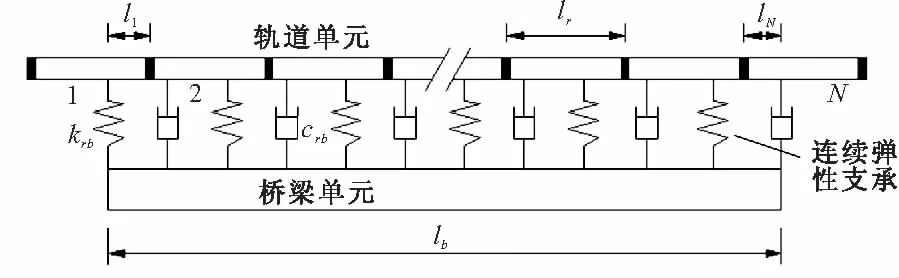
图2 任意长度组合轨道-桥梁耦合单元

桥梁结构采用Rayleigh阻尼，其单元动力方程可表示为：

(1)

式中，[M]、[C]和[K]分别为质量、阻尼和刚度矩阵；{q}为节点坐标；[N]为Hermite插值形函数。

轨道传给桥梁的分布力可表示为：

(2)

式中，krb和crb分别为连续弹性支承刚度和阻尼；ymr和yb分别为x处轨道和桥梁位移，可通过各自节点坐标插值得到。

由图2可见，桥梁单元上共有N个轨道单元，不失一般性，仅对单个轨道单元的影响进行推导。将式(2)代入式(1)，并沿第m(=1,2,…，N)个轨道单元积分，整理可得：

(3)

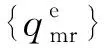
(4)

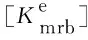
式(3)即为图2所示单个轨道单元下桥梁单元动力方程，这里只需令l1=lN=lr及N=1便得到等单元长度下相应动力方程。

同理可得图2所示无车轮作用下第m个轨道单元动力方程：

(5)

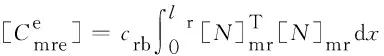
由式(3)和式(5)便可得到图2所示任意长度的轨道-桥梁耦合单元动力方程，具体表达式为：

(6)

由式(6)及形成矩阵的“对号入座”法则[13]，便可组装得到轨道-桥梁结构动力方程：

(7)

2 车-线-桥耦合系统分析

由上节得到的轨道-桥梁结构动力方程，考虑轮轨Hertz接触模型，再结合车辆动力方程[12]，便可得到车-线-桥耦合系统动力方程：

(8)

式(8)中，Kcr、Krv、Kvr、Fcr和Fcv为与轮轨接触有关的项，是时变的，而其他项均是时不变的。如图3，在求解时可先由式(7)和文献[12]组装时不变部分，作为初始方程，然后在每个积分步根据时间叠加时变部分便可得到系统动力方程，采用Newmark-β方法直接积分求解，不需迭代。

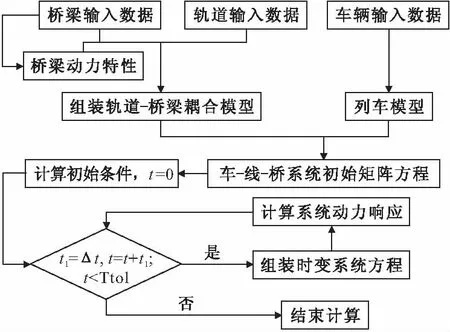
图3 车-线-桥耦合系统组装和计算流程

编制了相应MATLAB计算程序，对图1所示5辆车作用下3跨简支箱梁桥耦合系统进行动力分析。参照我国现有铁路线路，桥梁结构参数如下：跨距L=32 m；弹性模量Eb=34.5 GPa；惯性矩Ib=11.1 m4；单位长质量mb=43628 kg/m；阻尼比ζ=0.02。桥梁一阶频率为4.6 Hz，理论共振车速为108 m/s，文中考虑v=100 m/s接近共振车速。Hertz弹簧刚度采用2.8×109N/m[15]，车辆和轨道模型参照文献[9]，考虑美国6级轨道随机不平顺[1]，其模拟样本如图4。

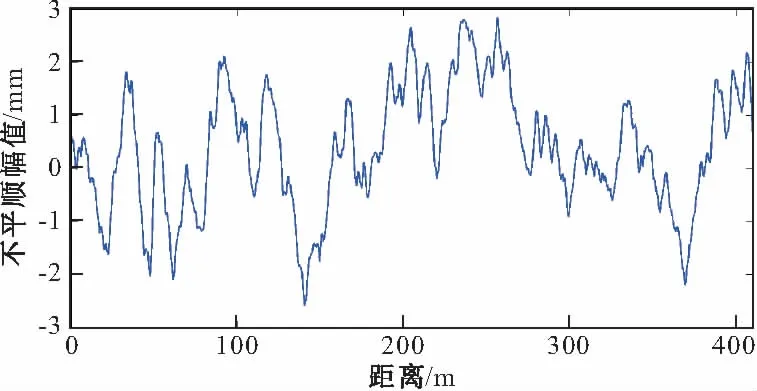
图4 竖向轨道不平顺样本

2.1 不同长度组合的轨道-桥梁耦合单元对比分析

为验证图2所示耦合单元的计算精度和效率，对比分析如下3种单元长度组合：

组合1：轨道单元采用0.8 m，桥梁单元采用4 m；

组合2：轨道和桥梁单元长度均采用0.8 m；

组合3：轨道和桥梁单元长度均采用4 m。

图5～8为不考虑轨道不平顺时动力响应时程结果。图5和6分别为中跨跨中桥梁位移和加速度时程，可以看到每辆车依次通过所激发的周期性响应，各种组合下竖向位移响应均一样。而对桥梁加速度响应而言，组合1和2所得结果完全一致，说明采用较长的桥梁单元同时将轨道单元细划，对桥梁响应影响很小；而组合3和1之间存在显著的不同，前者最大值(0.46 m/s2)明显大于后者(0.35 m/s2)，说明轨道单元长度对桥梁响应影响很大。图7为跨中轨道相对于桥梁位移时程图，可见车辆定距和轴距所产生的连续周期性激扰导致了轨道支点处的周期性强迫振动，组合1和2所得结果相同；而组合3所得结果明显不同于组合1，说明当采用较长的桥梁单元时，为得到正确的结果，应对轨道单元进行细分。图8为中间车辆过桥时车体加速度对比图，亦可见组合1和2所得结果符合一致，而组合3所得结果与组合1有明显不同。

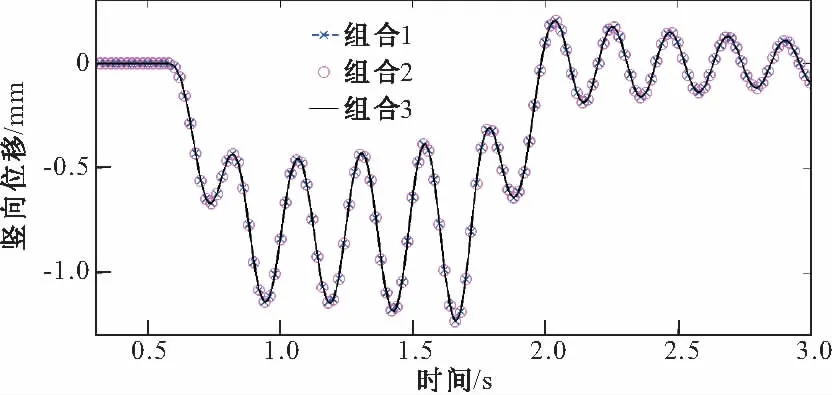
图5 桥梁跨中位移对比

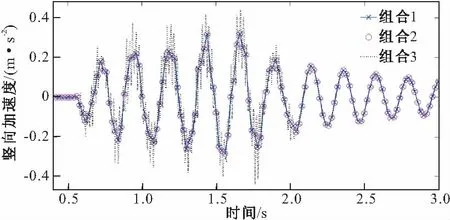
图6 桥梁跨中加速度对比

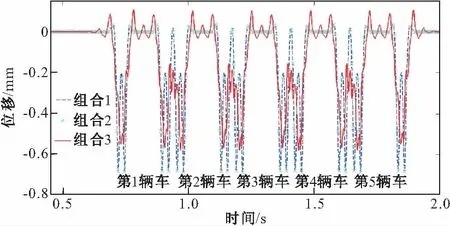
图7 轨道相对位移对比

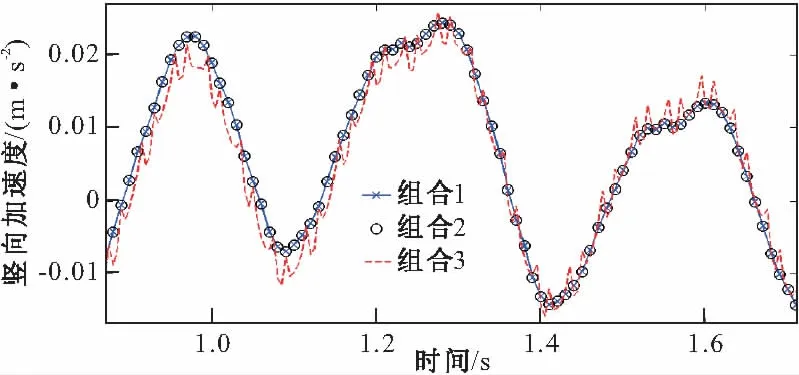
图8 车体加速度对比

表1列出了部分动力响应最大值，计算中发现轨道随机不平顺激励下，组合3中轮轨出现持续脱离，计算不稳定，故未列相应结果。由表1可见，光滑和不平顺激励下组合1和2所得结果均非常一致。而光滑时，组合3所得结果与组合1有显著区别，前者最大轮轨接触力为后者的1.26倍，但轨道最大加速度却为后者的35.7%。这是由于转向架固定轴距只有2.5 m，而组合3轨道单元过大(4 m)，会同时承受2个车轮作用，使动力响应结果不准确。同时可以发现轨道不平顺的影响非常大，可使车体最大加速度增加4.5倍，在进行行车舒适性分析时不可忽略。

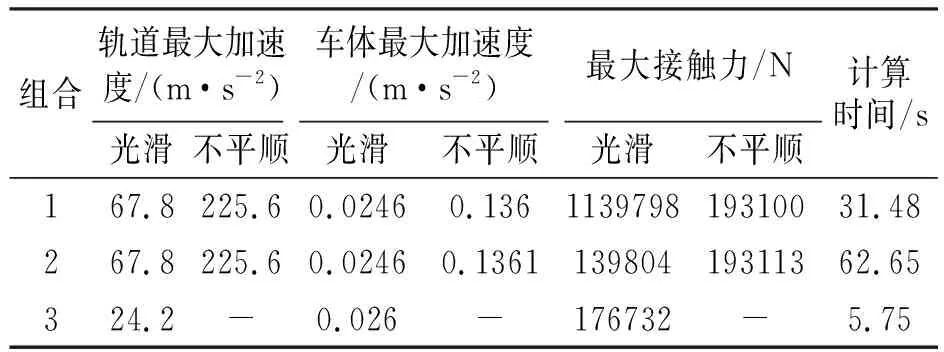
表1 动力响应最大值对比

由前面分析可知，相较于组合3，组合1和2均具有较高的计算精度；组合1和2的总自由度分别为446和658，前者计算时间仅为后者的一半，故前者在模型建立和计算方面具有更高的效率。因此，合理长度组合的轨道-桥梁耦合单元是准确和有效的。

2.2 轨道单元长度的影响

轨道结构直接承受和传递轮轨激励，其单元长度可对系统分析结果产生重要的影响。应用所提出的耦合单元，桥梁单元长度均采用4 m，对表2所示7种典型轨道单元长度进行对比分析，以研究车-线-桥耦合有限元分析中轨道单元的合适长度。而轨道不平顺激励下，工况7轮轨持续脱离，计算不稳定，故未列相应结果。

表2 轨道单元长度

图9为中跨跨中处桥梁和轨道最大位移对比图，可见前6个工况下结果基本一致，说明轨道单元长度对桥梁和轨道位移响应影响较小；桥梁最大位移均小于轨道，为后者的65%左右。同时可见考虑轨道不平顺会使最大位移响应减小，可使桥梁减小到原来的95%，而轨道减小到原来的91%，说明轨道不平顺激起高频的振动。图10为中间车辆前轮最大接触力对比图，可见相同轨道状态下前5个工况下响应相差不大；轨道不平顺影响很大，可使其结果增大到1.4倍，在列车脱轨和轮轨损伤分析中不可忽略；而光滑下工况7和不平顺下工况6所得结果明显偏大，使这两种工况变得不合理。图11为轨道光滑时不同轨道单元长度下中间车辆前轮接触力时程，可见轮对进入计算区域时，存在一个明显的冲击效应；工况5(1 m)经较短过渡区域，很快稳定到静轴载附近，而工况7(2 m)整个过桥过程均振荡剧烈。图12为不平顺对中间车辆车体加速度影响图，可见不平顺能明显增大其响应。

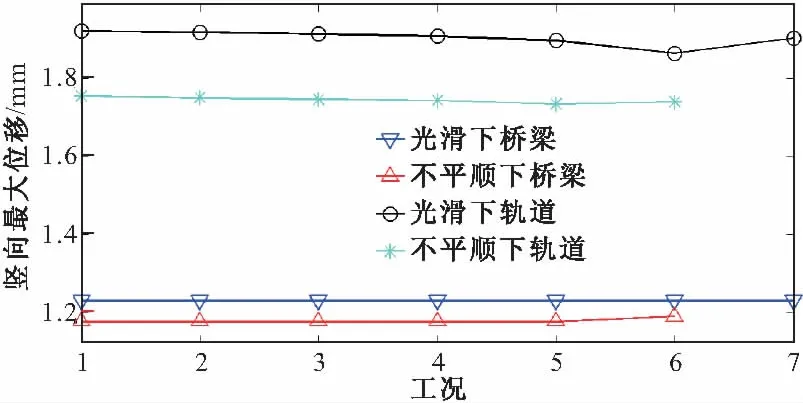
图9 桥梁和轨道最大位移对比

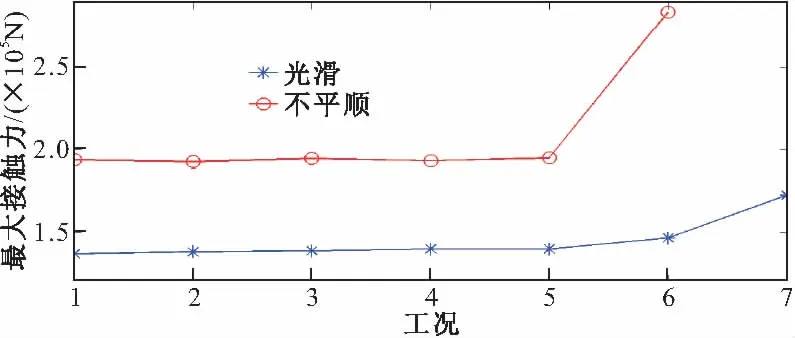
图10 最大接触力对比

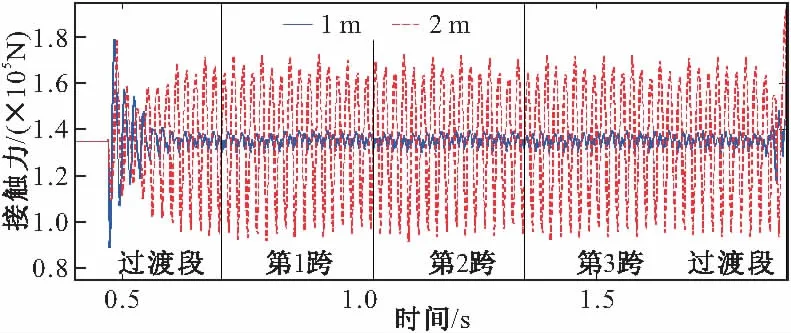
图11 不同轨道单元长度接触力对比

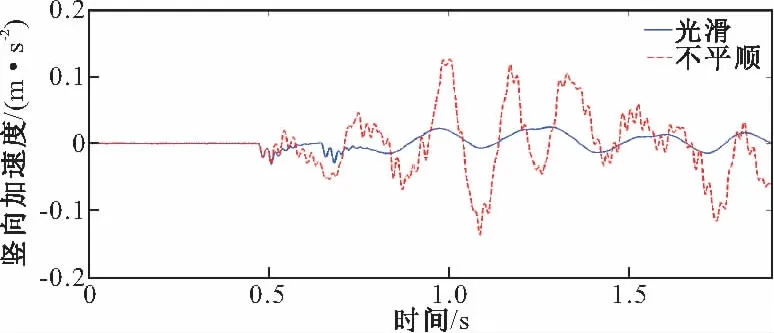
图12 不平顺对车体加速度影响

表3列出了部分响应最大值及各工况计算时间，各工况轨道加速度结果离散性很大，要得到其准确值需进一步分析。尽管工况7计算时间最短，但动力响应和其他工况有明显差异，精度较差；工况1轨道划分最精细，但计算精度并没有明显提高，而计算时间却明显呈指数增加趋势；轨道不平顺下，虽然工况6最大接触力明显大于工况1～5(见图10)，但桥梁和车体最大加速度等响应最大值并没有太大区别，说明应将列车、轨道和桥梁作为一个大系统来进行综合分析评价。同时可见轨道不平顺可使桥梁最大加速度增加近2倍。

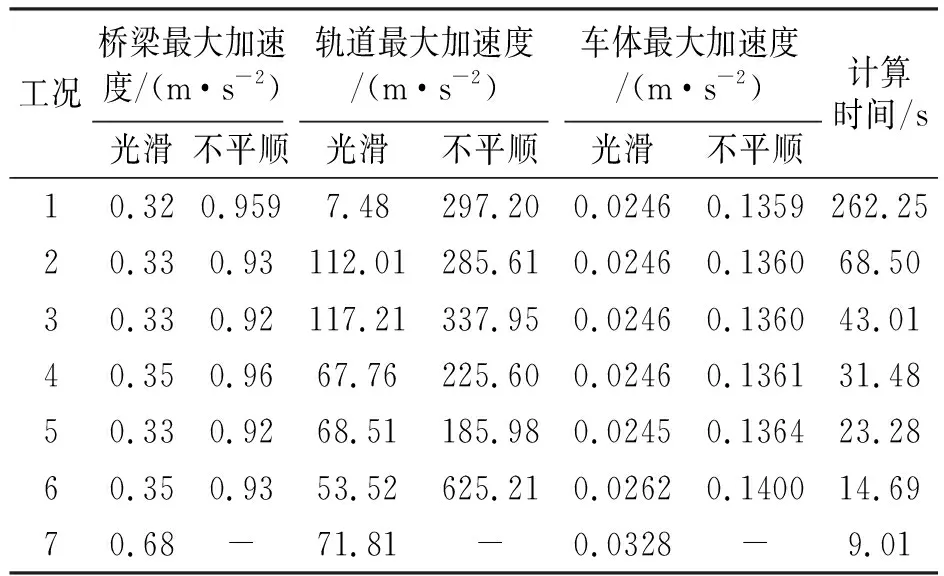
表3 动力响应最大值和计算时间

因此，综合考虑计算精度和效率，轨道单元的合适长度范围为0.5～1 m，且列车最小轴距间单元数不应少于2个。考虑到我国一般线路轨枕间距为0.568 m或0.545 m，新建时速200 km/h以上高速铁路为0.6 m[14]，建议实际分析时取轨枕间距为轨道单元长度。

3 结 论

针对车-线-桥耦合有限元分析建模复杂和计算量大的问题，提出了任意长度组合的轨道-桥梁耦合单元，并推导了其动力方程；然后采用Hertz接触模型，结合车辆方程推导了车-线-桥耦合系统的动力方程，并给出了系统方程组装和求解思路；再结合我国现有铁路线路进行分析，讨论了所提耦合单元的精度和效率；最后对多种轨道单元长度进行对比分析，并考虑轨道不平顺的影响，研究了其合适取值范围，得到了如下结论：

(1)轨道单元长度能对系统动力响应产生很大影响，甚至会使计算无法进行；合理长度组合的轨道-桥梁耦合单元能达到很好的计算精度和效率。

(2)轨道不平顺对系统影响很大，可使车体加速度和轮轨接触力分别增大4.5倍和40%，在行车舒适性和列车脱轨等分析时不可忽略；同时可激起高频的振动，使轨道和桥梁最大位移响应变小。

(3)车-线-桥耦合有限元分析能直接求得各单元动力响应且不需迭代，综合考虑我国一般线路轨枕间距以及计算精度和效率，轨道单元长度的合适取值范围为0.5～1 m，且列车最小轴距间轨道单元数不应少于2个。

(4)所提轨道-桥梁耦合单元可方便应用于连续梁桥等复杂桥梁，可按较大的桥梁节段长度作为桥梁单元长度，而采用较短的轨道单元，以方便建模和计算。

[1] 夏 禾.车辆与结构动力相互作用[M].北京:科学出版社,2002.

[2] Biggs J M. Introduction to Structural Dynamics[M]. New York: McGraw-Hill, 1964.

[3] Timoshenko S, Young D H, Weaver Jr W. Vibration Problems in Engineering(4th Edition)[M]. New York: Wiley, 1974.

[4] Yang Y B, Yau J D. Vehicle-bridge interaction element for dynamic analysis[J]. Journal of Structural Engineering, 1997, 123(11): 1512-1518.

[5] Yang Y B, Chang C H, Yau J D. An element for analyzing vehicle-bridge systems considering vehicle′s pitching effect[J]. International Journal for Numerical Methods in Engineering, 1999, 46(7): 1031-1047.

[6] Lee Y S, Kim S H, Jung J. Three-dimensional finite element analysis model of high-speed train-track-bridge dynamic interactions[J]. Advances in Structural Engineering, 2005, 8(5): 513-528.

[7] 曾庆元.弹性系统动力学总势能不变值原理[J].华中理工大学学报,2000,28(1):1-3.

[8] 曾庆元,郭向荣.列车桥梁时变系统振动分析理论与应用[M].北京:中国铁道出版社,1999.

[9] Lou P, Zeng Q Y. Formulation of equations of motion of finite element form for vehicle-track-bridge interaction system with two types of vehicle model[J]. International Journal for Numerical Methods in Engineering, 2005, 62(3): 435-474.

[10] 程远胜.列车-轨道-桥梁动力相互作用分析[J].华中科技大学学报(自然科学版),2002,30(1):84-86.

[11] Lou P, Yu Z W, Au F T K. Rail-bridge coupling element of unequal lengths for analysing train-track-bridge interaction systems[J]. Applied Mathematical Modelling, 2012, 36(4): 1395-1414.

[12] Liu X W, Xie J, Wu C. Semi-analytical solution of vehicle-bridge interaction on transient jump of wheel[J]. Engineering Structures, 2008, 30(9): 2401-2412.

[13] 娄 平,曾庆元. 车辆-轨道-桥梁系统竖向运动方程的建立[J].铁道学报,2004,26(5):71-80.

[14] 翟婉明.车辆-轨道耦合动力学(第3版)[M].北京:科学出版社,2007.

[15] Bowe C J, Mullarkey T P. Wheel-rail contact elements incorporating irregularities[J]. Advances in Engineering Softerware, 2005, 36(11-12): 827-837.