基于振动监测的斜拉索时变索力识别方法
2013-01-11张福俭毛晨曦
张福俭, 李 惠, 毛晨曦,2
(1.哈尔滨工业大学 土木工程学院, 黑龙江 哈尔滨 150090; 2.中国地震局工程力学所, 黑龙江 哈尔滨 150080)
斜拉索是斜拉桥上最重要的结构构件之一,索力的往复变化会造成索的疲劳损伤。索力的识别对于斜拉桥的维护与安全评定具有重要的意义,国内外有很多关于索力识别的文献报道。基于振动法的索力识别方法由于其低成本和便捷性,在健康监测实践中广泛采用。
Casas[1]、Hiroshi[2]各自采用不同的索力与基频之间的关系,建立了基于基频的索力识别方法;Ressel和Lardner在他们的索力识别中重点强调了模态阶跃现象[3];Ren[4]、Geier[5]采用了基于模态分析的索力识别方法;Park等[6]、Kim和Park[7]采用了基于灵敏度分析的方法进行了索力识别。Kim等[8]还对上述各种识别方法进行了对比研究,他们建议采用系统辨识方法和张紧弦理论方法。Ceballo和Preto[9]、Ren[10]、Fang和Wang[11]采用曲线拟合的方法建立了两端固支索的索力与基频之间的关系,并基于该关系提出了索力识别的方法。
国内外与此相关的研究还有许多,但是以往振动法一般只能识别在特定时间内的索力的平均值,无法识别时变的索力。因此,所得到的索力识别结果无法用于索的疲劳损伤评估,这是非常遗憾的。本文提出了一种结合扩展卡尔曼滤波和小波级数的时变索力识别方法。
1 理论推导
1.1 斜拉索的运动方程
如图1所示,斜拉索的支座为A、B。B点是固定支座,A点是沿着AB方向(记为ξ方向)的滑动支座。索承受两个方向的外力:垂直索长方向的(如风荷载等)和由车辆引起的索支座移动。如前所述,车辆的通过会引起索力的变化。另外,采用如下假定:(1)斜拉索的自重远小于张力,拉索处于小垂度状态,因此自重和抗弯刚度引起的位移可以忽略,因为它们都是二阶效应[12];(2)由风荷载引起的横向位移独立于由车辆荷载引起的轴向变形。这样η方向的平衡方程如下(受力分析如图2):
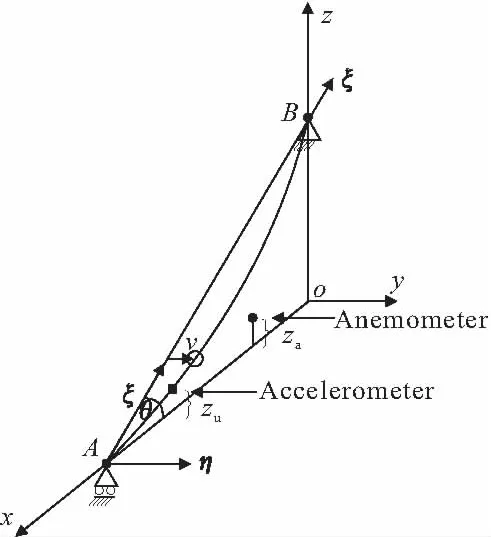
图1 斜拉索模型
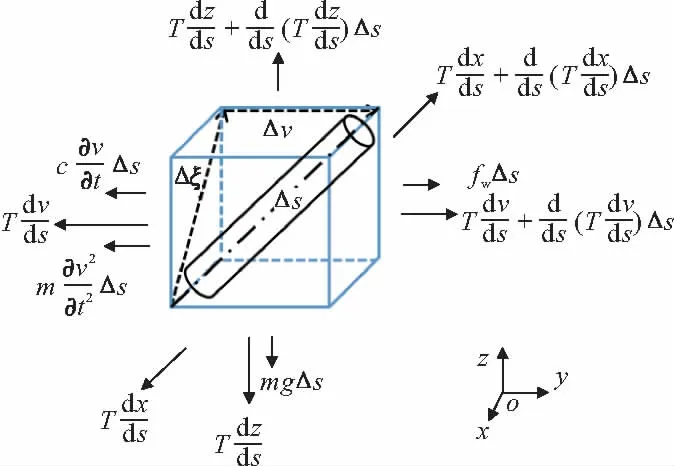
图2 微元体受力分析
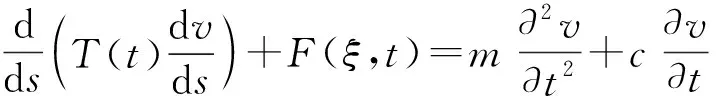
(1)
式中,T(t)是拉索张力,它随着车辆荷载的通过是时变的;F(ξ,t)是垂直于索长方向的外部激励(这里主要考虑横向风荷载);v是沿y方向的横向挠度;m是单位长度质量;c是单位长度阻尼系数;s代表微元长度。
沿ξ方向的微元平衡方程为
(2)
方程(2)可以直接积分得到
(3)
式中H(t)代表索力的水平分量,可认为沿索长不变。将方程(3)带入(1)可得
(4)
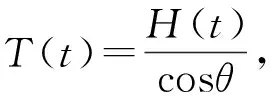
(5)
边界条件:
v(0,t)=0,v(L-u(t),t)=0
(6)
式中,L是索的长度;u(t)代表索端沿ξ方向的运动。.考虑到沿索长方向的索端移动远小于索长,可忽略索的轴向惯性力。边界条件(6)可以简化为
v(0,t)=0,v(L,t)=0
(7)
1.2 索运动方程的近似级数解
索的动挠度可以用有限级数表示为
(8)
式中,qj(t)是第j阶模态坐标;φj(ξ)是满足几何边界条件的连续的形函数,并且φj(0,t)=0,φj(L,t)=0满足正交条件[13]:

(9)
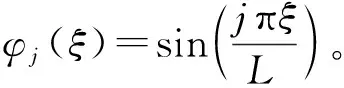
将方程(8)带入(5),可以得到
H(t)qj(t)φj″(ξ)]=F(ξ,t)
(10)
式中,r是待研究的模态阶数。
在方程(10)两侧同时乘以φi(ξ)并沿索长积分即可得到矩阵形式下的模态域振动方程为
(11)
式中,质量矩阵M=[mij]; 阻尼矩阵C=[cij]; 刚度矩阵K=[kij];模态激励Fq=[Fq1Fq2…Fqr]T,各矩阵元素可由如下方程确定:
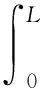
(12)
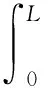
(13)

(14)

(15)
1.3 索力的识别
取任一阶模态的振动方程
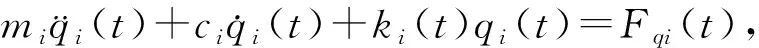
i=1,2,…,r
(16)
其中的时变刚度ki可以用Vj子空间的小波尺度函数表示为
(17)
假定阻尼已知,这样方程(16)可以表示为
AP=Q
(18)
其中
An×(l+1)=
(19)
(20)
(21)
矩阵A可以由小波尺度函数及模态形函数的离散点采样值得到。垂直索力方向的外荷载可以由风速仪测量得到,这样Q也可以得到。由于广义坐标是不能直接测量得到的,它们需要由测量到的位移、速度或加速度变换得到。
如果传感器数目与研究模态的阶数相同,那么广义坐标可以由如下方程得到:
(22)
1.4 由有限观测进行索力识别
通常在索上只能安装有限数量的传感器。因此传感器的数量是小于控制模态的数量的,这时可以采用如下方法确定广义坐标。
当只有有限观测时,如{v(ξ1,t),…,v(ξi,t)}T,而{v(ξi+1,t),…,v(ξr,t)}T没有被观测到。我们采用扩展卡尔曼滤波来根据已观测的部分对未观测的部分进行估计。令v0={v(ξ1,t),…,v(ξi,t),v(ξi+1,t),…,v(ξr,t)}T,则根据公式(22)
q0=Φ-1v0
(23)
将公式(23)带入(11),得到如下在物理坐标下的运动方程:
(24)
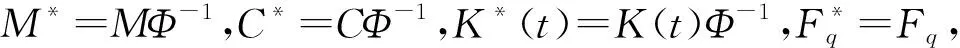
(25)
(26)
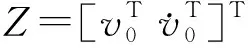
p(v*)~N(0,R)
(27)
式中,R为矩阵v*(t)的协方差矩阵。
将方程(25)和方程(26)变换为离散形式[14]
(28)
(29)
其中
(30)
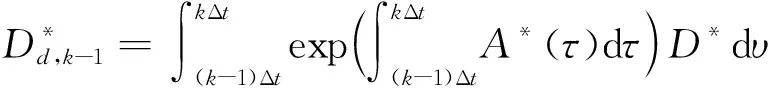
(31)
(32)
式中,Δt是采样周期。
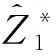
(2)根据过程方程,有对tn+1时的先验估计
(33)
(34)
(3) 计算卡尔曼滤波增益κn+1
(35)
(4)得到状态变量和方差矩阵的最优估计为
(36)
(37)
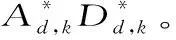

图3 小波-扩展卡尔曼滤波识别数据流程
2 数值试验
研究方法如下:首先,由ANSYS有限元程序对桥梁在车辆荷载下的索力响应进行模拟;然后,根据所得到的时变索力采用Newmark-β法求解方程(11),得到索在环境激励和轴向激励共同作用下的响应;最后,选取部分索上的响应作为观测,进行索力的识别。
2.1 背景资料
本文选取滨州黄河公路大桥上最长的索N26作为研究对象,其基本信息如表1所示。

表1 N26索的基本信息
轴向激励,由ANSYS模拟生成,模拟工况为50 t卡车以20 m/s的速度通过大桥,结果如图4(a)。索的横向荷载采用人工风,模拟风速为20 m/s如图4(b)所示。这样,模态位移、模态速度、模态加速度都可以通过求解方程(11)得到。
(a) 由自重和车载引起的索应力 (b) 人工风时程图4 索的轴向及横向激励
2.2 通过对一个模态所有状态变量观测而得到的索力识别结果
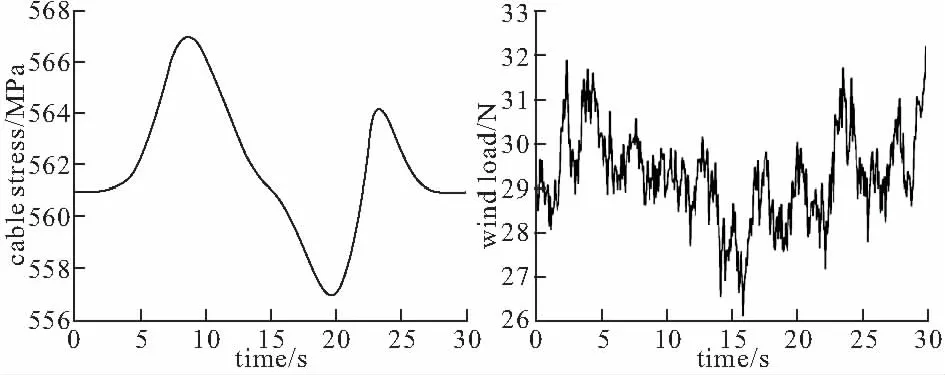
这里采用Db16小波母函数进行索力识别。识别结果(如图5)显示此方法具有很高的精度,但是存在比较明显的边端效应。
(a) 识别到的索力变化系数 (b) 放大的索力变化系数 图5 全观测下索力识别结果
2.3 通过有限观测得到的索力识别结果
沿索长观测所有的位移、速度和加速度是不现实的,因此,这里采用扩展卡尔曼滤波来进行有限观测条件下的索力识别。在下面的识别中,只观测到索上两点的位移。
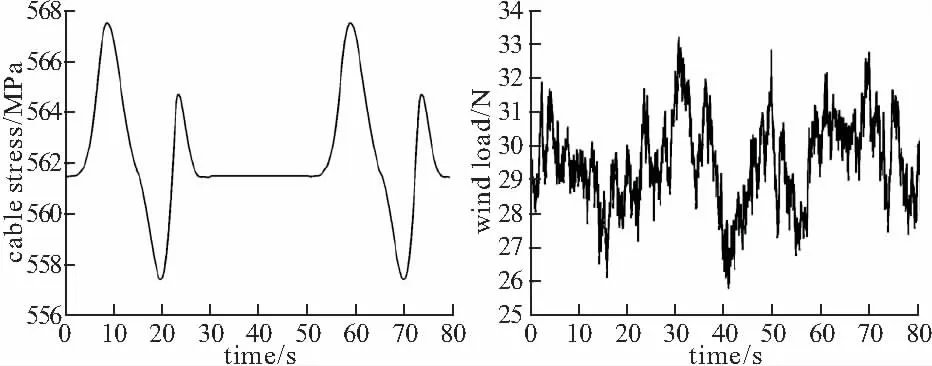
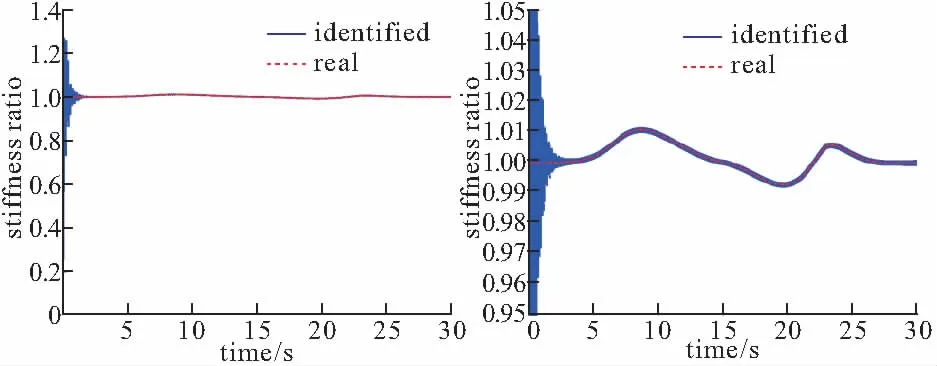
(a) 轴向输入 (b) 横向人工风输入图6 有限观测下工况的轴向和横向输入
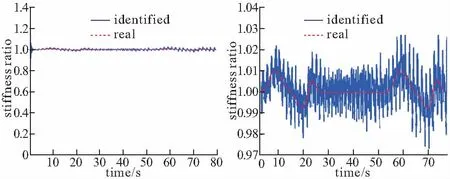
(a) 识别的刚度变化系数 (b) 放大的刚度变化系数图7 有限观测下的刚度变化识别结果
为了验证所提出方法的有效性,这里采用了一个稍微复杂一些的工况:模拟两辆50 t重车先后分别过桥,第一辆车的速度为20 m/s,第二辆车的速度为30 m/s。这样的工况下(图6),识别结果如图7所示。
3 结 论
本文提出了一种基于小波级数结合卡尔曼滤波的时变索力识别方法。以滨州黄河公路大桥为背景,进行了数值模拟研究,结果表明:(1)在观测全局信息时,本文所提出的方法对于较小的索力变化亦有较高的精度;(2)在有限观测条件下本文方法依然可行,但识别结果精度降低。
[1] Casas J R. A combined method for measuring cable forces: the cable-stayed Alamillo bridge, Spain [J]. Structural Engineering International, 1994, 4(4) : 235-240.
[2] Zui H, Shinke T, Namita Y. Practical formulas for estimation of cable tension by vibration method [J]. Journal of Structural Engineering, 1996, 122(6): 651-656.
[3] Russell J C, Lardner T J. Experimental determination of frequencies and tension for elastic cables [J]. Journal of Engineering Mechanics, 1998, 124(10): 1067-1072.
[4] Ren W X, Chen G , Hu W H. Empirical formulas to estimate cable tension by cable fundamental frequency [J]. Structural Engineering and Mechanics, 2005, 20(3): 363-380.
[5] Geier R, De Roeck G , Flesch R. Accurate cable force determination using ambient vibration measurements [J]. Structure and Infrastructure Engineering, 2006, 2(1): 43-52.
[6] Park S, Choi S, Oh S T,et al. Identification of the tensile force in high-tension bars using modal sensitivities [J]. International Journal of Solids and Structures, 2006, 43(10): 3185-3196.
[7] Kim B H,Park T. Estimation of cable tension force using the frequency-based system identification method [J]. Journal of Sound and Vibration, 2007,304(3-5): 660-676.
[8] Kim B H, Park T, Shin H,et al. A comparative study of the tension estimation methods for cable supported bridges [J]. International Journal of Steel Structures, 2007,7(1): 77-84.
[9] Ceballos M A , Prato C A. Determination of the axial force on stay cables accounting for their bending stiffness and rotational end restraints by free vibration tests [J]. Journal of Sound and Vibration, 2008; 317(1-2): 127-141.
[10] Ren W X, Liu H L , Chen G. Determination of cable tensions based on frequency differences [J]. Engineering Computations, 2008, 25(2): 172-189.
[11] Fang Z ,Wang J. Practical formula for cable tension estimation by vibration method [J]. Journal of Bridge Engineering, 2012,17: 161-164.
[12] Irvine H M. Cable Structures [M]. Cambridge : The MIT Press, 1981.
[13] Li R H. Galerkin Finite Element Method for Boundary Value Problems (in Chinese) [M].Beijing: Science Press, 2005.
[14] Franklin G F, Workman M L , Powell D. Digital Control of Dynamic Systems[M]. Boston: Addison-Wesley Longman Publishing Co Inc, 1997.
