相互依存网络鲁棒性研究综述
2013-01-08李国颖成柏松李大庆
李国颖,成柏松,张 鹏,李大庆
(1. 北京邮电大学理学院 北京 海淀区 100876; 2. 北京航空航天大学可靠性与系统工程学院 北京 海淀区 100191)
自从小世界特性[1]和无标度特性[2]被提出以来,国内外掀起一股研究复杂网络的热潮。经过十几年的研究,科学家们形成了一套行之有效的复杂网络理论,这个理论已成为研究复杂系统和复杂性科学的重要工具。复杂网络的研究具有重要的现实意义,社会中的很多实际系统都可以被抽象成复杂网络进行研究。如生态系统[3-4]、交通运输系统[5]、计算机网络系统[6]及经济系统[7-8]等。其中,对关系到国计民生的重要基础设施系统的研究显得尤为重要,通过分析这些网络的鲁棒性,能够揭示系统崩溃的条件及规律,找出预防基础设施系统崩溃的办法,使得社会经济生活更加稳定。
21世纪初,已经有人从工程学的角度,分类、建模、分析了基础设施系统间的相互依存关系,评估这些系统在遭受突发状况或自然灾害时的脆弱性。文献[9]将基础设施系统间的相互依存关系分为四类:物理依存关系、网络依存关系、地理依存关系以及逻辑依存关系。文献[10]指出基础设施系统之间的相互依存关系既是一种契机,也是导致系统脆弱性的关键所在。在基础设施系统建设中,通过分析基础设施系统毁坏的历史案例,结合系统脆弱性的指标,可以针对性地减少不利的相互依存关系。文献[11]调查了2001年世界贸易中心遭受恐怖袭击后造成的持续性影响,认为不同的相互依存关系需要不同的风险管理策略。文献[12]的工作提供了一种管理控制物理依存关系的可操作手段。文献[13]量化了脆弱性和可操作性,据此来评估基础设施系统间相互依存关系。文献[14]根据系统的结构和功能特性,建立相互依存的基础设施系统模型,用以分析系统的脆弱性。文献[15]基于统一建模语言(UML)建立了基础设施系统的参考模型,用以帮助描述和管理基础设施。2010年,相互依存网络的理论分析模型被提出,分析了级联失效过程,开启了人们从复杂网络角度研究相互依存网络的新篇章。
对复杂网络拓扑结构的研究是理解复杂系统性质和功能的重要途径。以往的研究都是单独分析某个网络,如互联网[16]、航空网[17]、社交网[8,18]等。随着科学技术的日益发展,系统之间的依赖会越来越强。为此,需要将研究目光由单个网络构成的系统转向更一般的有相互作用的多个网络所组成的系统,进而对实际系统的运作有更深入全面的了解。相互依存网就是基于此背景提出的。相互依存网(interdependence networks)就是具有相互作用关系的两个或多个网络所组成的一个网络系统[19],示意图如图1所示。
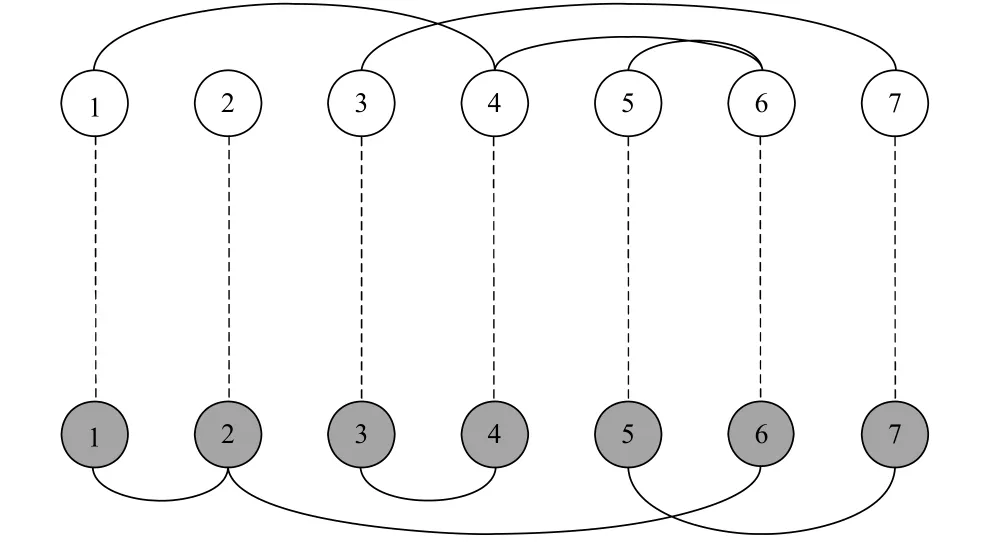
图1 相互依存网络示意图
图1中,白色节点和黑色节点分别代表两个不同网络中的节点,实线代表网络内部的连接关系,虚线代表网络间的依存关系,这就构成了一个相互依存网。实际生活中存在很多这样的相互依存网,如电力-计算机网[19],电站间互相传输电力,计算机之间互相传输信息,电站间进行电力传输需要计算机进行控制,而计算机之间互相通讯又依赖于电站供给必需的电力。近几年来,相互依存网的研究已逐渐成为国内外的一个热点话题。就目前的了解而言,关于相互依存网的研究主要集中在相互依存网的鲁棒性方面。本文将从以下四个方面分别介绍相互依存网的鲁棒性研究:一对一连接关系的相互依存网的鲁棒性;多对多连接关系的相互依存网的鲁棒性;多个网络组成的网络系统的鲁棒性;无标度网络构成的相互依存网的鲁棒性。
1 双层相互依存网的鲁棒性研究
现代社会中,为社会生产和居民生活提供公共服务的基础设施系统,包括交通、通讯、水电、能源等系统之间的关系越来越紧密,对某个基础设施系统的破坏会给人们的生产生活带来极大的损失,所以研究并量化这些基础设施系统网络的鲁棒性显得尤为重要。网络的鲁棒性是指在移走部分节点后网络中的绝大部分节点仍是连通的,那么就称该网络对节点故障具有鲁棒性[20]。以往的研究中,采用了两种方法来模拟实际系统的故障模式,一种是随机故障模式,即随机地移除网络中的节点;二是蓄意攻击模式,比如移除那些网络中度较高或者介数较高的节点。研究表明,随机网络对随机故障具有脆弱性,对蓄意攻击具有很高的鲁棒性,而无标度网络对随机故障具有高度的鲁棒性,对蓄意攻击又具有脆弱性[20]。
在很多实际网络中,一个或几个节点的故障,会通过节点之间的耦合关系引发其他节点的故障,产生连锁反应,最终导致相当一部分节点故障甚至是整个网络的崩溃,这就是级联失效的过程。
衡量网络的鲁棒性一般有两个参量:级联失效过程中的最大连通子团大小以及渗流阈值。第一个参量的值越大,则网络的鲁棒性就越好,这是比较直观的。在网络级联失效过程中,网络整体的连通性会随之改变,当故障节点达到一定比例时,网络完全破碎,发生由完全连通态(有序)到完全分裂态(无序)的一个非连续或者连续的相变过程。此时的故障节点比例阈值就是渗流阈值,这个参量间接地反映了网络的鲁棒性。通过以往的研究发现,在单层网络中,网络的级联失效呈现出渗流中的连续的二级相变的现象,这很类似于水在发生气液相变时的临界现象。然而,在相互依存网络中,由于两个网络之间存在相互依存关系,网络的级联失效表现为一级相变,这时存在一个渗流阈值,渗流阈值越小,网络的鲁棒性越高。最近,一些研究致力于建模分析相互依存网络的级联失效过程[10-15,21-22]。然而,这些工作都没能给出一个系统的理论模型。
1.1 一对一连接关系的相互依存网的鲁棒性
文献[19]在2010年提出一个相互依存网的理论分析模型,描述了具有双向依赖关系的网络特征。这个模型考虑了两个有相同节点个数的网络A和B,A网络上的节点Ai与B网络上的节点Bi存在相互依存关系,如果节点Ai失效,则节点Bi也会失效。同样地,如果节点Bi失效也会引起节点Ai失效。该模型假定只有属于网络A或网络B的最大连通子团中的节点能够保持功能,而属于其他子团的节点会失去功能。该模型的级联失效过程如图2所示,假设A网络中的一个节点失效并被移除(如图2a),则A网络中所有与其相连的边均失效且移除,这时网络A分裂为3个子团a11、a12和a13(如图2b),不属于A网络的最大连通子团的节点也失效;A网络中的失效节点也会导致B网络中相应的节点失效,从而导致B网络分裂成4个子团b21、b22、b23、b24(如图2c所示),不属于B网络最大连通子团的节点也因此失效;再进一步,B网络的失效节点也会导致A网络中相应的节点失效,如此进行下去,最终达到稳定状态(如图2d所示)。文章表明当移除节点比例达到一个临界值(1-pc)时,会导致整个相互依存网络崩溃。

图2 级联失效过程模型[19]
上述文章还发现,相互依存网中的级联失效过程表现为一级相变,而以往研究单层网络的级联失效过程为二级相变,说明相互依存网络比单层网络更脆弱。如:2003年8月14日,美国东北部、中西部和加拿大东部联合电网发生震惊世界的大停电事故,就是因为电力网跟计算机网之间的级联失效导致的。这一案例提醒我们必须增强现实中相互依存的关键基础设施系统网络的鲁棒性,这些系统的崩溃会给人们带来巨大损失。这个问题近几年已开始被着手研究。文献[23]通过减小相互依存网络间的耦合强度,即减少整个系统中具有相互依存关系的节点比例,使渗流相变由一级相变转变为二级相变,从而提高了网络的鲁棒性。
文献[19]是基于相互依存网络之间的连接关系是一对一随机连接这个假设提出的,但是现实中也存在其他情况。如,考虑电力-计算网模型,电站依靠计算机网进行调控,而计算机网需要电站提供电力支持。这时,合理的情况是中央通讯节点依赖于一个中央电站而非一个小电站提供电力支持。另外全球航空网络和全球港口网络中流量大的港口和航空站之间也更倾向于相互作用。通过以上例子我们发现,实际相互依存网中,网络间的依存关系存在一定的度度相关性和局部相似性。文献[24]基于这个考量,定义了相互依存网络的网间相似性(inter-similarity),并提出两种高网间相似性的相互依存网构建方法,一是将两个网络中度值大的节点建立依存关系,另一种是将两个网络中聚类系数大的节点建立依存关系,得出通过增加网络间的相似性,能显著增强相互依存网络对随机攻击的鲁棒性的结论。之后,文献[25]构造了一个相关耦合网络(correspondently coupled networks, CCNs)模型,在两个具有相同度分布的网络中,将两个度值相等的节点建立依存关系。同时,为了与相关耦合网络作对比,作者还建立了一个随机耦合网络(randomly coupled networks,RCNs),但并非是将度值相等的节点建立依存关系,而是不用考虑两个节点的度值,随机地建立依存关系。他们发现,相关耦合网络的渗流临界阈值pc小于随机耦合网络的临界阈值。也就是说,在相同度分布情况下,相关耦合网络的鲁棒性更高。并且他们还指出,网络度分布越宽,相关耦合网络的鲁棒性将越高。
1.2 多对多连接关系的相互依存网的鲁棒性
上述工作有一个基础假设,即网络间节点的连接关系是一对一连接的,然而实际系统中也存在着多重对应连接。文献[26]用数值解析的方法分析了有多重依存关系的耦合网络的级联失效过程。假设网络中的一个节点与另一个网络中的多个节点有依存关系,并且只要它的依存节点中有一个正常工作,它就能正常工作。如图3所示,网络A中的节点A2跟网络B中节点B2和B3有依赖关系,只要B2和B3其中一个工作,则节点A2仍继续工作。这种多重依存关系导致了级联失效由一级相变转化为二级相变,网络鲁棒性得到明显增强。
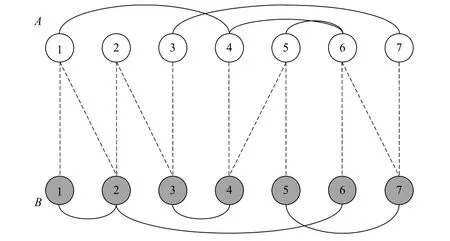
图3 具有多重依存关系的相互依存网示意图
其他的文献考虑了定向攻击和部分耦合,这两个因素都会对相互依存网络的鲁棒性有影响。对网络的定向攻击和随机攻击唯一的不同在于初始攻击节点的选择,文献[27]给出将定向攻击等效为随机攻击的方法,并给出了解析证明。文献[23]考虑了相互依存网络中部分耦合时的鲁棒性问题,发现通过减少两个网络之间的耦合强度,能显著提高相互依存网络的鲁棒性。文献[28]综合考虑了上述两种情况,提出一个一般化的理论模型,这为高鲁棒性网络的设计提供了参考。
另外,文献[29]发现,通过在网络中选择合适比例的自治节点,能有效地避免相互依存网的级联失效。所谓自治节点,就是网络中那些不依赖于其他节点的失效而失效的节点。作者选择每个网络中度或者介数较高的部分节点为自治节点,这样得到的网络具有较高的鲁棒性。此种方法应用在意大利电网与通讯网间时发现,只要有意地保护4个最高介数的通讯服务器,可以显著提高网络鲁棒性,减小网络崩溃的可能。
1.3 无标度网络构成的相互依存网的鲁棒性
在前文的陈述中,主要依据网络之间的连接关系以及相互依存的网络个数来对现有工作归类整理。由于随机网络和随机规则网络能够利用生成函数得到精确的解析解,大多数工作都选用这两种网络模型进行研究,但不能因此忽视无标度网络研究的重要性。上述文章中提到的很多实际网络都近似呈现幂率分布,如:英特网,航空网,社交网以及科学家合作网[2,30-31]等。为了能够很好的突出无标度网络研究的重要性,特意将相互依存网已有工作中涉及幂率分布的部分重点列出来,希望对接下来的科研工作或者实际应用有所借鉴和指导。
文章[19]中通过分析相互依赖的无标度网络发现,随着网络度分布越宽,渗流阈值pc越大,这说明度分布较宽的网络的鲁棒性更高。这种趋势跟单层网络中的结论(对于随机攻击,无标度网络的鲁棒性要显著高于随机网络)不同,这是因为,在相互依赖的无标度网络中,一个网络中度大的节点可能会依赖于另一个网络中度很小的节点,这样的话,度小的节点失效可能会导致另外一个网络中度大的节点失效,继而引发该网络大面积的失效,之后又会影响第一个网络中的多个节点失效,最终导致整体网络崩溃。文献[25]中的分析证明很好地验证了上述说法,即当相互依存节点的度分布相同时,如果网络的度分布越宽,网络的鲁棒性就越高,这跟单层无标度网络的鲁棒性结论一致。类似地,文献[24]也说明通过增加网络间的相似性,能显著增强相互依存网络对随机攻击的鲁棒性。另外,文献[25]还提到,对于相互依存的无标度网络,当度分布存在有限二阶矩时,渗流相变呈现出一级相变的现象。参照文献[25]的结论,可以认为如果相互依存节点的度分布不相关,那么渗流相变都会表现为一级相变[19,23-24]。这说明研究在依赖性和连通性方面具有相关性的相互依存网络是很有必要的。
2 多个网络组成的相互依存网络系统的鲁棒性研究
以上讨论都是基于两个系统构成的相互依存网络,没有考虑多种设施之间的相互依赖,如水和食物供应网络、通讯网、燃油网、金融交易网或电网等[32-33],为了更好地把握和理解这种系统的鲁棒性,最近的研究开始关注多层网络系统。文献[34]提出了一个研究n层网络渗流问题的理论分析模型。
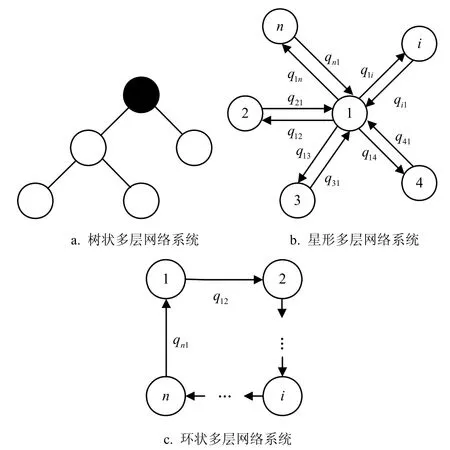
图4 多层网络系统示意图[34]
如上图4所示,每个节点(圆圈)代表一个网络,节点间的边表示网络间存在依存关系。这种n层网络构成的系统也可表示为多层网络系统(network of networks, NON)。当n=1时,系统为单层网络,相应的渗流相变为二级相变;当n>1时,系统发生级联失效,并且相变转化为一级相变。这个结论说明,数学和物理中的经典渗流理论只是多层网络系统渗流理论在n=1时的特殊情况。同时作者还给出了3种不同拓扑结构的多层网络系统,并得到了各自相应的解析结果。需要说明的是,对于前两种情形,网络间的依赖关系是一对一双向无反馈的,而最后一种情形是单向的。
1) 树状多层网络系统。作者给出了在级联失效结束后,网络中存在最大互连子团的概率为:
该式也适用于星形(如图4b所示)和线形拓扑结构[35]。由式(1)可得到,随着n的增大或k的减小,临界渗流阈值pc也会增大。并且,当系统中网络个数n固定时,若k 2) 星形多层网络系统。若移除位于系统中心的网络(如图4b中的网络1)中的部分节点,失效就会传播到系统中其他所有的网络,然后再反馈到中心网络,如此循环往复。进一步的研究说明,式(1)中的P∞还与多层网络系统的拓扑结构有关。 3) 环状多层网络系统。假设系统中每个网络的平均度相同,每个网络都移除相同比例(1−p)的节点,研究得到: 式中,q为环状多层网络系统中(如图4c所示)第i+1个网络依赖于第i个网络的节点比例。当q=1时,代入式(2)得P∞= 0 ,当q=0时,将会得到单层网络的最大连通子图大小的形式。作者又给出了介于0和1之间的两个不同q值的数值模拟结果。综合式(1)和式(2)可以看出,树状多层网络系统的鲁棒性跟网络个数n有关,而环状多层网络系统与网络个数n无关。 本文对近两、三年来关于相互依存网鲁棒性的研究进行了较为全面的归纳总结。在相互依存网中,节点的失效会传播到有相互依存关系的各个网络,导致整个网络系统的级联失效。文献[19]提出的分析模型使得能够很好地追踪级联失效的物理过程,并导出最终稳定态的解。对于相互依存的基础设施系统网络,找到能显著提高其鲁棒性的方法是至关重要的。目前为止,提高相互依存网络的鲁棒性有三种基本方法:1) 增加网络中自治节点的比例[23],选择度较高的节点作为自治节点[29];2) 建立相互依赖关系使节点间具有相似性[24-25];3) 保护那些度高的节点免受攻击[29]。希望以后能有更多有效的提高网络鲁棒性的方法出现,用以保证实际生活中重要的基础设施系统的稳定,维持社会的安全稳定。相互依存网出现在实际生活的方方面面,如:包括铁路网、航空网以及其他交通网的交通系统[24,37]。在生理学领域,人体也可看作由心血管系统、呼吸系统、大脑神经元系统以及神经系统组成的相互依存网络系统,它们之间的相互作用为人类活动提供了基本的保障。在生物学领域,不同蛋白质的功能取决于与其他蛋白质的相互作用,这可看作是一种相互依存网络,多种不同功能的蛋白质之间构成的网络,可以被认为是一个相互依存网络系统。在经济学领域中,银行、保险公司以及商业公司之间也是一种相互依存的关系。然而,迄今为止,只有少量实际相互依存系统用渗流理论进行实证研究分析[24,37-39],而且研究相互依存网的理论模型依然具有局限性。在将来的研究中,应该把目光集中在对更多的实际相互依存网的建模分析上,并且在此过程中不断完善理论模型,使之能更好地揭示现实系统的本质属性。另外,网络的动力学行为研究也是我们要关注的,包括网络演化模型、演化网络博弈和网络上的信息传播等都属于动力学研究范畴。近几年来,在复杂网络上的传染病、谣言以及计算机病毒等的传播研究已经取得丰富的成果,这为人类的健康和社会的安全稳定做出极大贡献。但在网络间相互作用关系日益增强的今天,单层网络上的动力学研究存在一定局限性,为了更好地反映实际网络的演化行为机制,将这些动力学行为放在相互依存网络中研究就显得尤为重要。除此之外,可以将负载考虑到相互依存网的级联失效过程中,研究负载对级联失效的影响。再者,深入挖掘网络结构的信息,探究导致级联失效的关键性结构,从而更好地保护那些相互依赖的实际系统,这将是未来的研究重点。最后,相互依存网络的地理位置属性在前面的研究中并未提及,而这个因素会对网络结构产生一定影响,希望能在今后的研究中有所涉及。 [1] WATTS D J, STROGATZ S H. Collective dynamics of small world networks[J]. Nature, 1998(393): 440-442. [2] BARABÁSI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999(286): 509-512. [3] ALON U. Biological networks: The tinkerer as an engineer[J]. Science, 2003(301): 1866-1867. [4] KHANIN R, WIT E. How scale-free are biological networks[J]. J Comput Biol, 2006, 13(3): 810-818. [5] GAO Z Y, ZHAO X M, HUANG H J, et al. Research on problems related to complex networks and urban traffic systems[J]. J Tran Sys Eng & Info Tech, 2006,6(3): 41-47. [6] FALOUTSOS M, FALOUTSOS P, FALOUTSOS C. On power-law relationships of the internet topology[J]. Comput Commun Rev, 2000(29): 378-382. [7] BONANNO G, CALDARELLI G, LILLO F, et al. Topology of correlation-based minimal spanning trees in real and model markets[J]. Phys Rev E, 2003(68): 046130. [8] JACKSON M O, ROGERS B W. Meeting strangers and friends of friends: How random are social networks?[J]. Am Econom Rev, 2007(97): 890-915. [9] RINALDI S, PEERENBOOM J, KELLY T. Identifying,understanding, and analyzing critical infrastructure interdependencies[J]. IEEE Control Syst Magn, 2001(21):11-25. [10] ZIMMERMAN R. Decision-making and the vulnerability of interdependent critical infrastructure[J]. 2004 IEEE Int Conf Syst Man Cybern, 2005(5): 4059-4063. [11] MENDONCA D, LEE II E E, WALLACE W A. Impacts of the 2001 world trade center attack on new york city critical infrastructures [J]. J Infrast Syst, 2006(12): 260-270. [12] ROBERT B, MORABITO L, CHRISTIE R D. The operational tools for managing physical interdependencies among critical infrastructures[J]. Int J Crit Infrastruct,2008(4): 353-367. [13] REED D A, KAPUR K C, CHRISTIE R D. Methodology for assessing the resilience of networked infrastructure[J].IEEE Syst J, 2009(3): 174-180. [14] JOHANSSON J, HASSEL H. An approach for modelling interdependent infrastructures in the context of vulnerability analysis[J]. Reliab Eng Syst Saf, 2010(95):1335-1344. [15] BAGHERI E, GHORBANI A A. UML-CI: A reference model for profiling critical infrastructure systems[J].Inform Syst Front, 2009(12): 115-139. [16] WEST B J, GRIGOLINI P. Complex webs: anticipating the improbable[M]. English: Cambridge University Press,2011. [17] BARABÁSI A L, BONABEAU E. Scale-free networks[J].Scientific American, 2003(288): 50-59. [18] BORGATTI S P, MEHRA A, BRASS D, et al, Network analysis in the social sciences[J]. Science, 2009(323):892-895. [19] BULDYREV S V, PARSHANI R, STANLEY H E, et al.Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010(464):1025-1028. [20] 汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006.WANG Xiao-fan, LI Xiang, CHEN Guan-rong. Complex network theory and applications[M]. Beijing:Tsinghua University Press, 2006. [21] JOOST R S. Inoperability input_output modeling of disruptions to interdependent economic systems[J]. Syst Eng, 2006(9): 20-34. [22] MANSSON D, THOTTAPPILLIL R, BACKSTROM M, et al. Methodology for classifying facilities with respect to intentional EMI[J]. IEEE Transactions on Electromagnetic Compatibility, 2009(95): 46-52. [23] PARSHANI R, BULDYREV S V, HAVLIN S.Interdependent networks: reducing the coupling strength leads to a change from a first to second order percolation transition[J]. Phys Rev Lett, 2010(105): 048701. [24] PARSHANI R, ROZENBLAT C. Inter-similarity between coupled networks [J]. Europhys Lett, 2010(92): 68002-68006. [25] BULDYREV S V, SHERE N W, CWILICH G A.Interdependent networks with identical degrees of mutually dependent nodes[J]. Phys Rev E, 2011(83): 016112. [26] SHAO J, BULDYREV S V, HAVLIN S, et al, Cascade of failures in coupled network systems with multiple supportdependence relations[J]. Phys Rev E, 2011(83): 036116. [27] HUANG X Q, GAO J X, BULDYREV S V, et al,Robustness of interdependent networks under targeted attack[J]. Phys Rev E, 2011(83): 065101. [28] DONG G G, GAO J X, TIAN L X, et al, Percolation of partially interdependent networks under targeted attack[DB/OL]. (2011-08-30). http://arxiv.org/abs/1108.5788. [29] SCHNEIDER C M, ARAÚJO N A M, HAVLIN S, et al,Towards designing robust coupled networks[DB/OL].(2011-06-16). http://arxiv.org/abs/1106.3234. [30] ALBERT R, BARABÁSI A L, Statistical mechanics of complex networks[J]. Rev Mod Phys, 2002(74): 47-97. [31] COLIZZA V, BARRAT A, BARTHELEMY M et al.Prediction and predictability of global epidemics: The role of the airline transportation network[J]. PNAS USA,2006(103): 2015-2020. [32] PEERENBOOM J, FISCHER R, WHITFIELD R.Recovering from disruptions of interdependent critical infrastructures[C]//presented at the CRIS/DRM/IIT/NSF Workshop on Mitigating the Vulnerability of Critical Infrastructures to Catastrophic Failures. Washington D C:[s.n.], 2001. [33] RINALDI S, PEERENBOOM J, KELLY T. Identifying,understanding, and analyzing critical infrastructure interdependencies[J]. IEEE Contr Syst Mag, 2001(21):11-25. [34] GAO J, BULDYREV S V, HAVLIN S, et al. Robustness of a network of networks[J]. Phys Rev Lett, 2011(107):195701. [35] GAO J X, BULDYREV S V, HAVLIN S, et al. Robustness of a tree-like network of interdependent networks [DB/OL].(2011-08-30). http://arxiv.org/abs/1108.5515. [36] UM J, MINNHAGEN P, KIM B J. Synchronization in interdependent networks[J]. Chaos, 2011(21): 025106. [37] GU C G, ZOU S R, XU X L, et al. Onset of cooperation between layered networks[J]. Phys Rev E, 2011(84):026101. [38] YA G O, QIAN D J, ZHANG J S, et al. Optimal allocation of interconnecting links in cyber-physical systems:Interdependence, cascading failures and robustness[DB/OL]. (2011-03-04). http://www.ece.umd.edu/~oyagan/Journals/Interdependent_Journal.pdf. [39] GAO J X,BULDYREV S V, STANLY H E, et al. Networks formed from interdependent networks[J]. Nature physics,2012(8): 40-48.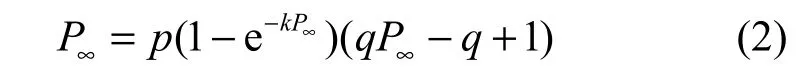
3 总结与展望
