基于排队论的销售模型分析

潘全如

(江苏科技大学数理学院,江苏镇江212003)

0 引言

顾客到达企业寻求服务可以构成一个排队系统[1]。顾客到达过程即为输入过程,企业为服务机构,企业根据需要设置排队规则[2]。顾客到达系统时总是希望等待服务的队列长度越短越好,否则他们在系统中逗留成本比较高,这需要企业在销售时提供相对较高的服务速度,但是如果服务速度增高又会导致服务成本升高。如何在服务台的服务成本与顾客在系统中的逗留成本之间平衡,使两者之和(称为系统的综合成本[3])最小,是一项重要的课题。

1 顾客到达时排队方式的探讨

顾客到达系统的排队方式主要有3种[4],分别如图1所示。

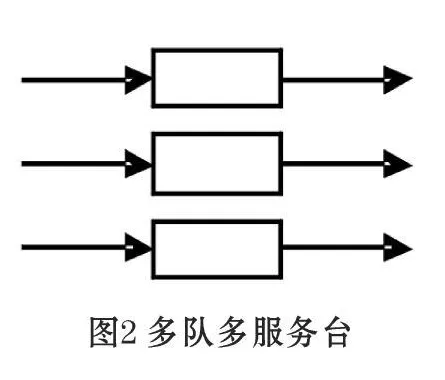
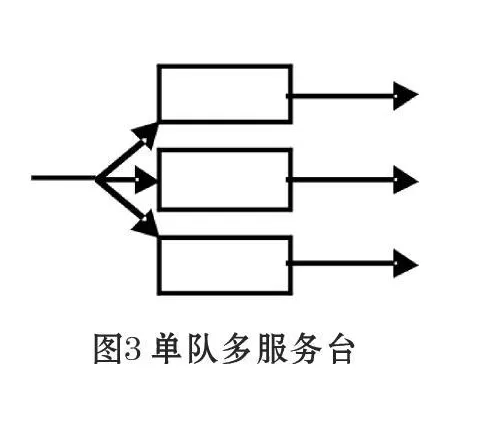
图1为单队单服务台系统,排队等待服务的通道只有一条。图2为多队多服务台系统,每个通道各排一个队,且每个通道只为自己通道上的顾客服务,顾客不能任意插队。图3为单队多服务台系统,即顾客排成一个队,队列中第一个顾客视哪个通道有空就去哪一个通道接受服务。在这里假设顾客到达为泊松到达,企业按先到先服务的规则服务,服务时间服从负指数分布,则上述3个图形就分别对应着 M/M/1系统、n个并联的M/M/1系统、M/M/n系统,其中M/M/1系统是n个并联的M/M/1系统及 M/M/n系统的特殊情况。

企业总是希望系统总是处于非空闲状态的,因为空闲概率越大意味着系统的利用率越低;顾客则希望在系统中的逗留时间越短越好。下面从系统的空闲概率与逗留时间两个角度分析 n个并联的M/M/1系统及 M/M/n系统。由文献[5]知:M/M/n系统的空闲概率为记为pn0;n个并联的M/M/1系统的空闲概率为1-ρ,记为 p00。事实上所以 pn0=,即M/M/n系统的空闲概率小于n个并联的M/M/1系统的空闲概率。由文献[5]知:M/M/n系统的平均等待时间为个并联的M/M/1系统的平均等待时间为

2 销售企业服务方式的探讨

2.1 窗口之间相互帮助的模型分析

对于M/M/1系统,顾客泊松到达,到达强度为λ,服务台的服务时间是平均服务率为 μ的负指数分布,记,当ρ1＜1时,系统有平稳分布,且顾客在系统内平均逗留时间

对于M/M/n系统,顾客泊松到达,到达强度为 λ,每个服务台的服务时间是平均服务率为 μ的负指数分布,整个系统的平均服务率为 nμ,记当ρ2＜1时,系统有平稳分布,且顾客在系统内平均逗留时间;其中

若窗口间相互帮助,则M/M/n系统就相当于如下的M/M/1系统:

例1 n=4,λ=5,μ=2,比较各窗口独立工作与相互帮助时F的大小

显然,无论窗口是否独立工作,¯μ均为nμ,而各窗口相互帮助时顾客在系统中的逗留时间要小于各窗口独立工作时的逗留时间,因而F在各窗口相互帮助时较小,导致这一结果的原因:各个窗口相互帮助时,避免了一些服务人员的闲置。

2.2 同时为k个顾客服务的模型分析

对于有些类型的服务,服务员需要花相当多的时间在来去的路上,如柜台每接一笔订单就向仓库请求发货。如果发货请求时间间隔不大,仓库可将几个请求的货物一起运过来,这样比每接一个请求即发一次货的成本要低。设订单到达服从泊松分布,时刻t系统中订单数为i(i=0,1,…,s)时,订单的到达率为 λi;系统服务时间服从指数分布,每次服务k(k为正整数)个订单,服务率为μ。则可写出状态方程组如下:

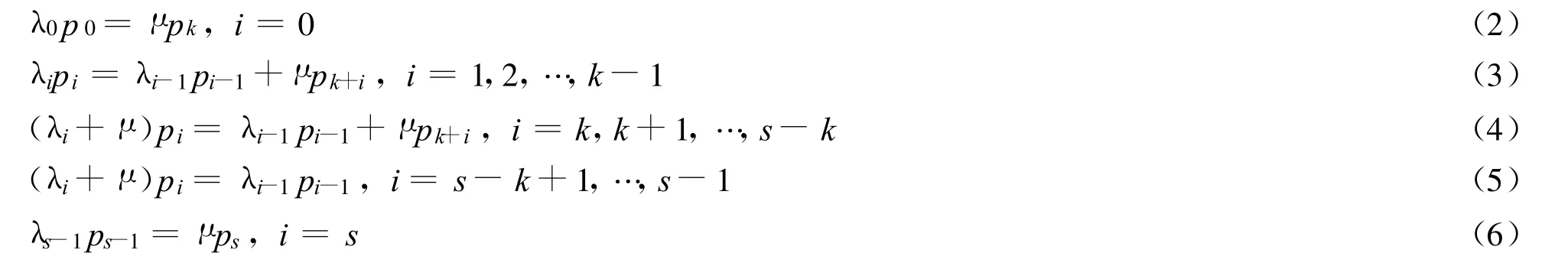
例2 λi=比较每次同时为2个顾客服务与每次只服务一个顾客时F大小,其中a=b=1,且每次同时服务2个顾客时 μ=10,每次只服务一个顾客时 μ=12。

解 (ⅰ)每次只服务一个顾客时,系统就是一个 M/M/1/s系统,此时容易计算出:p0=0.267,p1=0.267,p2=0.20,p3=0.133,p4=0.083,p5=0.05,系统的平均等待队长,系统的平均输入率,顾客在系统中的平均逗留时间0.190=12.190

(ⅱ)每次同时服务2个顾客,将上述数据代入(2)～(6)式及可得:p0=0.184,p1=0.381,p2=0.22,p3=0.123,p4=0.054,p5=0.039,系统的平均等待队长系统的平均输入率,顾客在系统中的平均逗留时间10.588

显然,每次同时服务2个顾客时F较小,导致这一结果的原因:虽然每次同时为两个顾客服务时,顾客在系统中逗留成本有所增加,但此时服务成本下降,且下降的幅度更大。

2.3 服务率可变的排队模型分析

如果队列较长时以较低的速度服务会导致顾客的逗留成本较高,而队列较短时以较高的速度服务会导致服务成本较高。销售企业如果根据排队等待服务的队列长度,适时地调整服务速度,也能够使综合成本降低。设顾客泊松到达,按先到先服务的规则,服务时间服从指数分布,系统中有 i个顾客时到达率为λi,服务率为 μi。令则系统的状态方程如下:

例3 λi=i=0,1,…,6,n=6,a=b=1,比较服务率为 μi=2+0.3i及 μi≡3.2时F的大小。

解:(ⅰ)μi=2+0.3i,此时服务率可变,将上述数据代入(11)式可得:

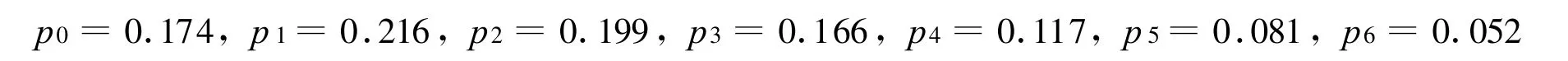
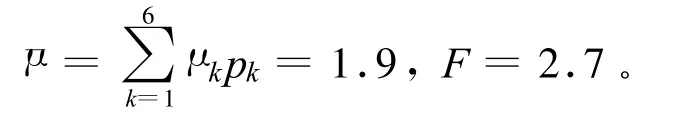
显然,服务率可变时的F较小,即服务速度的适当调整能够降低系统的综合成本。

2.4 有k个顾客类时的模型分析

在上面的讨论中,假定到达的顾客总是同一类型,即所有的顾客在系统中停留单位时间的成本一样,实际情况往往不是这样。现设有k类顾客[8],他们到达系统是以参数为 λk的泊松分布,在系统中逗留单位时间的成本分别为bk,系统对每类顾客的服务时间均服从指数分布,且参数为,系统有s个服务台,且平均服务时间越短的顾客获得服务的优先权[9]越高。则第k类顾客在系统中的逗留时间分别为其中为系统中的顾客数。

例4 设有两类顾客,第一类顾客获得服务的优先权高于第二类。第一类顾客到达率为λ1=10人/小时,第二类顾客到达率为λ2=20人/小时。系统有5个服务台,对两类顾客的服务时间均服从均值为8分钟的指数分布,计算系统在设置优先级时F的值,并与不设优先级时的F比较大小。

解 (ⅰ)设置优先级时,s=5,λ1=10人/小时,λ2=20人/小时,μ=7.5人/小时,所以所以所以在系统设置优先级时顾客在系统中的平均等待时间为=4.4分钟。

(ⅱ)系统没有设置优先级时,此时模型即为 M/M/s系统,其中 s=5,λ=30人/小时,μ=7.5人/小时,

2.5 雇佣帮手的模型分析

是否雇用帮手主要取决于帮手创造的价值是否大于他获得的工资,如果大于则毫不犹豫地选择雇用。

例5 某电子仪器厂员工每人每小时工资为8元,他为公司创造的价值是每人每小时12元。现需要抽调部分员工对售出产品作回访,且认为做回访工作时员工不创造价值,平均每小时需要10名人员来做一次回访工作。现抽调一名员工专门做回访工作,平均4分钟就能完成一次回访,如果给该员工雇用一名帮手,则他平均每3分钟就能完成一次回访,问雇用者的工资不应当超过多少?

解 在本问题中,员工的工资可以当作系统的服务成本,员工因做回访工作时没有创造价值而对公司造成的损失可以看作等待成本,或称为延迟成本。公司的目标是将每小时的服务成本和延迟成本之和最小化。由上述分析可知:预期成本/小时=服务成本/小时+预期延迟成本/小时。服务成本/小时=工资/小时;预期延迟成本/小时=(预期延迟成本/员工)*(预期的员工数/小时),记预期的员工数/小时=λ人/小时,由题意知λ=10人/小时。预期延迟成本/员工=12元*员工做回访工作时花在系统中的小时数=12,记员工做回访工作时花在系统中的小时数=。故延迟成本/小时=12λ.(ⅰ)没有帮手时,因为平均每4分钟完成一次回访,所以μ=15人/小时,小时,服务成本/小时=8元,预期延迟成本/小时=元,此时预期成本/小时=8+24=32元。

(ⅱ)雇用帮手时,因为平均每3分钟完成一次回访μ=20人/小时,小时,设 x为雇用人员的工资,则服务成本/小时=(8+x)元/小时,预期成本/小时=小时=12元/小时,于是雇用帮手时的预期成本/小时=(8+x+12)元/小时=(20+x)元/小时。

由题意知:雇用帮手时的预期成本应≤没有帮手时的预期成本,即20+x≤32,即 x≤12时,系统应当雇用帮手。

3 库存容量对综合成本的影响

保持适量的库存[11]对综合成本有着重要的影响:库存少了会影响销售;库存多了会影响资金流通,且保管费用也高。那么保持怎样的库存才是合理的呢?

假设 (ⅰ)顾客订货时刻是一个泊松过程,需定货 i个单位的顾客到达率为λi,i=1,2,…,m,记 λ=原始库存为也是最大库存量。顾客订货时只要有库存就立即发货;若缺货就让顾客等待,且等待需求总数不超过N个单位,否则拒绝其进入系统。顾客发生i个单位需求时,系统立刻发出i个单位的订货,以补充库存;(ⅲ)系统的服务时间服从指数分布,但服务率与尚未交付的订货总数有关,系统中有i个单位尚未交付时服务率就为μi;(ⅳ)每个单位的需求缺货单位时间的损失称为第一类缺货损失[12],记为C1(C1＞0);每发生一个单位的缺货所造成的损失费称为第二类损失缺货费,记为C2(C2＞0);仓库中每个单位的存货存放单位时间的保管费用记为C3(C3＞0);仓库存放存货的每个单位空间在单位时间内所需修建维护费记为C4(C4＞0)。

设ξ(t)为时刻t尚未交付的订货总数。因为系统允许排队长度有限,故系统的平稳概率存在,设为 pn,n=1,2,…,N。根据以上假设,写出系统的状态方程组如下:

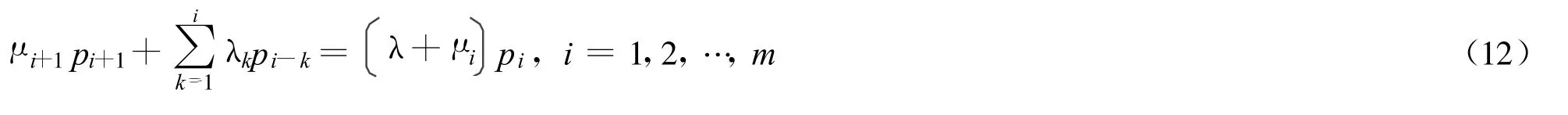
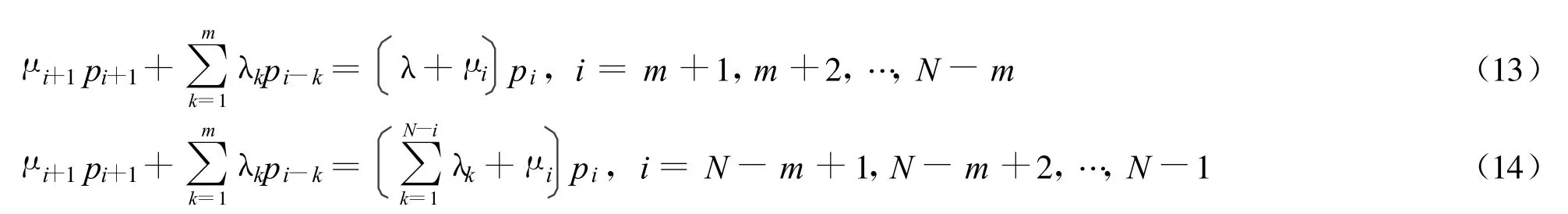
设c(s)为单位时间内的平均总费用,则

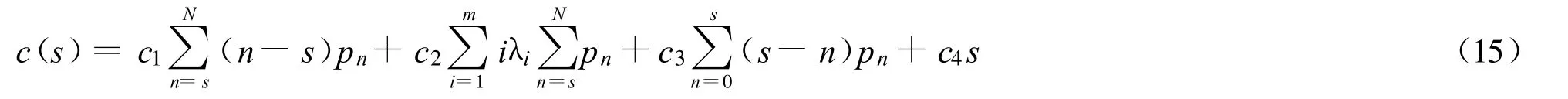
下面求c(s)的最小值。设s*为极小值点,则

令 △c(s)=c(s+1)-c(s),则由(16)式得

由(15)式可得

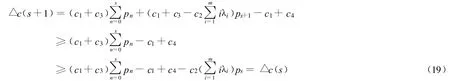
由(19)式及(17)式得:… ≤ △c(s*-2)≤△c(s*-1≤0≤ △c(s*)≤ △c(s*+1)≤… ,由 … ≤△c(s*-2)≤△c(s*-1)≤0可得:c(s*)≤c(s*-1)≤c(s*-2)≤…,由0≤△c(s*)≤△c(s*+1)≤…可得:c(s*)≤c(s*+1)≤c(s*+2)≤…,从而c(s*)为最小值。从以上推导也可以看出求最优存储量s*的计算方法:从s=1开始分别计算△c(s)的值,使 △c(s)第一次变为非负值时的s即为所求的最优存储量s*。

由于 △c(s)≥0,所以从s=1开始逐个计算(6*)右端的值,直到其变为正值,则此时对应的s值即为最优存储量(记为s*),因为当s≥s*时,△c(s)≥0,且(6*)式右端随s增大时非降,即有c(s*)≤c(s*+1)≤c(s*+2)≤…。

例 c1=2,c2=2,c3=4,c4=1,m=3,N=5,λ1=3,λ2=2,λ3=1,μi=iμ,i=1,2,3,μ=2,μ3=μ4=μ5。

解 将题设数据代入(12)～(14)式可得:p0=0.031,p1=0.273,p2=0.163,p3=0.214,p4=0.275,p5=0.044,又时,令(20)式右端为 φ(s), φ(1)=-12.52 ＜0, φ(2)=-9.26＜0,φ(3)=-6.92＜0,φ(4)=0.56＞0,所以s=4为最优存储量。

[1] 顾庆凤.具有Bernoulli反馈的M/M/1/N工作休假排队系统[J].成都信息工程学院学报,2011,26(1):52-56.

[2] 曹永荣.基于现场服务排队近似M/G/m模型的CSR配置[J].重庆师范大学学报(自然科学版),2010,27(4):36-40.

[3] 彭懿,杨向群,吴锦标.带负顾客和不耐烦顾客的离散时间Geo/G/1重试排队[J].系统工程理论与实践,2011,31(12):2372-2379.

[4] 潘全如,朱翼隽.排队论在收费站设计与管理中的应用[J].运筹学学报,2009,13(3):95-102.

[5] 孟玉珂.排队论基础及应用[M].上海:同济大学出版社,1989.

[6] 何鲲,鹿泉育.考虑可变库存费和销售机会损失的库存模型[J].合肥工业大学学报(自然科学版),2010,33(11):1717-1720.

[7] 谭畅.具有可变输入率的M/M/1排队系统的研究[J].贵州大学学报(自然科学版),2008,25(5):445-448.

[8] 王晓.有多类顾客且转移率与状态相依的排队网络设计[J].晋中学院学报,2011,28(3):71-75.

[9] 徐祖润,李敏捷.带有负顾客和强占优先权的不耐烦信员排队[J].数学的实践与认识,2010,40(23):142-148.

[10] 李乃文,崔群法,译.运筹学-概率模型应用范例与解法[M].北京:清华大学出版社,2006.

[11] 谢锦山,陈德南.仓库容量有限条件下的离散型随机存贮管理策略[J].龙岩学院学报,2010,28(5):15-18.

[12] 何鲲,鹿泉育.考虑可变库存费和销售机会损失的库存模型[J].合肥工业大学学报(自然科学版),2010,33(11):1717-1720.