一类非线性波动方程的新的精确解

刘世杰, 周钰谦, 皮金鑫

(成都信息工程学院数学学院,四川成都610225)

0 引言

随着现代科学技术的发展,越来越多复杂的现象都可以用非线性波动方程来描述。例如流体力学,光电通信,大气环流等。因此寻求新的解决问题的方法就势在必行。近些年来许多行之有效的方法被提出如,sine-cosine展开法[1],齐次平衡法[2],Darbour变换法[3],截断的Painleve展开法[4],Jacobi椭圆函数展开法[5],tanh函数展开方法及其推广方法[6],双曲正切函数展开法[7]等。现在应用较为广泛的是王明亮提出的(G′/G)展开法[8-11],使用起来简洁,高效。

文中研究的非线性波动方程[12]

当k=1,q=0时方程变形为著名的Klein-Gordon方程utt-uxx+pu+su3=0.当p=0,q=m2,s=g2时方程变形为著名的Landou-Ginburg-Higgss方程utt-uxx-m2u+g2u3=0.

主要借助改进的(G′/G)展开法[10]来求解方程(1)。首先介绍改进的(G′/G)展开法。

1 预备知识

考虑非线性发展方程

其中 x,t为自变量,H为u及u的偏导数的多项式。为了得到方程的(2)的行波解,做一个行波变换u(x,t)=U(ξ),ξ=x+ct则方程可化为

设方程(3)的解的形式为

其中G(ξ)满足二阶常微分方程

由方程(5)易得,当 G′(ξ)≠0时,

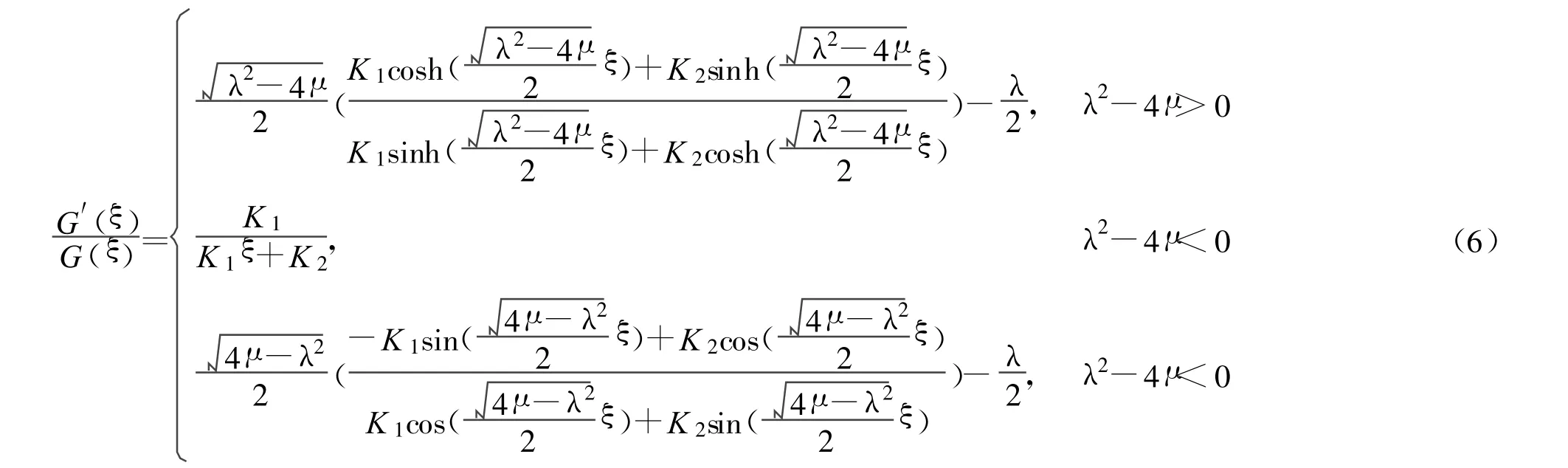
2 用改进的(G′/G)方法求解非线性波动方程

首先对方程(1)作行波变换 ξ=x+ct.令 u(x,t)=U(ξ),则方程(1)化为

平衡方程(7)中的最高阶导数项U″与非线性项U3,得到平衡系数n=1,由方程(4),则可以令方程的解为:

将解(8)带入方程(7)中,得到方程(7)中的各项为

将(8)、(9)、(10)、(11)式代入方程(7),合并的同类项,并令其同次幂为0。则得到关于a1,b1,c0,λ,μ的代数方程组:

利用Maple软件求解以上代数方程组,得到关于a1,b1,c0,λ,μ的几组解:

为了更好地理解方程解的情况,给出第7组解的数值模拟图,不妨令K1=1,K2=2.

图1 利用Maple软件得到关于 a1,b1,c0,λ,μ的第7组解的数值模拟图

3 结论

借用改进的(G′/G)展开法求解了一类非线性方程,得到了7组不同的精确解,并单独给出了第7组解的数值模拟图。加深了对方程解的理解。

致谢:感谢成都信息工程学院科研项目(CSRF20100)对本文的资助

[1] 闫振亚.浅水波近似方程的显式精确解[J].烟台大学学报,2000,13(1):8-17.

[2] Wang M L.Solitary wave solutions for variant Boussinesq equation[J].Physics Letter A,1995,199:169-172.

[3] 范恩贵.可积系统与计算机代数[M].北京:北京科学出版社,2004.

[4] Parkes E J,Duffy B R.Traveling solitary wave solution to a compound KdV-Burgers equation[J].Physics Letters A,1997,229:217-220.

[5] 刘式适,付遵涛,刘式达.变系数非线性方程的Jacobi椭圆函数展开解[J].物理学报,2002,51:1923.

[6] Parkes E J,Duffy B R.An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations[J].Computer Physics Communication,1996,98:288-300.

[7] 李志斌,张善卿.非线性波方程准确孤立波解的符号计算[J].数学物理学报,1997,17(1):81-89.

[8] 王明亮,李志斌,周宇斌.齐次平衡原则及其应用[J].兰州大学学报,1999,98:8-16.

[9] 刘倩,周钰谦,王法官.长短波相互作用方程的精确行波解[J].四川大学学报(自然科学版),2011:524-528.

[10] 王法官,刘合春.摄动Wadati-Segur-Ablowitz方程的精确行波解[J].成都信息工程学报,2010,25(5):542-546.

[11] 刘合春,王法官.非线性发展方程的精确解[J].成都信息工程学院学报,2010,25(5):551-556.

[12] 刘煜,范立群.一类非线性波动方程新的显式精确解[J].河南科技大学学报,2008,12:83-85.