一道思考题引出的精彩
2012-12-29王德林
小学教学参考(数学) 2012年7期

在一节数学活动课上,我出示了下面的思考题:图1是用边长为1厘米的小正方形围成的图形,你能算出这个图形的周长是多少厘米吗?
全班学生冥思苦想,一时得不到答案。我本想引导学生一起分析这个图形的周长是指图中哪一部分,怎样才能算出这个图形的周长。后来转念一想,不如把探索问题的过程交给学生。
师:你能用学具盒里面1厘米的小棒在小组里摆一摆吗?
学生分小组活动。不一会儿有几个学生举起了手。
生1:根据周长的意义,把围成图形的所有边长加起来,得2+1+1+2+1+1+2+4=14厘米。
师:同意吗?
大多数同学点头同意。
生2:我们可以数围成图形的周长里面有几条1厘米的线段。一共有14条1厘米的线段,就用1×14=14厘米。
师:你能在小组里数一数吗?
学生在小组里互相数一数。
生3:如果小正方形的数目多,数起来就很麻烦。
师:看起来你还有更好的方法!
生3:我们也可以这样计算,这个图形是由6个小正方形组成的,每个正方形有4条边,一共有24条边,就是1×24=24厘米,在图形里面共有5组边重复,每组边是由相邻的两个正方形的两条边组成的,要减去10条边的长,就是要减去1×10=10厘米,然后得24-10=14厘米。
师:你的意思是先计算出6个正方形的总边长,然后减去图形里所有重复边的长度,就是这个图形的周长。
生3:对。
师:你们还能用其他方法来求这个图形的周长吗?
生4:用前面学过的平移方法计算这个图形的周长。
看到学生这么活跃,我索性顺水推舟,让学生动手用小棒移一移。
师:你能在小组里用小棒移一移吗?
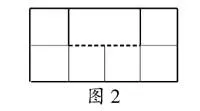
生5:不好平移,把凹进去的一条较长的线段移上去的话,得到了一个长方形c48Ryec1+n/BsEsF4G1gVfOfApU9AmCB3xNLwQJYckw=,但这个长方形的周长不等于这个图形的周长(如图2)。
师:怎么办呢?用上面平移的方法能不能计算出这个图形的周长呢?小组里面讨论一下!
生6:把凹进去较长的的线段平移上去以后,就少算了两条较短的边,计算图形的周长,如果用长方形的周长那还要加上少算了的两条边的长,得4+2=6厘米,6×2=12厘米,12+2=14厘米。
至此,学生一共得出了四种方法,教学目标基本达成,我本想小结一下,进入下一个环节的教学,突然有一个学生举起了小手。
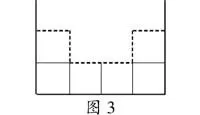
生7:我还可以把凹进去的两条较短的线段移到宽上,里面的3条线段移到长上(如图3)。这样,就把这个图形转化成规则的长方形,这个长方形的长是4厘米,宽是2+1=3厘米,得4+3=7厘米,7×2=14厘米。
全班同学响起了热烈的掌声!
【反思】我们平时的课堂,大都按照预定的设计进行教学,一节课的教学活动非常紧凑,课堂容量非常大。但本节课中我改变了原先的设计,先让学生利用学具盒里面的1厘米的小棒在小组里摆一摆,竟收到意想不到的效果,学生很快发现了三种解法,此时我并没有就此收场,而是继续提问学生:“你还能用其他方法来求这个图形的周长吗?”当有学生想到可以用前面学过的平移方法时,我顺水推舟让学生在小组里移一移,使得学生的思维步步深入,后面的精彩才如期而至。
可以设想一下,这一节课如果按原先的设计,循规蹈矩,学生就会被老师牵着鼻子走,他们的积极性就会受到影响,思维就会被禁锢起来,就不能用原来的知识去顺应新的知识。在教学中,我们面对是不同的学生,他们的真实水平往往无法准确估计。在实施具体教学的过程中,教师要根据教学的具体情况冷静思考,灵活地调整教学方法,机智生成新的教学方案。数学课堂的动态生成离不开教师的预设,教师的设计不能过于精细,教师的预设要着眼于整体、着眼于开放,同时教师的预设要富有弹性,要给学生留足空间,为学生搭建个性张扬的舞台,激活学生心中那小小的“涟漪”,激起学生在课堂上的“千层浪”,引发思维碰撞的“共鸣”,真正焕发出生态课堂的活力。
其次,这节课我让学生动手摆一摆、移一移,这不仅符合学生好奇、好动的心理特点和几何初步知识直观、操作性强的知识特点,更重要的是充分体现了以活动促发展的教学思想。整个教学过程是以学习者为中心,以学生的自主活动为基础,使学生在活动中学习,在活动中探索,在活动中发展,学生真正动了起来,课堂真正活了起来。因此在教学中我们要向学生充分提供从事数学活动的机会,帮助他们在自主探索、合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法,获得广泛的数学活动经验,使学生真正成为学习的主人。
(责编 金
