假设大正方体外面涂了一层红色的漆

　　【案例】
　　去年暑假，小姨把她家那小子送到我家来住几天。我知道她是想让我辅导他做作业。这小家伙今年五年级，很是聪明，就是最怕麻烦，对语文是喜欢动口不动手，对数学倒是很亲近。但他做数学题，常让人担心。因为他在做题时，两眼盯在试题上，嘴中念念有词，然后直接在题后写上答案。这不免让人怀疑是不是在蒙。但每次检查时，又少有差错。
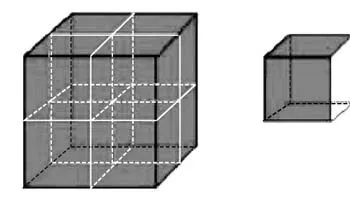
　　他的《暑假作业》中有这样一道题：一个正方体，表面积是96平方厘米，现在将它平均分成大小相同的8个小正方体，每个小正方体的表面积是多少？
　　他在做这道题的时候，又和往常那样两眼盯在试题上，嘴中念念有词了。我不言语，看他怎样做这一题。同时自己也想好了这道题的解题方法：（1）求出大正方体每个面的面积：96÷6=16（平方厘米），从而求出大正方体的棱长是4厘米。（2）求出每个小正方体的棱长：4÷2=2（厘米）。（3）求出每个小正方体的表面积：2×2×6=23b4c6f8d2768b8c9c3c47cacb9abe2a14（平方厘米）。
　　几乎在我想好的同时，他也写出了算式和答案：96÷8×2=24（平方厘米）。
　　看着他写的算式，我想了很长时间，也想不出这个算式表达的意义。于是我笑着对他说：“你的答案是正确的，但式子表示什么意义呢，别是蒙的吧？”
　　他一本正经地对我说：“我不是蒙的，我是这样想的：假设大正方体外面涂了一层红色的漆，平均分成八个大小相同的正方体后，每个小正方体就有三个面是红色的。而一个正方体有六个相等的面，所以只要再乘2就是每个小正方体的表面积了。”小家伙边说还边画出了如下示意图。
　　【思考】
　　孩子为什么要在大正方体外面涂上一层红色的漆呢？他是怎么想到用红漆去涂正方体的外面的？孩子当初想到在外面涂漆有什么用途？孩子是不是受线索词“表面积”的启发而下意识地想到了涂漆呢？
　　【分析】
　　孩子可能的想法：1.受线索词“表面积”的启发及教材中“粉刷墙壁”经验的积累。由线索词“表面积”联系到教材中的内容“粉刷墙壁”。如果是这样，那么涂漆的做法是源于教材与生活的经验积累的一种再创造。2.孩子是受其他的经验的启发。一开始并不知道涂漆对解决问题有用，在接下来的思考和探索中受启发才从涂漆中找到解决问题的方法。3.孩子是为了表达时让别人明白自己的解法的需要才想到涂漆的。
　　这些分析结果都需要进一步向孩子求证。第二天，就这些问题我再次向他提问。面对我的追问，小家伙倒不拘谨：“我是从正方体有八个顶点开始思考的，平均分成八个小正方体，应该每个小正方体都含有一个原来大正方体的一个顶点，而围成这个顶点的三个面就是露在外面的面。”一边说，一边翻开教材（新世纪小学数学第十册“长方体（一）——露在外面的面”P20）。
　　“那你为什么要在大正方体外面漆上一层红漆呢？”
　　“涂上一层红漆后，会使原来露在外面的面积和切开后的面积之间的关系变得更加直观。同时也方便我向你说明我的解题思路。”
　　我分析孩子在面上涂漆是解决问题或表达的需要，是截然分开的，但孩子的回答似乎在告诉我们，他的分界并没有这么清楚。他把大的立方体涂漆既是思考问题的需要，又是他表达的需要。从这一点上看，国外的研究认为学生在解决问题时，是先表征，再考虑解决的策略是正确的。
　　【启示】
　　从上面的案例我们可以得到如下启示：第一，基本活动经验的积累有利于学生在解决问题时准确把握问题的本质。
　　孩子一开始并没有受“表面积是96平方厘米”的影响，而是“从正方体怎么分为八个小立方体”开始思考，他关注到正方体由大到小的变化。而在关注变化的同时，他在寻找不变的东西，并与以往学过的经验相联系。涂漆的经验帮助他思考问题并成功地解决了问题，同时为他表达解题思路提供了便利。
　　第二，利用几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。
　　孩子在关注变化的同时，紧紧捕捉住不变的东西，那就是他发现了“要求的八个小正方体的表面积比原来的大正方体的表面积多，且要求的八个正方体的表面积等于原大正方体的表面积再加上新增的表面积”。对“变化中的不变”的把握，他是通过涂漆的方法直观实现的。而且这种思路较常规思路更为简明、形象。这与《全日制义务教育数学课程标准》修订版中提出的几何直观概念非常一致。
　　（责编　黄春