探究数学本质 展示数学魅力

　　教学目标：
　　1．会用折纸等方法确定轴对称图形的对称轴，进一步体会轴对称图形的特征，能画出一些简单轴对称图形的对称轴。
　　2．初步学会运用对称的方法在方格纸上设计轴对称图案，进一步增强空间观念。
　　3．在认识对称的过程中，进一步感受美、理解美，增强学习数学的兴趣。
　　教学过程：
　　一、创设情境，感知对称
　　1．师：同学们，上课前，老师带来了几张美丽的图片，想欣赏一下吗？（想）好，一起来看看。（电脑配乐出示蝴蝶、树叶、蜻蜓的图片）
　　2．师：如果我们从数学的角度来研究它们的话，这三幅图片在外形上有什么共同的特征？（引导得出轴对称图形，并板书课题）
　　3．结合图片及动画引导学生回顾轴对称图形和对称轴的概念，并板书关键词“对折”“完全重合”。
　　4．师：是啊，生活中正是有了这些对称现象，才使我们的生活如此美丽。其实，对称现象在我们数学世界里也有很多，今天我们就一起来继续研究轴对称图形。
　　【反思：课始，让学生在音乐声中欣赏并回忆轴对称图形的概念，使学生在轻松愉快的情境中产生进一步求知的欲望。】
　　二、引导探索，研究对称
　　1．研究长方形。
　　师：长方形是轴对称图形吗？有几条对称轴？（学生有的认为是2条，有的认为是4条，引导学生拿出长方形纸折一折、数一数，汇报时先让认为长方形有4条对称轴的学生说一说，从而引发争论，最后得出长方形有2条对称轴）
　　师：刚才我们用折纸的方法，找到了长方形有2条对称轴，你能画出黑板上这个长方形的对称轴吗？（学生介绍方法，教师电脑演示）
　　师（提示）：对称轴一般用点画线表示；因为对称轴是折痕所在的直线，所以要画的比原来长一些。
　　2.研究正方形。
　　师：正方形是轴对称图形吗？有几条对称轴？请你画出它的4条对称轴。（学生画完后，师通过电脑进行验证）
　　3．研究其他平面图形是不是轴对称图形。
　　师：同学们，在我们学过的平面图形中，除了长方形、正方形是轴对称图形外，还有别的图形是轴对称图形吗？
　　（1）师：我们以小组为单位进行探讨。在三角形、梯形、平行四边形三种图形中，每小组选择一种图形进行全面深入的研究，然后我们全班交流讨论。
　　（2）研究提示。
　　①通过折一折，判断这种图形是不是轴对称图形。
　　②是轴对称图形的画出它的对称轴。
　　③认真做好记录，准备汇报。
　　（3）师：小组迅速讨论一下，选择哪种图形，讨论好以后，组长上来取图形。
　　（4）小组研究，教师参与到学生中进行适当指导。
　　（5）师（在学生汇报每一种图形后）：关于 是不是轴对称图形，你们有什么话想说？（使学生对这种图形形成科学的、完整的认识）
　　4．研究圆。
　　师：老师还带来了一个被称为最完美的图形——圆，圆是轴对称图形吗？有多少条对称轴？（在学生回答后，师通过课件进行验证）
　　5．研究正多边形对称轴的条数与边数的关系。
　　师：同学们，在我们学过的平面图形中，不但有很多是轴对称图形，并且有的轴对称图形里还蕴含着有趣的规律。
　　电脑逐步呈现：
　　（1）等边三角形又叫正三角形，正三角形有3条对称轴。
　　（2）正方形又叫正四边形，正四边形有多少条对称轴？
　　（3）正五边形，有多少条对称轴？（学生有的猜5条，有的猜1条）
　　师：正五边形到底有多少条对称轴，请大家来折一折、数一数。（学生折，并一起数，最后确定正五边形有5条对称轴）
　　（4）师：大家大胆猜想一下，正六边形有多少条对称轴？正七边形呢？正十边形呢……你发现了什么？
　　师（引导得出）：正多边形对称轴的条数和它的边数（或角数）相等。
　　（5）师：正十边形有多少条对称轴？正一百边形？圆呢？
　　师（小结）：其实，最初的圆就是通过正多边形不断切割而成的。同学们，现在知道圆为什么有无数条对称轴了吗？
　　【反思：这个环节研究对称图形体现了如下的特点：1.突出基础知识，使数学回归本质。研究长方形按“是不是轴对称图形——有几条对称轴——开展验证——画对称轴”的程序进行，使学生从折（感性）中找对称轴到画（理性）中找对称轴，从而掌握轴对称图形的本质。2.自主探索体现开放性。在研究其他图形是不是轴对称图形的教学中，教师让学生自由选择自己研究的对象，体现了自主性，并且充分放手让学生通过折、画等方式系统地认识哪些图形是不是轴对称图形，是轴对称图形的有几条对称轴。3.探索规律，展示数学的魅力。在探索正多边形有几条对称轴的过程中，教师首先让学生找出正多边形的所有对称轴，再引导学生观察，并找出规律，培养了学生的观察推理能力，更重要的是利用“割圆术”和极限的思想让学生了解了圆为什么有无数条对称轴的深刻内涵，使学生感受到数学的魅力就在于它是有规律可循的。】
　　三、放飞想象，创造对称
　　师：是啊，数学的魅力就在于去探索和发现它的基本规律，并运用它来创造生活的美。下面，就让我们放飞想象的翅膀，大胆地去创造吧。
　　1．根据轴对称图形的左半边，想象它的右半边，并判断是什么图案。（中国联通的标志）
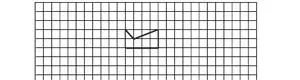
　　2．画出下面图形的另一半，使它成为轴对称图形。
　　
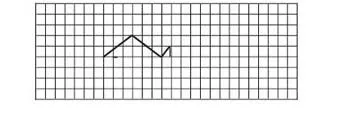
　　3．先自主确定一条对称轴，再画出下面图形的另一半，使它成为轴对称图形。
　　【反思：练习设计以想象为主题，由浅入深分三个层次。教师首先利用学生熟悉的轴对称图案的一半，让学生想象它的另一半，并判断它是什么标志，初步培养学生的想象能力。然后，教师引导学生根据轴对称图形的一半，想象它的另一半并画出来，这不仅培养了学生的想象能力，而且培养了学生的动手操作能力。最后，教师引导学生由封闭想象到开放想象，并创作想象图形，充分体现了个性化的教学设计理念，注意培养学生的创新精神，使学生的潜能得到进一步的培养和升华。】
　　四、走进生活，欣赏对称
　　师：看来，轴对称图形真是奥妙无穷啊！其实，我们数学上的对称在生活中也有广泛的应用。（电脑出示：舞蹈家利用对称的性质，创作了美丽的《千手观音》；建筑师运用对称的思想，建造了庄严的宫殿；蝴蝶、蜻蜓翅膀的对称是为了平衡的需要，科学家受到启发，设计出的飞机才能平稳地飞翔在蓝天……）
　　师：同学们，感觉怎么样？美吗？
　　师：这不正是轴对称图形的魅力所在吗？那就让我们从现在起，用心去观察、研究生活中的对称现象，好吗？
　　【反思：让学生欣赏生活中用轴对称现象创造的美，体现了数学的应用价值，激励并启发学生不断探究的激情和欲望，从而达到了“课虽尽，而意无穷”的教学境界。】
　　邱学华老师说过：“要用数学本身的魅力去吸引学生。”在本节课中，教师设计了四个环节，让学生在“感知——研究——创造——欣赏”的活动中真正感受到探究数学的乐趣，更重要的是让学生在数学活动中体验到了数学知识的魅力，感受到了数学之美。美的东西总是让人过目不忘，让人由衷喜欢的，教学更是如此。在本课中，教师从学生对对称美的一般感受到对对称美的理解，再到创造具有对称美的作品，都体现了教师创造性的教和学生创造性的学的有机结合，学生的数学学习过程充满了对数学之美的享受。
　　（责编　杜