A New System of Generalized Variational Inclusions Involving H-η-monotone Operators in Uniformly Smooth Banach Spaces∗

FENG SHI-QIANG AND GAO DA-PENG

(School of Mathematics and Information,China West Normal University, Nanchong,Sichuan,637002)

A New System of Generalized Variational Inclusions InvolvingH-η-monotone Operators in Uniformly Smooth Banach Spaces∗

FENG SHI-QIANG AND GAO DA-PENG

(School of Mathematics and Information,China West Normal University, Nanchong,Sichuan,637002)

In this paper,we introduce and study a new system of generalized variational inclusions involvingH-η-monotone operators in uniformly smooth Banach spaces.Using the resolvent operator technique associated withH-η-monotone operators,we prove the approximation solvability of solutions using an iterative algorithm. The results in this paper extend and improve some known results from the literature.

uniformly smooth Banach space,H-η-monotone operator,resolvent operator technique,system of generalized variational inclusion,iterative algorithm

1 Introduction

Variational inequalities and variational inclusions are among the most interesting and important mathematical problems and have been studied intensively in the past years since they have wide applications in mechanics,physics,optimization and control,nonlinear programming,economics and transportation equilibrium,and engineering sciences,etc.(see, for example,[1–22]).Various kinds of iterative algorithms for solving the variational inequalities and inclusions have been developed by many authors.For details,we can refer to [1–20]and the references therein.Among these methods,the resolvent operator techniques for solving variational inequalities and variational inclusions are interesting and important.

On the other hand,monotonicity techniques were extended and applied in recent years because of their importance in the theory of variational inequalities,complementarity problems,and variational inclusions.In[1–3],Huanget al.introduced several kinds of mono-tone operators,which gradually extendedη-subdifferential operators,maximalη-monotone operators andH-monotone operators.They also studied some classes of varational inclusions using the resolvent operators associated with related monotone operators.Fang and Huang[4]further introduced a new class of generalized monotone operators,(H,η)-monotone operators,which provided a unifying framework for classes of maximal monotone operators, maximalη-monotone operators,andH-monotone operators.They also studied a class of variational inclusions using the resolvent operator associated with an(H,η)-monotone operator.Louet al.[5]extended the concept of resolvent operators associated with(H,η)-monotone operators to newH-η-monotone operators.By using the new resolvent operator technique,they studied a system of variational inclusions involvingH-η-monotone operators in Banach spaces.Motivated and inspired by the above works,in this paper,we explore the approximation solvability of a new system of generalized variational inclusion problems based onH-η-monotone resolvent operator techniques.Our results improve and extend the rencent ones.

2 Preliminaries

LetEbe a real Banach space equipped with the norm.Denote by〈·,·〉the dual pair betweenEand its dual spaceE∗,by 2Ethe family of all nonempty subsets ofE,and byCB(E)the family of all nonempty closed and bounded subsets ofE.LetD(·,·)be the Hausdor ffmetric onCB(E)de fi ned by

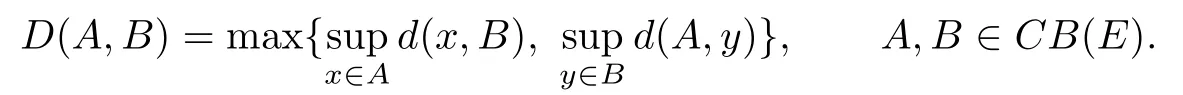
LetJ:E−→be the normalized duality mapping de fi ned by

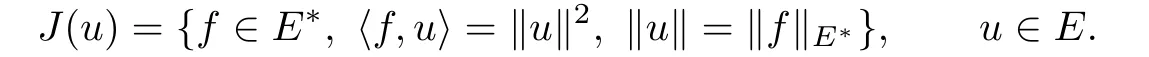
It is well known that ifEis smooth,thenJis single valued,and ifE≡H,a Hilbert space, thenJis an identity mapping.

The following concepts and results are needed in the sequel.

De fi nition 2.1[6]Let P:E−→E∗,g:E−→E,and η:E×E−→E be single-valued mappings.Then

(1)P is said to be α-strongly η-monotone if there exists a constant α＞0such that

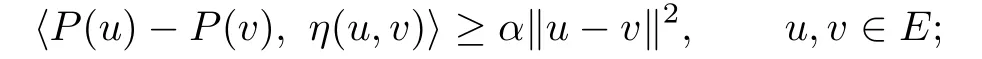
(2)g is said to be k-strongly accretive,if there exists a constant k＞0such that

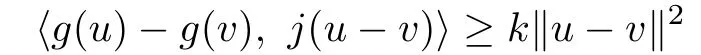
for any u,v∈E,j(u−v)∈J(u−v),where j is a selection of set-valued mapping J;

(3)η is said to be τ-Lipschitz continuous,if there exists a constant τ＞0such that

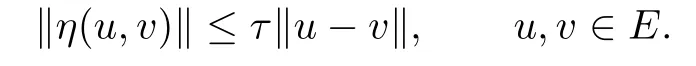
De fi nition 2.2[4]Let T:E−→E∗be a single-valued operator.Then the operator T is said to be

(1)monotone if〈Tx−Ty,x−y〉≥0for any x,y∈E;

(2)strictly monotone if T is monotone and〈Tx−Ty,x−y〉=0if and only if x=y;

(3)strongly monotone if there exists a constant r＞0such that

(4)Lipschitz continuous if there exists a constant s＞0such that kTx−Tyk≤skx−yk.De fi nition 2.3[4]Let M:E−→be a multi-valued operator,H:E−→E∗and η:E×E−→E be single-valued operators.Then M is said to be

(1)monotone if〈x−y,u−v〉≥0for any u,v∈E,x∈Mu and y∈Mv;

(2)η-monotone if〈x−y,η(u,v)〉≥0for any u,v∈E,x∈Mu and y∈Mv;

(3)strongly η-monotone if there exists a constant r＞0such that

(4)m-relaxed η-monotone if there exists some constant m＞0such that

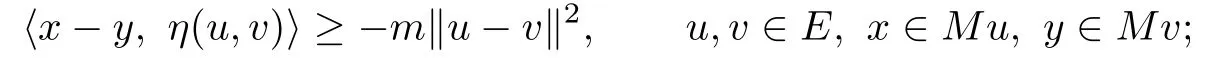
(5)maximal monotone if M is monotone and has no a proper monotone extension in E,i.e.,for any u,v0∈E and x∈Mu,〈x−y0,u−v0〉≥0implies y0∈Mv0;

(6)maximal η-monotone if M is η-monotone and has no proper η-monotone extension in E;

(7)H-monotone if M is monotone and(H+λM)E=E∗for λ＞0;if M is η-monotone and(H+λM)E=E∗for λ＞0,then M is said to be an(H,η)-monotone operator;

(8)H-η-monotone if M is m-relaxed η-monotone and(H+λM)E=E∗for λ＞0.

Remark 2.1Maximalη-monotone operators,H-monotone operators,and(H,η)-monotone operators were first introduced by Huang and Fang[7],H-η-monotone operators were introduced by Zhang[8].Obviously,the class ofH-η-monotone operator is more extensive than the above.For details about these operators,we refer the reader to[4,7–8]and the references therein.

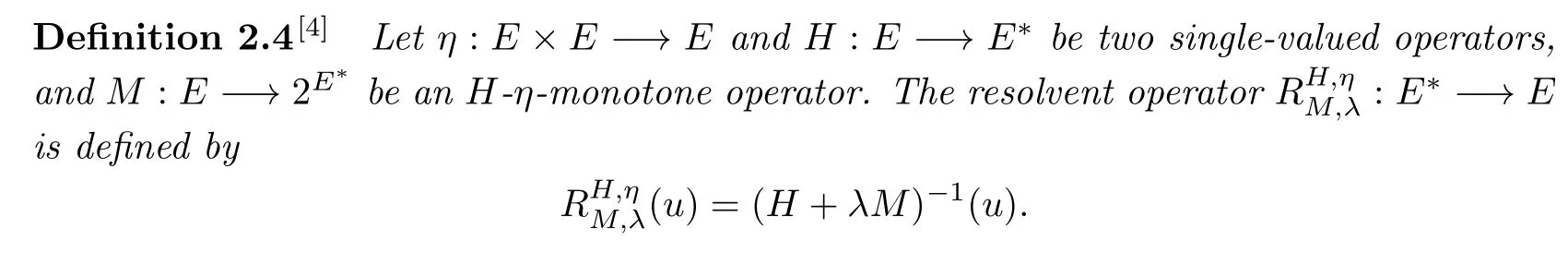
De fi nition 2.5Let E be a real Banach space,and A:E−→CB(E)be a set-valued mapping.A is said to be D-Lipschitz continuous,if there exists a constant t＞0such that

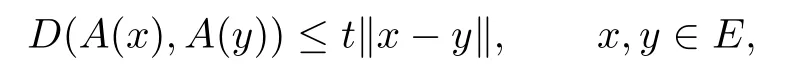
where D(·,·)denotes the Hausdor ffmetric on CB(E).

Theorem 2.1Let E be a real Banach space,η:E×E−→E be a Lipschitz continuous operator with constant τ＞0,H:E−→E∗be a strongly η-monotone operator with constant r＞0,and M:E−→be a multi-valued H-η-monotone operator.Then,the resolvent

:E∗−→E is Lipschitz continuous with constantforthat is,

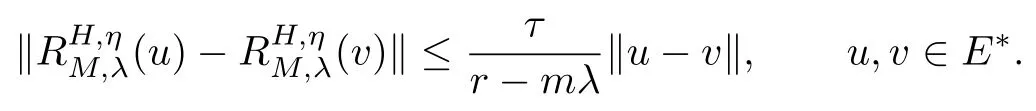
Lemma 2.1[9]Let E be a real uniformly smooth Banach space,and J:E−→E∗be the normalized duality mapping.Then,for all u,v∈E,

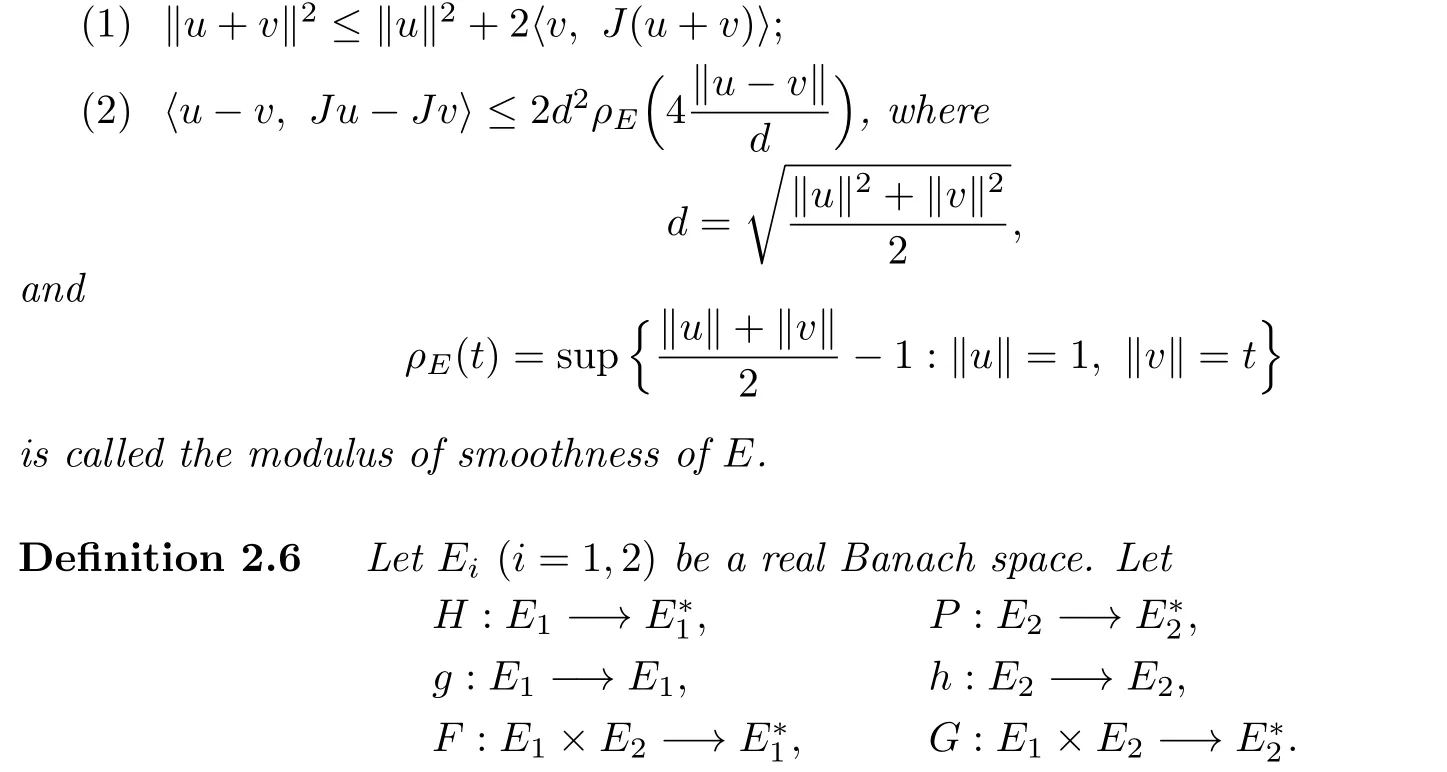
Then

(1)F is said to be locally α-strongly accretive with respect to H0g in the first argument if there exists a constant α＞0:1is a normalized duality mapping;

(2)G is said to be locally β-strongly accretive with respect to P0h in the second argument, if there exists a constant β＞0such that

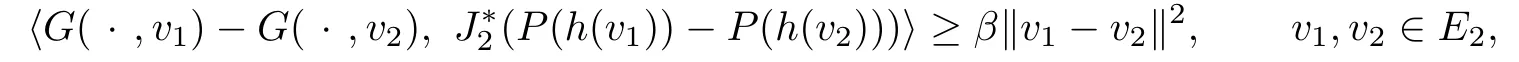
:2is a normalized duality mapping;

(3)F is β1-Lipschitz continuous in the first argument if there exists a constant β1＞0such that

(4)G is β2-Lipschitz continuous in the second argument,if there exists a constant β2＞0such that

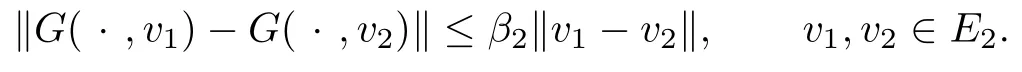
3 A New System of Generalized Variational Inclusions

In this section,we introduce a new system of variational inclusions involving monotone operators in uniformly smooth Banach spaces.In what follows,unless otherwise speci fi ed, we always assume thatE1andE2are two real Banach spaces,

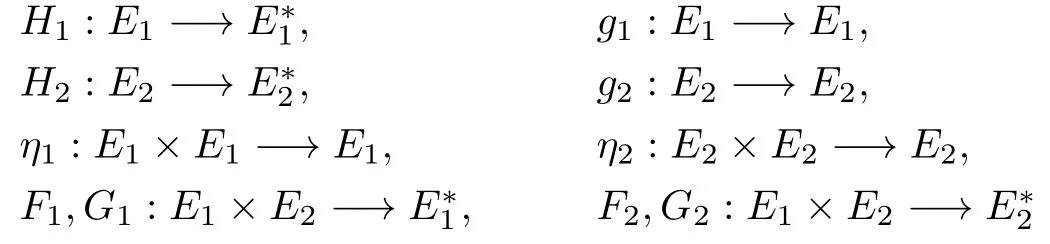
are all single-valued mappings and

are all set-valued mappings.LetM1:E1−→be anH1-η1-monotone mapping andM2:E2−→be anH2-η2-monotone mapping.

For any given(f,h),we consider the following problem of finding(x,y,a,b,p,q) such that(x,y)∈E1×E2,a∈A(x),b∈B(y),p∈P(x),q∈Q(y)and

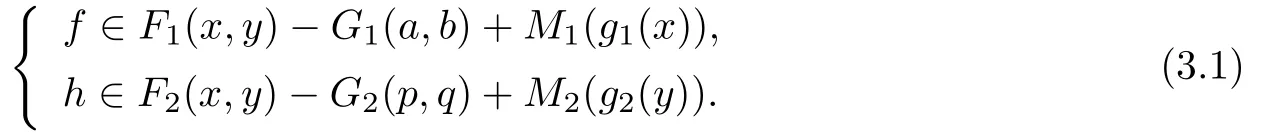
Note that for appropriate choices of the mappingsFi,Gi,Mi,gi(i=1,2),it is easy to see that the problem(3.1)includes many nonlinear systems of variational inclusions (inequalities)as special cases;see[4–5,15,20]and the references therein.

In this section,we consider the solvability of the above system of generalized variaitonal inclusions using the generalized resolvent operator technique.

Lemma 3.1For i=1,2,let ηi:Ei×Ei−→Eibe a single-valued mapping,gi:Ei−→Ei be a single-valued mapping,and Hi:Ei−→be a strongly ηi-monotone operator with constant ri.Let Mi:Ei−→be Hi-ηi-monotone.Then(x,y,a,b,p,q)with(x,y)∈E1×E2,a∈A(x),b∈B(y),p∈P(x),q∈Q(y)is a solution of the problem(3.1)if andonly if

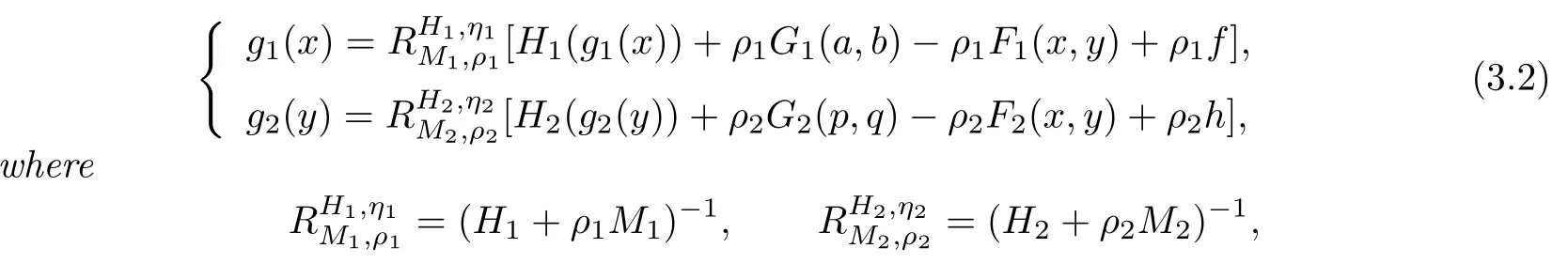
ρ1＞0and ρ2＞0are two constants.

Proof.The fact directly from De fi nition 2.4 and Theorem 2.1.

The relation(3.2)and Nadler’s theorem of[10]allow us to suggest the following iterative algorithm.

Algorithm 3.1For any givenx0∈E1andy0∈E2,we can compute the sequences{xn},{yn},{an},{bn},{pn}and{qn}by the iterative schemes

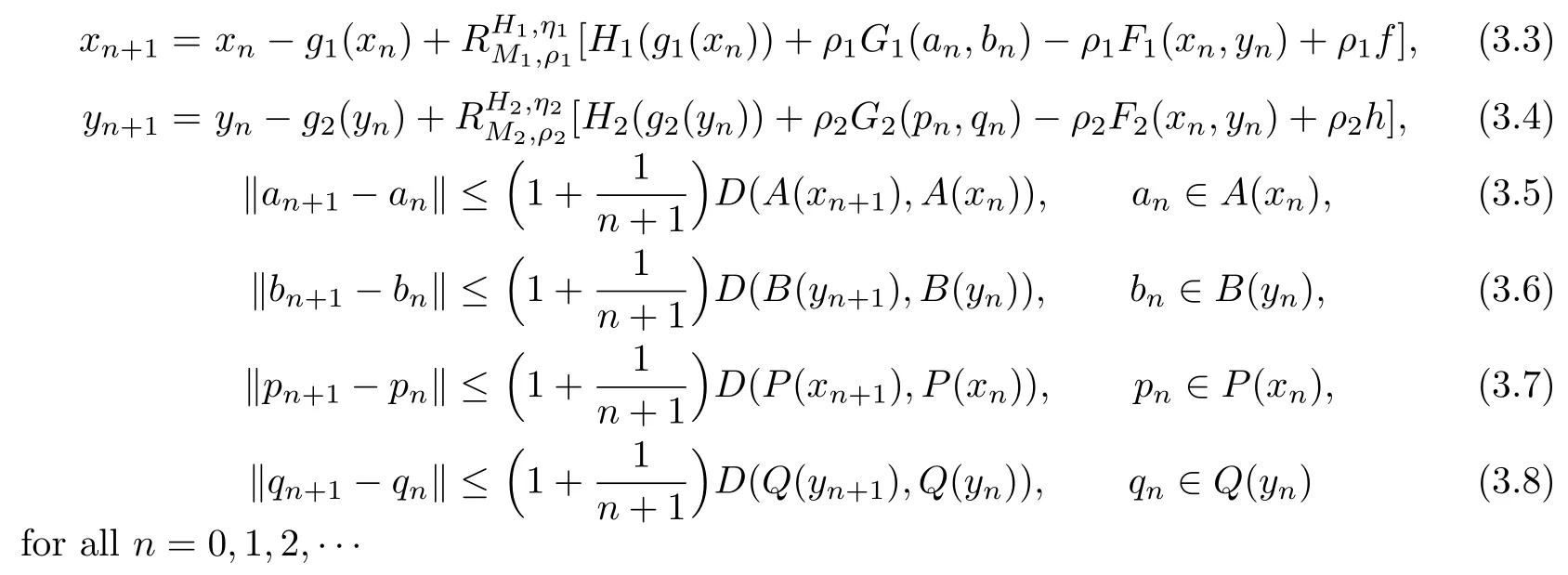
4 Existence of Solutions and Convergence of an Iterative Algorithm

In this section,we prove the existence of solutions for the problem(3.1)and the convergence of iterative sequence generated by Algorithm 3.1.

Theorem 4.1For i=1,2,let

Eibe a real uniformly smooth Banach space with ρEi(t)≤cit2for some ci＞0;

ηi:Ei×Ei−→Eibe a Lipschitz continuous operator with constant τi＞0;

Hi:Ei−→be a strongly ηi-monotone operator with constant ri＞0and be a σi-Lipschitz continuous operator;

gi:Ei−→Eibe ki-strongly accretive andµi-Lipschitz continuous;

A,P:E1−→CB(E1),B,Q:E2−→CB(E2)be D-Lipschitz continuous with constant lA＞0,lP＞0,lB＞0and lQ＞0,respectively;

F1:E1×E21-Lipschitz continuous in the first variable,and γ1-Lipschitz continuous in the second variable and F1(·,b)be locally α-strongly accretive with respect tog1with constant α in the first argument;

G1:E1×E21and ω1,respectively;

F2:E1×E22-Lipschitz continuous in the second argument and γ2-Lipschitz continuous in the first argument and F2(a,·)be locally β-strongly accretive with respect to H02g2with constant β in the second argument;

G2:E1×E22and ω2,respectively;

Mi:Ei−→be a multi-valued Hi-ηi-monotone operator. Suppose that there exist constants ρ1and ρ2such that

Then the problem(3.1)admits a solution(x,y,a,b,p,q)and the sequences{xn},{yn},{an}, {bn},{pn},{qn}converge to x,y,a,b,p,q,respectively,where{xn},{yn},{an},{bn}, {pn},{qn}are the sequences generated by Algorithm3.1.

Proof.Let

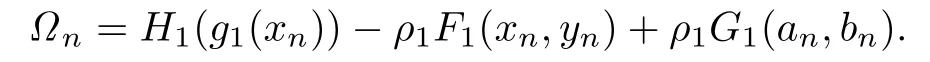
By(3.3)and Theorem 2.1,we have

It follows from the Lipschitz continuity ofG1,theD-Lipschitz continuity ofAandB,and (3.5)-(3.6)that

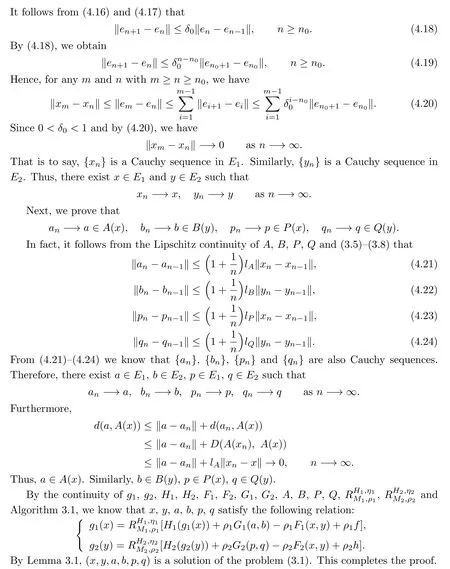
[1]Huang N J,Fang Y P.A new class of general variational inclusions involving maximalηmonotone mappings.Publ.Math.Debrecen,2003,62:83–98.

[2]Ding X P,Luo C L.Perturbed proximal point algorithms for generalized quasi-variational-like inclusions.J.Comput.Appl.Math.,2000,210:153–165.

[3]Fang Y P,Huang N J.H-monotone operator and resolvent operator technique for variational inclusions.Appl.Math.Comput.,2003,145:795–803.

[4]Fang Y P,Huang N J.A new system of variational inclusions with(H,η)-monotone operators in Hilbert spaces.Comput.Math.Appl.,2005,49:365–374.

[5]Lou J,He X F,He Z.Iterative methods for solving a system of variational inclusions involvingH-η-monotone operators in Banach spaces.Comput.Math.Appl.,2008,55:1832–1841.

[6]Kazmi K R,Bhat M I.Convergence and stability of iterative algorithms of generalized setvalued variational-like inclusions in Banach spaces.Appl.Math.Comput.,2005,166:164–180.

[7]Huang N J,Fang Y P.Fixed point theorems and a new system of multivalued generalized order complementarity problems.Positivity,2003,7:257–265.

[8]Zhang Q B.Generalized implicit variational-like inclusion problems involvingG-η-monotone mappings.Appl.Math.Lett.,2007:20:216–221.

[9]Ding X P.Generalized quasi-variational-like inclusions with nonconvex functionals.Appl.Math. Comput.,2001,122:267–282.

[10]Nadler S B.Multivalued contraction mapping.Paci fi c J.Math.,1969,30:457–488.

[11]Kazmi K R,Khan F A.Parametric general variational-like inequality problem in uniformly smooth Banach space.Article ID:42451,pages 1–13,doi 10.1155/FPTA/2006/42451,2006.

[12]Zhou Y,Chang S S.Convergence of implicit iteration process for a finite family of asymptotically nonexpansive mappings in Banach spaces.Numer.Funct.Anal.Optim.,2002,23: 911–921.

[13]Chang S S,Cho Y J,Zhou H Y.Iterative Methods for Nonlinear Operator Equations in Banach Spaces.New York:Nova.Sci.Publ.,2002.

[14]Chang S S.Some results for asymptotically pseudo-contractive mappings and asymptotically nonexpansive mappings.Proc.Amer.Math.Soc.,2001,129:845–853.

[15]He Z Q,Chang S S.A system of nonlinear variational-like inclusions withη-monotone mappings in Hilbert spaces.Indian J.Math.,2009,51:511–522.

[16]Verma R U.A system of generalized auxiliary problems principle and a system of variational inequalities.Math.Inequal.Appl.,2001,4:443–453.

[17]Verma R U.Projection methods,algorithms,and a new system of nonlinear variational inequalities.Comput.Math.Appl.,2001,41:1025–1031.

[18]Verma R U.Generalized system for relaxed cocoercive variational inequalities and projection methods.J.Optim.Theory Appl.,2004,121:203–210.

[19]Chidume C E,Zegeyea H,Kazmi K R.Existence and convergence theorems for a class of multi-valued variational inclusions in Banach spaces.Nonlinear Anal.,2004,59:649–656.

[20]Peng J W,Zhu D L.Three-step iterative algorithm for a system of set-valued variational inclusions with(H,η)-monotone operators.Nonlinear Anal.,2008,68:139–153.

[21]Giannessi F,Maugeri A.Variational Inequalities and Network Equilibrium Problems.New York:Plenum,1995.

[22]Jung J S,Morales C H.The Mann process for perturbedm-accretive operators in Banach spaces.Nonlinear Anal.,2001,46:231–243.

Communicated by Ji You-qing

49J40,47H10,47H19

A

1674-5647(2012)04-0324-13

date:Feb.15,2011.

The NSF(60804065)of China and the Foundation(11A028)of China West Normal University.