A Joint Density Function in Phase-type(2) Risk Model∗

XU HUAIAND TANG LING

(1.School of Mathematics,Anhui University,Hefei,230039)

(2.Department of Mathematics,Anhui Institute of Architecture and Industry, Hefei,230601)

A Joint Density Function in Phase-type(2) Risk Model∗

XU HUAI1AND TANG LING2

(1.School of Mathematics,Anhui University,Hefei,230039)

(2.Department of Mathematics,Anhui Institute of Architecture and Industry, Hefei,230601)

In this paper,we consider a Gerber-Shiu discounted penalty function in Sparre Andersen risk process in which claim inter-arrival times have a phase-type(2) distribution,a distribution with a density satisfying a second order linear differential equation.By conditioning on the time and the amount of the first claim,we derive a Laplace transform of the Gerber-Shiu discounted penalty function,and then we consider the joint density function of the surplus prior to ruin and the de ficit at ruin and some ruin related problems.Finally,we give a numerical example to illustrate the application of the results.

Gerber-Shiu discounted penalty function,phase-type(2)distribution, surplus prior to ruin,de ficit at ruin

1 Introduction

The Sparre Andersen surplus process{U(t)}t≥0is de fi ned by

LetTdenote the time of ruin.|UT|andUT−denote the de ficit at ruin and the surplus prior to ruin,respectively.Let

wherew(·,·)is a non-negative function,and

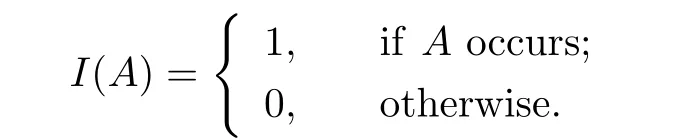
We remark that our functionφ(u)is a simple version of the more general Gerber-Shiu discounted penalty function

We setδ=0 simply in this paper.The Gerber-Shiu function is well recognized in risk model.Landriault and Willmot[1]considered the Gerber-Shiu function in the Sparre Andersen model with an arbitrary interclaim time distribution.Zhao and Yin[2]studied the Gerber-Shiu expected discounted penalty function for Levy insurance risk process.Cheunget al.[3]considered some structural properties of Gerber-Shiu expected discounted penalty function in dependent Sparre Andersen model.By the Markov property of a joint process, Songet al.[4]proved the systems of integro-differential equations for the Gerber-Shiu functions and obtained closed form expressions for the Gerber-Shiu functions when the claim amount distribution is from the rational family.

In this paper,we present the expression ofφ(u)in Sparre Andersen risk model with phase-type(2)inter-claim time.In Section 2,we introduce some preliminary results about the phase-type distributions.In Section 3,by conditioning on the time and the amount of the first claim,we derive a Laplace transform of the Gerber-Shiu discounted penalty functionφ(u),and then we consider the joint density function of the surplus prior to ruin and the de ficit at ruin and some ruin related problems.Finally,in Section 4,we give a numerical example to illustrate the application of the results.

2 Phase-type Distributions

Phase-type distributions have become an extremely popular tool for applied probabilists wishing to generalize beyond the exponential while retaining some of its key properties.The phase-type family includes the exponential,mixture of exponentials,Erlangian and Coxian distributions as special cases.

The phase-type distributions are very popular in risk theory.A large number of researchers have studied phase-type distributions on a variety of risk models.Feng[5]gave ruin-related quantities in the phase-type renewal risk model.Liet al.[6]consider the de ficit of ruin in a discrete-time Sparre Andersen model with phase-type claims.Stanfordet al.[7]estimated the finite-time ruin probabilities in the Sparre Andersen by phase-type approximations.Ng[8]gave the uncrossing and downcrossing probabilities of a dual risk model with phase-type gains.

Phase-type distributions were first introduced by Neuts[9]in 1975.A shortened treatment can be stated as follows.Consider a Markov process with transient states{1,2,···,m}and absorbing statem+1,whose in finitesimal generatorQhas the form

The diagonal entriesSiiare necessarily negative,other entries are non-negative,and

wheree′is anm×1 column vector of ones,represents the rates at which transitions occur from the individual transient states to the absorbing state.Let the process start in stateiwith probabilityai(i=1,2···,m,m+1),anda=(a1,a2,···,am)(in many practical problems,am+1=0).Under these assumptions,the timeVuntil absorption has occurred has distribution function

and density function

where the matrix exponential is de fi ned by

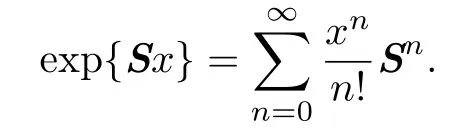
As this distribution is completely determined byaandS,we say either thatVhas a phasetype distribution with representation(a,S)of dimensionm,or write

Occasionally,we say thatVhas a phase-type(m)distribution.For a more detailed description of phase-type distributions,see[10].

Phase-type(2)distributions are phase-type distributions withm=2.The matrixScan be written

whereλ,µ＞0,0≤α,β≤1 andαβ＜1.

Lemma 2.1([11],Lemma 1)Any phase-type(2)distribution with parameters a and S, where S satis fies(2.1),is either a linear combination of two exponential densities,or a linear combination of an exponential and an Erlang(2)density with the same scale parameter.

By Lemma 2.1,we can see that when individual claim amountXi～PH2(a,S),its density function can be written as

3 The Laplace Transform of φ(u)

In this section,we consider the time and amount of the first claim,and obtain the Laplace transform ofφ(u),the explicit expression forφ(0),distribution function about the surplus prior to ruin and the de ficit at ruin.

Theorem 3.1Under above assumptions,we obtain

Proof. Considering the time and amount of the first claim and using the similar method in [12],we have

Taking the Laplace transform with respect touin(3.1),and noting thatτ(u)is a convolution,we obtain

IfI′(0)≥0,then the functionI(s)is increasing on(0,∞);ifI′(0)＜0,then the functionI(s)is decreasing up to some point,and it is increasing from this point on.So,in both cases the solution of(3.3)exists and it is unique.

By the above observation,the denominator in(3.2)is zero withs=s0.Hence the numerator in(3.2)must be zero withs=s0ass0φ∗(s0)＞0.We obtain

(this is the fi nal-value theorem of Laplace transform,see[13]).Thus we have

This completes the proof.

Remark 3.1Denote the ruin probability by

Remark 3.2Let

H(u,x,y)may be interpreted as probability that ruin occurs from initial surplusuwith the de ficit at ruin no greater thanyand the surplus prior to ruin no greater thanx(see [14]).Clearly,

whereh(u,x,y)is the joint density function of surplus prior to ruin and de ficit at ruin with initial surplusu,andh(0,x,y)with initial surplus 0.Using(3.7)–(3.9),we can get the expression of the joint density.

Remark 3.4Theoretically we can use Laplace inversion to get the expression ofφ(s)by Theorem 3.1.But it should be kept in mind that the inversion problem is difficult in some real cases(see[13,15]).

4 Example

In this section,we illustrate the application of the results of the previous section with an example.The results in this section can be readily obtained using packages such as Mathematica.

We assume that inter-claim timeWihas a phase-type distribution with representation (a,S)of dimension 2,where

the individual claim amountXihas density function

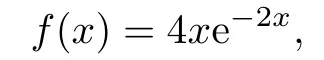
[1]Landriault D,Willmot G.On the Gerber-Shiu discounted penalty function in the Sparre Andersen model with an arbitrary interclaim time distribution.Insurance Math.Econom., 2008,42(2):600–608.

[2]Zhao X,Yin C.The Gerber-Shiu expected discounted penalty function for Lvy insurance risk processes.Acta Math.Appl.Sinica(English Ser.),2009,26(4):575–586.

[3]Cheung E C K,Landriault D,Willmot G E,Woo J K.Structural properties of Gerber-Shiu functions in dependent Sparre Andersen models.Insurance Math.Econom.,2010,46(1):117–126.

[4]Song M,Meng Q B,Wu R,Ren J D.The Gerber-Shiu discounted penalty function in the risk process with phase-type interclaim times.Appl.Math.Comput.,2010,216:523–531.

[5]Feng R.A matrix operator approach to the analysis of ruin-related quantities in the phase-type renewal risk model.Bull.Swiss Assoc.Actuaries,2009,1(2):71–87.

[6]Li S,Lu Y,Garrido J.A review of discrete-time risk models.Rev.R.Acad.Cien.Serie A. Mat.,2009,103(2):321–337.

[7]Stanford D,Avram F,Badescu A,Breuer L.Phase-type approximations to finite-time ruin probabilities in the Sparre Andersen and stationary renewal risk models.Astin Bull.,2005, 35(1):131–144.

[8]Ng A C Y.On the upcrossing and downcrossing probabilities of a dual risk model with phasetype gains.Astin Bull.,2010,40(1):281–306.

[9]Neuts M F.Matrix-geometric Solutions in Stochastic Models.Baltimore:John Hopkins Univ. Press,1981.

[10]Asmussen S.Ruin Probabilities.Singapore:World Scienti fi c,2000.

[11]Dickson D C M,Hipp C.Ruin problems for phase-type(2)risk processes.Scand.Actuar.J., 2000,46(1):147–167.

[12]Cheng Y,Tang Q.Moments of the surplus before ruin and the de ficit at ruin in the Erlang (2)risk process.N.Am.Actuar.J.,2003,7(1):1–12.

[13]Dickson D C M.On a class of renewal risk processes.N.Am.Actuar.J.,1998,2(3):60–73.

[14]Willmot G E,Dickson D C M.The Gerber-Shiu discounted penalty function in the stationary renewal risk model.Insurance Math.Econom.,2003,32(3):403–411.

[15]Gerber H U,Shiu E S W.On the time value of ruin.N.Am.Actuar.J.,1998,2(1):48–78.

Communicated by Wang De-hui

60P05,60H10

A

1674-5647(2012)04-0349-10

date:Sept.28,2010.

Tianyuan NSF(11126176)of China.