A Maschke Type Theorem for Doi-Hopf π-modules∗

CHEN QUAN-GUO AND TANG JIAN-GANG

(Department of Mathematics,Yili Normal University,Yining,Xinjiang,835000)

A Maschke Type Theorem for Doi-Hopfπ-modules∗

CHEN QUAN-GUO AND TANG JIAN-GANG

(Department of Mathematics,Yili Normal University,Yining,Xinjiang,835000)

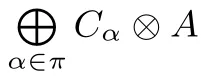
integral,Hopfπ-coalgebra,Hopf algebra,Maschke type theorem

1 Introduction

A clue result in classical representation theory is Maschke’s theorem,which states that a group ring over a finite group is semisimple if and only if the characteristic of the field does not divide the order of the group.Keeping in mind the fact that a group ring is an example of a Hopf algebra,one can ask if Maschke’s theorem can be generalized to finite-dimensional Hopf algebras.Larson and Sweedler[1]proved that a finite-dimensional Hopf algebra is semisimple if and only if there exists a left or right integral inH,such that the image of this integral under the augmentation map equals 1.If one works over a fixed fieldk,the semisimplicity is replaced by the following condition:every short exact sequence ofH-modules that splits as a sequence ofk-linear spaces,also splits as a sequence ofH-modules.

Several other generalizations of Maschke’s theorem have appeared in the literature.Doi[2]proved a Maschke type theorem for relative Hopf modules under some restrictive conditions which can be got rid of.Soon afterwards,a Maschke type theorem for Doi-Hopf modules was proved by Caenepeelet al.[3]Recently,Wang[4]generalized Maschke’s theorem to Hopfπ-comodules.A natural question occurs to us that whether Maschke’s theorem can be generalized to Doi-Hopfπ-modules.

The purpose of this paper is devoted to solving the question presented above,but we need to overcome the key question,i.e.,how to introduce the notion of integral map for Doi-Hopfπ-datum.In 2002,Menini and Militaru[5]de fi ned the more general concept of an integral associated to a three tuple(H,A,C)called the Doi-Koppinen datum,consisting of a Hopf algebraHwhich coacts on an algebraAand acts on a coalgebraC.Inspired by the idea in[5],we introduce the notion of integral map for Doi-Hopfπ-datum(see De fi nition 3.1).In the sequel,we present Maschke’s theorem for Doi-Hopfπ-modules.

This paper is organized as follows.In Section 2,we recall de fi nitions and basic results related to Hopf group-coalgebras which are needed later.In Section 3,the notions of integral are introduced,then we prove a Maschke type theorem for Doi-Hopfπ-modules(see Theorem 3.1),which applies to Doi-Hopf modules(see Corollary 3.1)and Hopfπ-comodules(see Corollary 3.2).Finally,we consider the application of the existence of the total integral(see Theorem 3.2).

2 Preliminaries

In this section,we recall de fi nitions and discuss properties of Hopf group-coalgebras and comodule algebras.Most of the materials presented here can be found in[4,6–12].

Throughout this paper,we always letπbe a finite discrete group with a neutral elementeandkbe a field.If a tensor product is written without index,then it is assumed to be taken overk,that is,⊗=⊗k.IfUandVarek-spaces,thenTU,V:U⊗V→V⊗Udenote the fl ip map de fi ned by

2.1 The π-coalgebras

Aπ-coalgebra is a family ofk-spaces

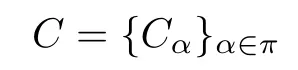
together with a family ofk-linear maps

(called a comultiplication)and ak-linear map

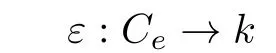
(called a counit)such that∆is coassociative in the sense that

Remark 2.1(Ce,∆e,e,ε)is an ordinary coalgebra in the sense of Sweedler.Following the Sweedler’s notation forπ-coalgebras,for anyα,β∈πandc∈Cαβ,we write

The coassociativity axiom gives that,for anyα,β,γ∈πandc∈Cαβγ,

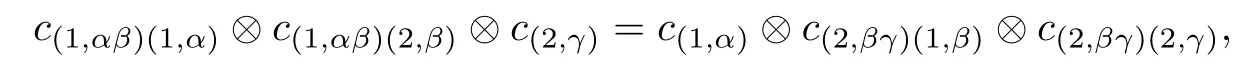
2.2 The Hopf π-coalgebras

A Hopfπ-coalgebra is aπ-coalgebra

together with a family ofk-linear maps

(called an antipode)such that the following data hold.EachHαis an algebra with multiplicationmαand unit 1α∈Hα,and for allα,β∈π,∆α,βandε:He→kare algebra maps, i.e.,for allc,c′∈Hαβ,

Note that the notion of a Hopfπ-coalgebra is not self-dual and(He,me,1e,∆e,e,ε,Se) is an ordinary Hopf algebra.A Hopfπ-coalgebraHis termed to be of finite type ifHαis finite-dimensional as ak-vector space for allα∈π.

2.3 The π-C-comodulelike Objects

Let

2.4 The π-H-comodule Algebras

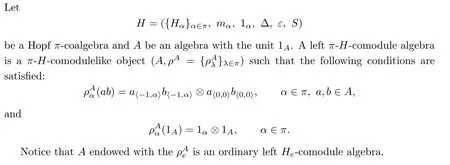
2.5 The Total Integrals

Let

be a Hopfπ-coalgebra andAbe a leftπ-H-comodule algebra.A family of maps

is called a total integral,ifφsatis fies the following conditions:

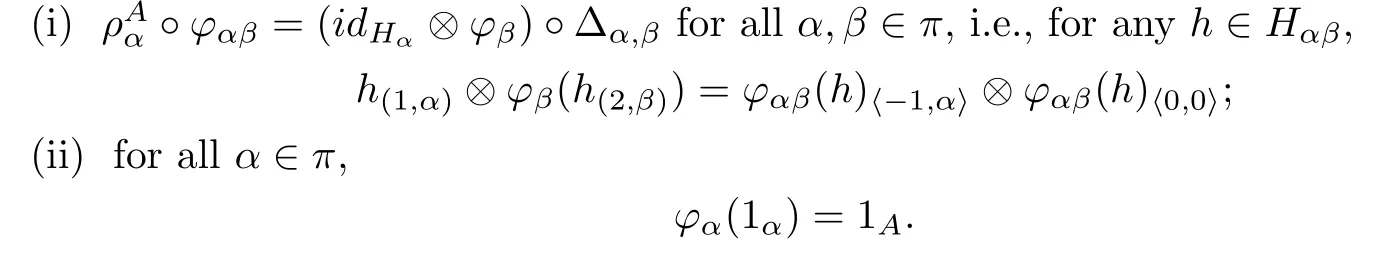
2.6 The π-H-module Coalgebras

Let

be a Hopfπ-coalgebra,and

be aπ-coalgebra.Cis called a rightπ-H-module coalgebra if there is a family ofk-linear maps

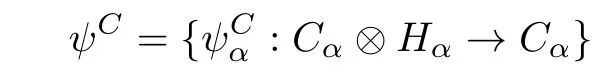
such that the following conditions are satis fi ed:

3 A Maschke Type Theorem

The set of Doi-Hopfπ-modules together with bothA-module maps andπ-C-comodule maps form a category of Doi-Hopfπ-modules and can be denoted byπ-CU(H)A(called a Doi-Hopfπ-modules category).

Remark 3.1(1)Ifπ={e},then the equations in De fi nition 3.1 are just the forms in [5].

(2)We point out that the integrals introduced above are in line with total integrals on Hopfπ-coalgebras.For this,letC=Hand

Proof.Sincevis a split injection inUA,there exists a morphismu:N→MinUAsuch

So the theorem is proved.

Now,we consider the application of the Theorem 3.1 to the following cases.Takeπ={e}. Then Hopfπ-coalgebras are just the ordinary Hopf algebras.The De fi nition 3.1 is restated as follows.Let(H,A,C)be a Doi-Hopf datum.A family ofk-linear mapθ:C→Hom(C,A) is called an integral of(H,A,C)if

An integralθ:C→Hom(C,A)is called total if

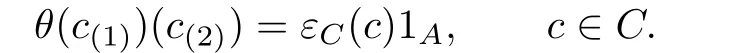
In addition,a total integralθ:C→Hom(C,A)is called anA-integral if the total integral satis fies theA-centralising condition

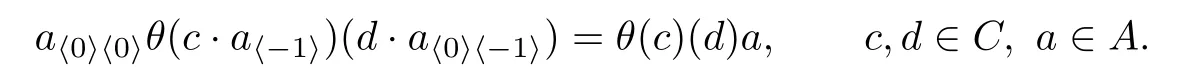
From the Theorem 3.1,we have the following conclusion.

Corollary 3.1[3]Let(H,A,C)be a Doi-Hopf datum,and there exists an A-integral θ:C→Hom(C,A).If M∈HU(H)Ais semisimple as a right A-module,then M is semisimple as an object inHU(H)A.

Let(H,A)be a Hopfπ-comodule.Then(H,A,H)is a Doi-Hopfπ-datum.Assume that there exists a total integral

As in Remark 3.1,we de fi ne

holds.Then an monomorphism f:M→N of(H,A)-Hopf modules splits if the monomorphism f splits as an A-module morphism.

Finally,we prove the main applications of the existence of a total integral.

Theorem 3.2Let(H,A,C)be a Doi-Hopf π-datum and suppose that there exists a total integral

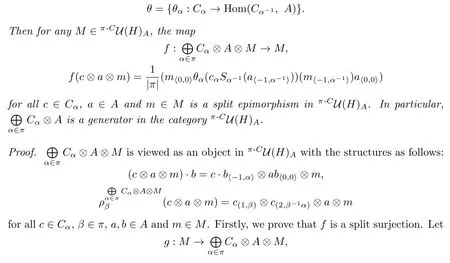
for allm∈M.Thengis leftπ-C-colinear(but is not rightA-linear),and form∈M,we have

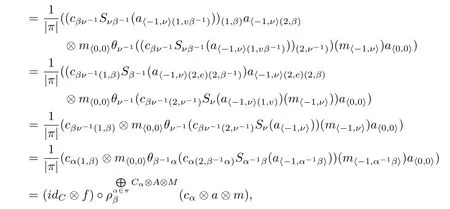
i.e.,fis leftπ-C-colinear.Hence,we have proved thatfis an epimorphism inπ-CU(H)Aand has aπ-C-colinear section.The proof of Theorem 3.2 is completed.

[1]Larson R G,Sweedler M E.An associative orthogonal bilinear form for Hopf algebras.Amer. J.Math.,1969,91:75–94.

[2]Doi Y.Hopf extensions of algebras and Maschke type theorems.Israel J.Math.,1990,72: 99–108.

[3]Caenepeel S,Militaru G,Zhu S L.A Maschke type theorem for Doi-Hopf modules and applications.J.Algebra,1997,187:388–412.

[4]Wang S H.A Maschke-type theorem for Hopfπ-comodules.Tsukuba J.Math.,2004,28:377–388.

[5]Menini C,Militaru G.Integral,quantum Galois extensions,and the affineness criterion for quantum Yetter-Drinfel’d modules.J.Algebra,2002,247:467–508.

[6]Zunino M.Double construction for crossed Hopf coalgebra.J.Algebra,2004,278:43–75.

[7]Zunino M.Yetter-Drinfeld modules for Turaev crossed structures.J.Pure Appl.Algebra,2004, 193:313–343.

[8]Virelizier A.Hopf group-coalgebras.J.Pure Appl.Algebra,2002,171:75–122.

[9]Wang S H.Group entwining structures and group coalgebra Galois extensions.Comm.Algebra, 2004,32:3417–3436.

[10]Wang S H.Group twisted smash products and Doi-Hopf modules for T-coalgebras.Comm. Algebra,2004,32:3437–3458.

[11]Wang S H.Morita contexts,π-Galois extensions for Hopfπ-coalgebras.Comm.Algebra,2006, 34:521–546.

[12]Turaev V G.Homotopy field theory in dimension 3 crosses group-categories.Preprint, GT/0005291.

Communicated by Du Xian-kun

16W30,16W50

A

1674-5647(2012)04-0289-11

date:Aug.31,2010.

The NSF(10871137)of China.