An Almost Sure Central Limit Theorem for Weighted Sums of Mixing Sequences∗

ZOU GUANG-YUAND ZHANG YONG

(1.Institute of Mathematics,Jilin University,Changchun,130012)

(2.School of Science,Changchun Institute of Technology,Changchun,130012)

An Almost Sure Central Limit Theorem for Weighted Sums of Mixing Sequences∗

ZOU GUANG-YU1,2AND ZHANG YONG1

(1.Institute of Mathematics,Jilin University,Changchun,130012)

(2.School of Science,Changchun Institute of Technology,Changchun,130012)

In this paper,we prove an almost sure central limit theorem for weighted sums of mixing sequences of random variables without stationary assumptions.We no longer restrict to logarithmic averages,but allow rather arbitrary weight sequences. This extends the earlier work on mixing random variables.

almost sure central limit theorem,weighted sum,mixing sequence, logarithmic average

1 Introduction and Main Results

The almost sure central limit theorem(ASCLT)was first introduced independently by Brosamler[1]and Schatte[2].Since then many interesting results have been discovered in this field.Let{Xn,n≥1}be a sequence of i.i.d.random variables with

Here and in the sequel,logn=ln(n∨e),I{·}denotes indicator function andΦ(·)is the distribution function of the standard normal random variable.The above ASCLT is said to be hold with logarithmic averages.Many interesting results have been obtained in this field (see[3–11]).

Many useful linear statistics based on a random sample are weighted sums of random variables.Examples include least-square estimators,nonparametric regression function es-timators and jackknife estimates,among others.Therefore,studies of the limit properties for these weighted sums have been demonstrated to be a signi fi cant process in probability theory with applications in mathematical statistics.Up to now,various limit properties such as central limit theorem,law of large number,complete convergence and so on,have been studied by many authors.Zhanget al.[8]obtained the ASCLT for weighted sums under association with logarithmic averages.But few results about ASCLT for weighted sums under mixing sequences have been studied.From Zhanget al.[9],Gonchigdanzan and Rempala[12], Li and Wang[13],we know that the proof of the ASCLT for weighted sums is an important step in the proof of the ASCLT for products of sums.

At first,we recall some measures of dependence between two algebras.

De fi nition 1.1Let A and B be two σ-algebras of events.We de fi ne

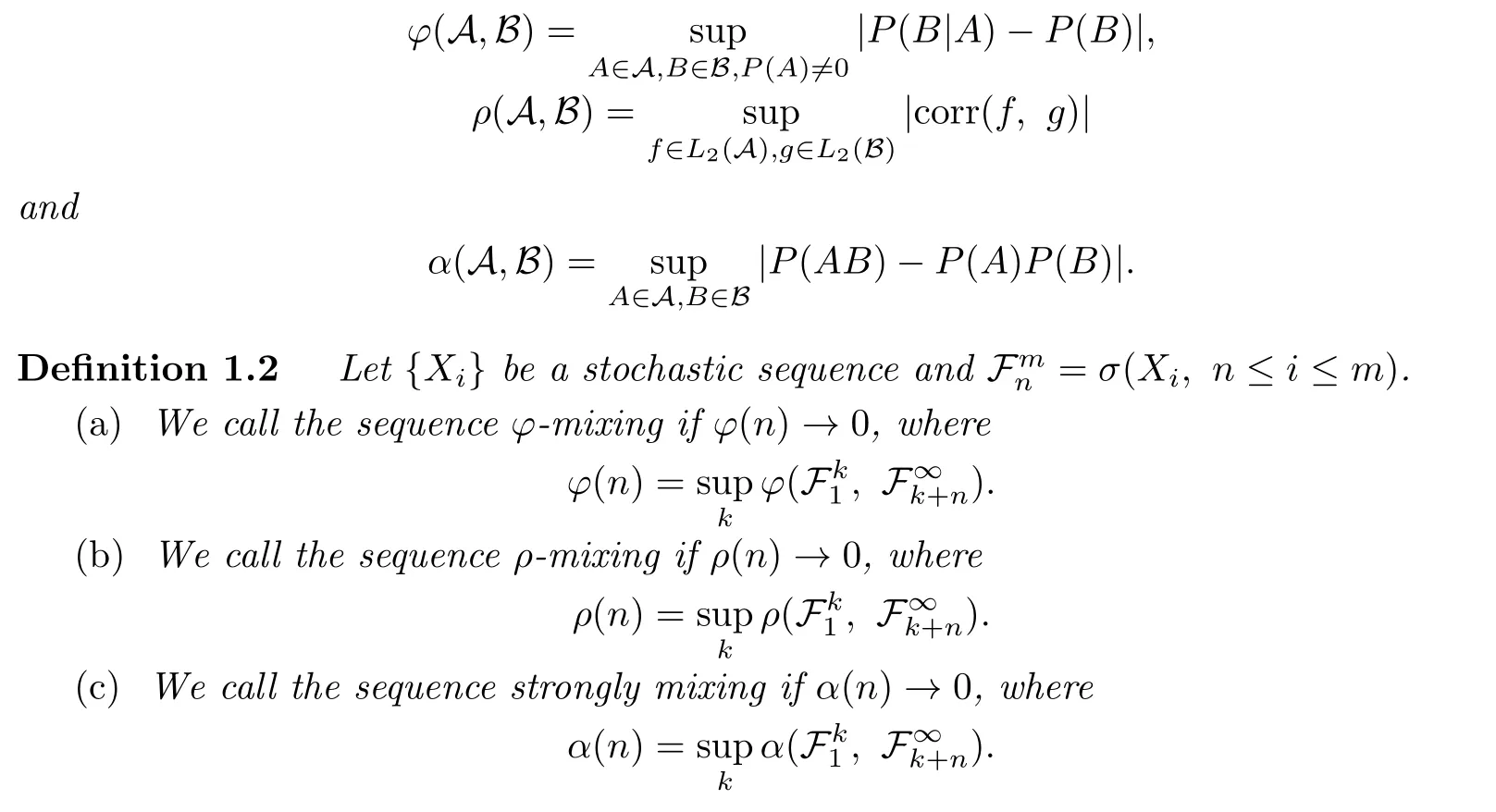
It is well known that theφ-mixing condition is the most restrictive and the strong mixing is the weakly among all(see[14]for a survey).In this paper,we study the ASCLT of weighted sums for these three classes of dependent random variables.Our theorem extends the known results for strictly mixing sequence from equal weights to general weights,weakening at the same time the assumption of stationary.And also we extend the ASCLT with other sequence{Dn,n≥1}tending faster to in fi nity than the logarithmic averages.The following theorem is our main result.

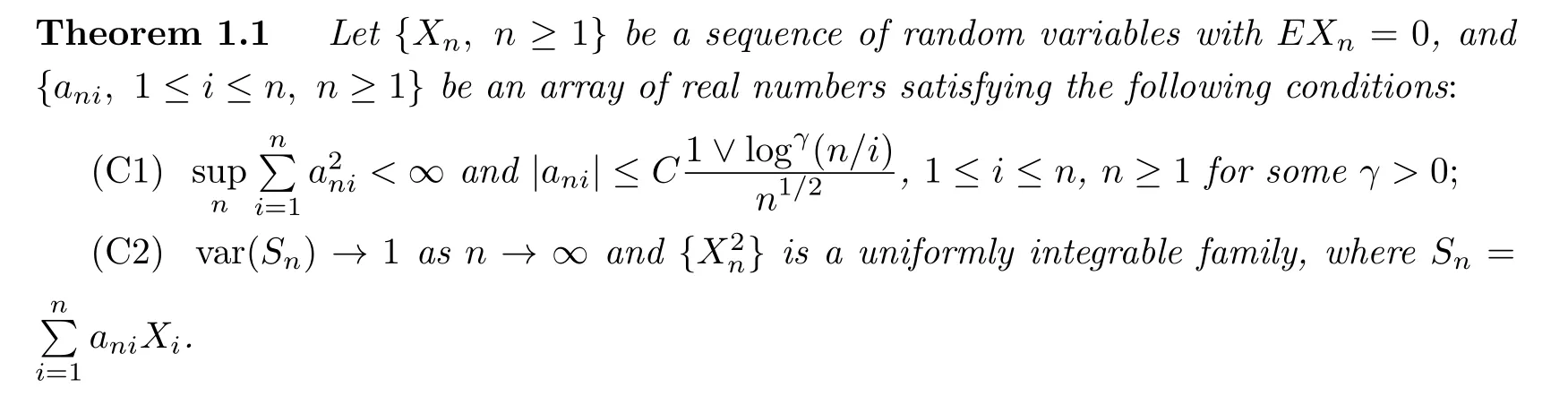
2 Some Lemmas

The proof of Theorem 1.1 is based on the following lemmas.

3 Proof of Theorem 1.1

Letfbe a bounded Lipschitz function and have a Radon-Nikodyn derivativef′bounded byΓ.From(3.1),we have

The proofs of Theorem 1.1 under the assumptions(a)and(b)are similar to the proof under the assumption(c),so we omit it here.

[1]Brosamler G A.An almost everywhere central limit theorem.Math.Proc.Cambridge Philos. Soc.,1988,104:561–574.

[2]Schatte P.On strong versions of the central limit theorem.Math.Nachr.,1988,137:249–256.

[3]Berkes I,Cs`aki E.A universal result in almost sure central limit theory.Stochastic Process. Appl.,2001,94:105–134.

[4]Gonchigdanzan K.Almost sure central limit theorems for strongly mixing and associated random variables.Internat.J.Math.Math.Sci.,2002,29(3):125–131.

[5]Wang F,Cheng S H.Almost sure central limit theorems for heavily trimmed sums,Acta Math. Sinica(English Ed.),2004,20:869–878.

[6]Lu C R,Qiu J,Xu J J.Almost sure central limit theorems for random functions,Sci.China Ser.A,2006,49:1788–1799.

[7]Fredrik J.Almost Sure Central Limit Theory.Uppsala:Uppsala University,Department of Mathematics,2007.

[8]Zhang Y,Dong Z S,Zhao S S.An almost sure central limit theorem for weighted sums under association.Acta Math.Sci.(Chinese),2009,29(6):1487–1491.

[9]Zhang Y,Yang X Y,Dong Z S.An almost sure central limit theorem for products of sums of partial sums under association.J.Math.Anal.Appl.,2009,355:708–716.

[10]Huang S H,Pang T X.An almost sure central limit theorem for self-normalized partial sums.Comput.Math.Appl.,2010,60:2639–2644.

[11]Zhang Y,Yang X Y.An almost sure central limit theorem for self-normalized products of sums of i.i.d.random variables.J.Math.Anal.Appl.,2011,376:29–41.

[12]Gonchigdanzan K,Rempala G.A note on the almost sure limit theorem for the product of partial sums.Appl.Math.Lett.,2006,19:191–196.

[13]Li Y X,Wang J F.An almost sure central limit theorem for products of sums under association.Statist.Probab.Lett.,2008,78:367–375.

[14]Bradley R C.Basic Properties of Strong Mixing Conditions.In:Eberlein E,Taqqu M S. Dependence in Probability and Statistics.Boston:Birkh auser,1986:165–192.

[15]Peligrad M,Shao Q M.A note on the almost sure central limit theorem for weakly dependent random variables.Statist.Probab.Lett.,1995,22:131–136.

[16]Lin Z Y,Lu C R.Limit Theory for Mixing Dependent Random Variables.Beijing:Science Press,1996.

[17]Peligrad M,Utev S.Central limit theorem for linear process.Ann.Probab.,1997,25,443–456.

[18]Lacey M T,Philipp W.A note on the almost sure central limit theorem.Statist.Probab.Lett., 1990,9:201–205.

[19]Billingsley P.Convergence of Probability Measures,New York:Wiley,1968.

Communicated by Wang De-hui

60F15,60F05

A

1674-5647(2012)04-0359-08

date:Oct.31,2011.

The NSF(11101108)of China.