Extinction of Weak Solutions for Nonlinear Parabolic Equations with Nonstandard Growth Conditions∗

GAO JING-LU AND GUO BIN

(School of Mathematics,Jilin University,Changchun,130012)

Extinction of Weak Solutions for Nonlinear Parabolic Equations with Nonstandard Growth Conditions∗

GAO JING-LU AND GUO BIN

(School of Mathematics,Jilin University,Changchun,130012)

This paper deals with the extinction of weak solutions of the initial and boundary value problem forut=div((|u|σ+d0)|∇u|p(x)−2∇u).When the exponent belongs to different intervals,the solution has different singularity(vanishing in finite time).

nonlinear parabolic equation,nonstandard growth condition,p(x)-Laplacian operator

1 Introduction

LetΩ⊂RN(N>2)be a bounded Lipschitz domain and 0＜T＜∞.Consider the following general quasilinear degenerate parabolic problem:

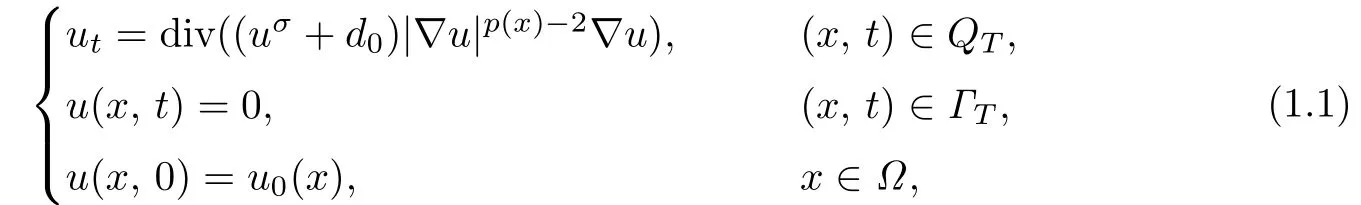
whereQT=Ω×(0,T]andΓTdenotes the lateral boundary of the cylinderQT.

Assume throughout the paper that the exponentp(x)is continuous in¯Ωwith logarithmic module of continuity:

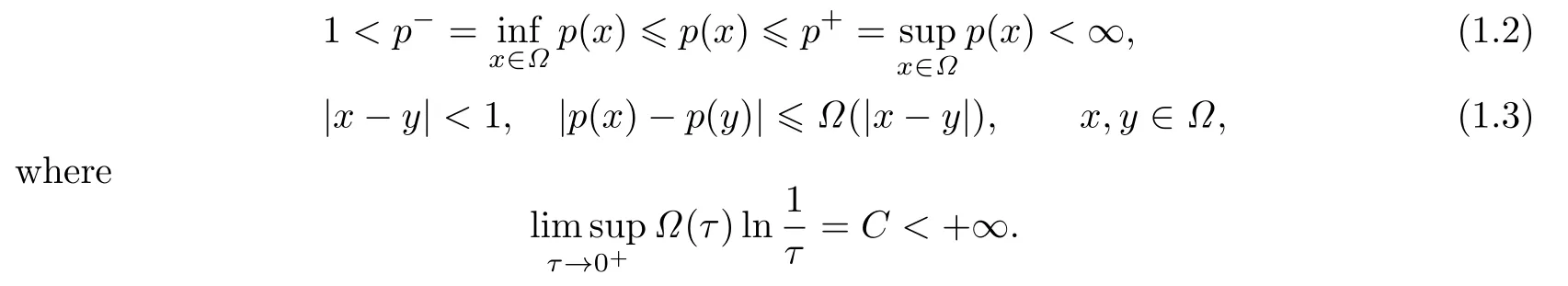
The model(1.1)proposed by Ruˆziˇcka[1]describe some properties of electro-rheological fl uids which change their mechanical properties dramatically when an external electric field is applied.The variable exponentpin the model(1.1)is a function of the external electric field|E|2which is subject to the quasi-static Maxwell’s equations

whereε0is the dielectric constant in vacuum and the electric polarizationPis linear inE,i.e.,P=λE.For more physical backgrounds,the interested readers may refer to[2–4]. These models include parabolic or elliptic equations which are nonlinear with respect to gradient of the thought solution and with variable exponents of nonlinearity(see[5–8]and references therein).Besides,another important application is the image processing where the anisotropy and nonlinearity of the di ff usion operator and convection terms are used to underline the borders of the distorted image and to eliminate the noise(see[9–11]).

In the case whenpis a fixed constant,Yin and Jin[12]discussed the extinction and non-extinction of solutions by applying comparison theorem and energy estimate methods. However,we point out that these methods used in[12]fail in our problems.The main reason is that the following identities do not hold

For many results about the existence,uniqueness,nonexistence and the properties of the solutions,we refer the readers to the bibliography given in[13–19].

To the best of our knowledge,there are only a few works about parabolic equations with variable exponents of nonlinearity.Applying Galerkin’s method,Antontsev and Shmarev[4]obtained the existence and uniqueness of weak solutions with the assumption that the functiona(u)in div(a(u)|∇u|p(x)−2∇u)is bounded.In the case when the functiona(u) in div(a(u)|∇u|p(x)−2∇u)might be not upper bounded,Guo and Gao[20−21]applied the method of parabolic regularization and Galerkin’s method to prove the existence of weak solutions.In this paper,we find when the exponent belongs to different intervals,the solution represents different singularity(vanishing in finite time).That is,

The outline of this paper is as follows:In Section 2,we introduce the function spaces of Orlicz-Sobolev type,and give the de fi nition of the weak solution to the problem.Section 3 is devoted to the proof of the extinction of the solution obtained in Section 2.

2 Preliminaries

We state some properties of variable exponent spaces and give the de fi nition of the weak solution to the problem.Let us first introduce the Banach spaces

and denote byW′(QT)the dual ofW(QT)with respect to the inner product inL2(QT).

For the sake of simplicity,we first state some results about the properties of the Luxemburg norm.

Lemma 2.1[22−23]For any u∈Lp(x)(Ω),

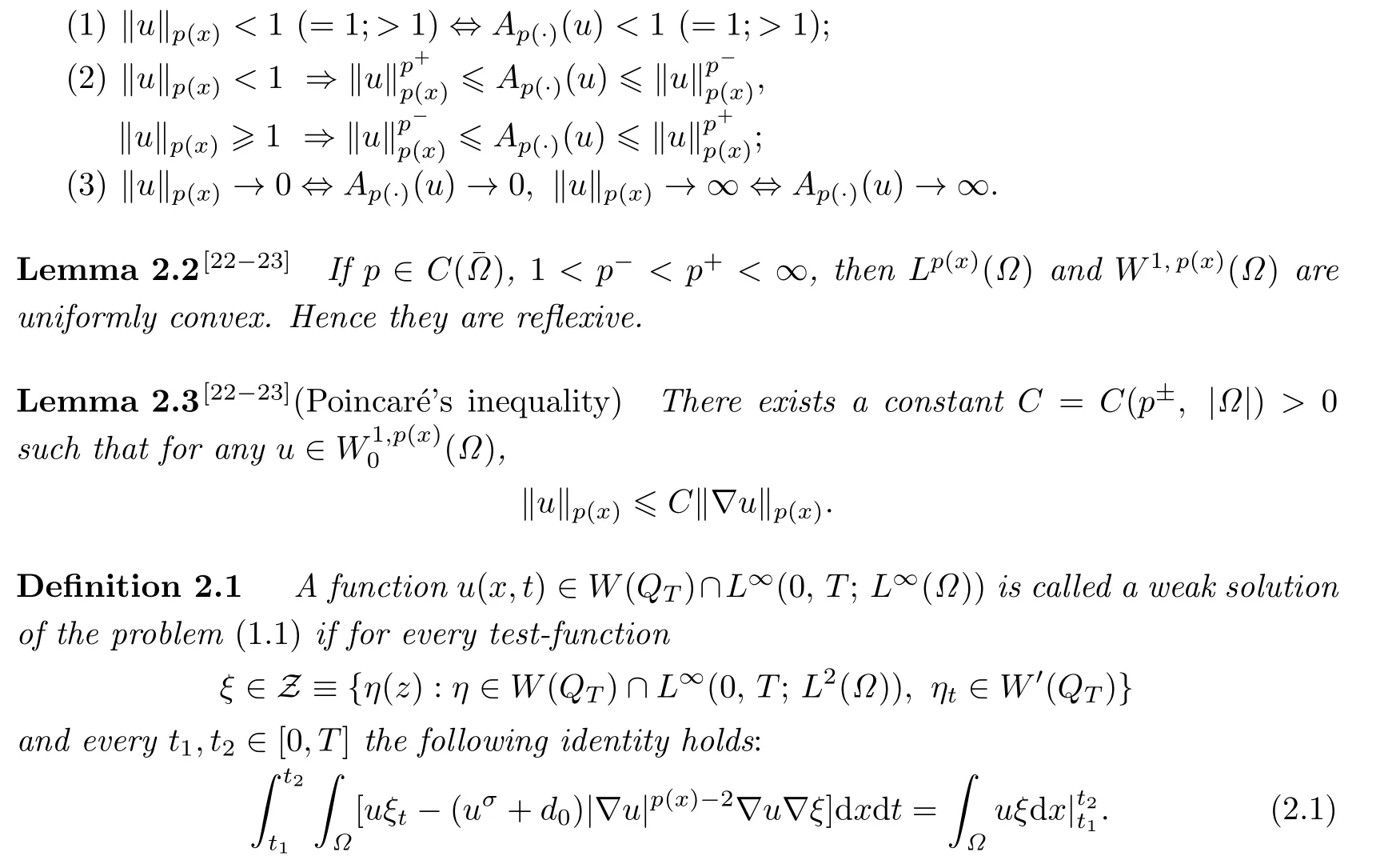
3 Main Results and Their Proofs

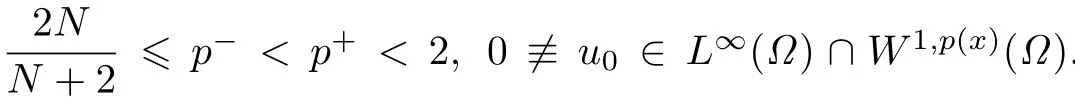
[1]Ruzicka M.Electrorheological Fluids:Modelling and Mathematical Theory.Lecture Notes in Math.1748.Berlin:Springer,2000.

[2]Acerbi E,Mingione G.Regularity results for stationary electrorheological fl uids.Arch.Rational Mech.Anal.,2002,164:213–259.

[3]Acerbi E,Mingione G,Seregin G A.Regularity results for parabolic systems related to a class of non Newtonian fl uids.Anna.Inst.H.Poincare Anal.Non Lineaire,2004,21:25–60.

[4]Acerbi E,Mingione G.Regularity results for a class of functionals with nonstandard growth.Arch.Rational.Mech.Anal.,2001,156(1):121–140.

[5]Antontsev S N,Shmarev S I.Anisotropic parabolic equations with variable nonlinearity.Publ. Mat.,2009,53:355–399.

[6]Antontsev S N,Shmarev S I.Parabolic equations with anisotropic nonstandard growth conditions.Internat.Ser.Numer.Math.,2007,154:33–44.

[7]Antontsev S N,Zhikov V.Higher interability for parabolic equations ofp(x,t)-Laplacian type.Adv.Di ff erence Equations,2005,10:1053–1080.

[8]Lian S Z,Gao W J,Cao C L,Yuan H J.Study of the solutions to a model porous medium equation with variable exponents of nonlinearity.J.Math.Anal.Appl.,2008,342:27–38.

[9]Andreu-Vaillo F,Caselles V,Mazn J M.Parabolic Quasilinear Equations Minimizing Linear Growth Functions.vol.223.Progress in Mathematics.Basel:Birkhuser Verlag,2004.

[10]Aboulaich R,Meskine D,Souissi A.New di ff usion models in image processing.Comput.Math. Appl.,2008,56:874–882.

[11]Chen Y,Levine S,Rao M.Variable exponent,linear growth functionals in image restoration.SIAM J.Appl.Math.,2006,66:1383–1406.

[12]Yin J X,Jin C H.Critical extinction and blow-up exponents for fast di ff usivep-Laplacian with sources.Math.Methods Appl.Sci.,2007,30:1147–1167.

[13]Barret J,Liu W.Finite element approximation of the parabolicp-Laplacian.SIAM J.Numer. Anal.,1994,31:413–428.

[14]Dibenedetto E.Degenerate Parabolic Equations.New York:Springer-Verlag,1993.

[15]Erdem D.Blow-up of solutions to quasilinear parabolic equations.Appl.Math.Lett.,1999,12: 65–69.

[16]Kalashnikov A S.Some problems of the qualitative theory of nonlinear degenerate second-order parabolic equations.Russian.Math.Surveys,1987,42(2):169–222.

[17]Zhao J N.Existence and nonexistence of solutions forut=div(|∇u|p−2∇u)+f(∇u,u,x,t).J.Math.Anal.Appl.,1993,172:130–146.

[18]Levine H A.Some nonexistence and instability theorems for solutions of formally parabolic equations of the formPut=−Au+F(u).Arch.Ratioal Mech.Anal.,1973,51:371–386.

[19]Levine H A,Payne L E.Nonexistence of global weak solutions for classes of nonlinear wave and parabolic equations.J.Math.Anal.Appl.,1976,55:329–334.

[20]Guo B,Gao W J.Study of weak solutions for parabolic equations with nonstandard growth conditions.J.Math.Anal.Appl.,2011,374(2):374–384.

[21]Guo B,Gao W J.Existence and asymptotic behavior of solutions for nonlinear parabolic equations with variable exponent of nonlinearity.Acta Math.Sci.,2012,32(3):1053–1062.

[22]Fan X L,Zhang Q H.Existence of solutions forp(x)-Laplacian Dirichlet problem.Nonlinear Anal.,2003,52:1843–1852.

Communicated by Gao Wen-jie

35K35,35K65,35B40

A

1674-5647(2012)04-0376-07

date:June 16,2012.

Partially supported by the NSF(11271154)of China and the 985 program of Jilin University.