The Existence of Three Positive Solutions for p-Laplacian Di ff erence Equation with Delay∗

WANG LIN-JUNAND GONG CHENG-CHUN

(1.Faculty of Science,Jiangsu University,Zhenjiang,Jiangsu,212013)

(2.School of Mathematics,Jilin University,Changchun,130012)

The Existence of Three Positive Solutions forp-Laplacian Di ff erence Equation with Delay∗

WANG LIN-JUN1,2AND GONG CHENG-CHUN2

(1.Faculty of Science,Jiangsu University,Zhenjiang,Jiangsu,212013)

(2.School of Mathematics,Jilin University,Changchun,130012)

In this paper,we study the multiplicity of positive solutions for a class ofp-Laplacian di ff erence equations with delay.We propose sufficient conditions for the existence of at least three positive solutions and we also provide two numerical examples to illustrate the theoretical results.

p-Laplacian,di ff erence equation,delay, fixed point theorem

1 Introduction

Thep-Laplacian differential equations have been vastly applied in many fields such as non-Newtonian mechanics,economics,neural networks,ecology,nonlinear flow laws,etc.(see [1–5]).

One of the important examples was described in[6].Letx=(x1,x2)be the two Cartesian coordinates in the plane of the glacier occupying a Lipschitzian domainΩ.We denote byu(x)the horizontal velocity component of the ice at the pointx.After a rescaling of the physical velocity of the ice,usatis fies the equation

whereeis a hydrostatic pressure force acting on the glacier andψis a function resulting from a constitutive law for the ice.The typical case of(1.1)is the following equation:

whereφp(s)=|s|p−2swithp＞1 andB(0,Ri)⊂Rdare the open balls centred about the origin with radiusRi,respectively.People are interested in considering positive radial solutions of the equation(1.2).Then(1.2)can be reduced to the following form(see[7]):

The equation(1.5)is a typical type of one-dimensionalp-Laplacian equation.

In the real world,some processes are more reasonably described asp-Laplacian differential equations with delay(see[2,8–9]).The reason is that the differential of the unknown solutions depends not only on the values of the unknown solutions at the current time,but also on the values prior to that.Such equations,to a certain extent,re fl ect much more exactly the physical reality than the equations without delay.

In recent years,p-Laplacian differential equations with delay have received a lot of attention(see[8–9]).There exists a large number of papers devoted to study the existence of positive solutions for such problems(see[1–2],[8–9]).

In reality,the equation(1.5)is applied together with some boundary value conditions. We can apply the standard Euler method to discretize the equation(1.5)and approximate its solutions numerically.An immediate and natural question is if the corresponding di ff erence equation together with boundary conditions has positive solutions.

In this paper,we are concerned with the followingp-Laplacian di ff erence equation with delay.We prove the multiplicity of positive solutions for the following system of equations:

Recently,the existence of positive solutions forp-Laplacian di ff erence equations with different types of boundary value conditions is investigated in[3,10–15]and the references therein.

By using Guo-Krasnoselskii fixed point theorem and a fixed point index theorem,He[16]proved the existence of one or two positive solutions for the following system ofp-Laplacian di ff erence equations:

Based on a fixed point theorem due to Avery and Henderson,Li and Lu[17]obtained at least two positive solutions for the problem(1.8)-(1.9).Wang and Guan[18]proved that the problem(1.8)-(1.9)has at least three positive solutions by using the Five Functionals Fixed Point Theorem.

Avery and Peterson[19],using a fixed point theorem,studied the existence of multiple positive solutions for the following system of di ff erence equations with delay:

Liu[20]established sufficient conditions for the existence of at least one solution for the following system of second-order nonlinear di ff erence equations with delay:

subject to the boundary value conditions

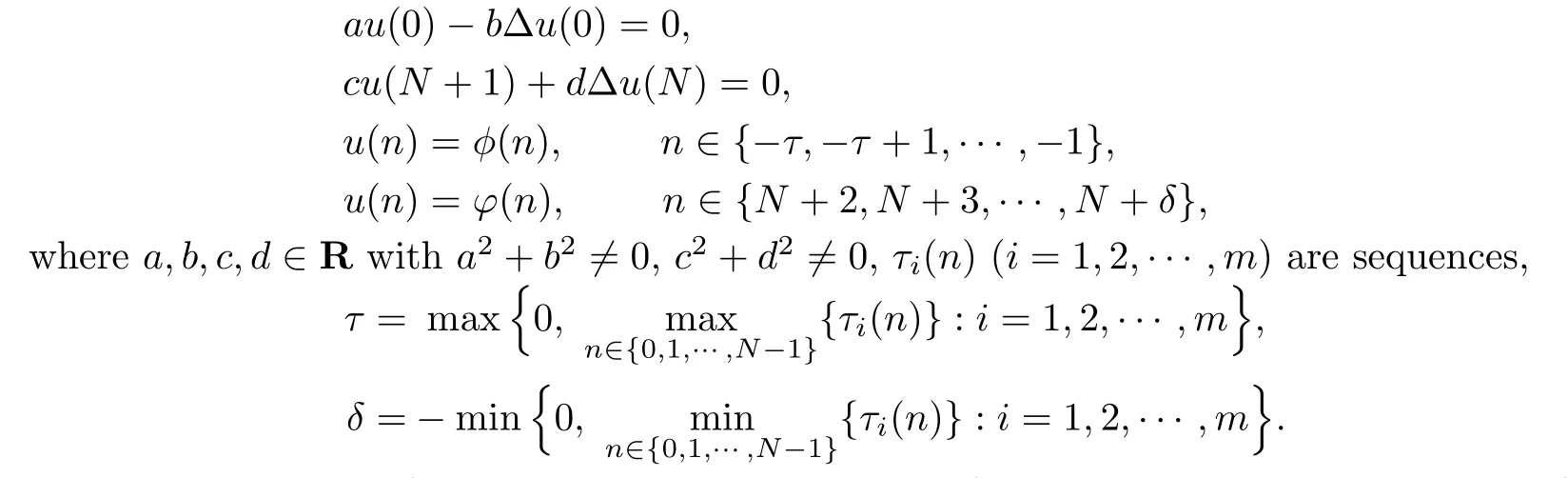
In this paper,we focus on proving the existence of at least three positive solutions for the system of equations(1.6)with the boundary condition(1.7).

This paper is organized as follows.In Section 2,we introduce some basic de fi nitions and state the Five Functionals Fixed Point Theorem.In Section 3,by applying the Five Functionals Fixed Point Theorem,we prove that the problem(1.6)-(1.7)has at least three positive solutions.In Section 4,we present two numerical examples to illustrate the theoretical results.

2 Preliminaries

In this section,we introduce some basic de fi nitions and recall the Five Functionals Fixed Point Theorem which plays a fundamental role in our subsequent analysis.

De fi nition 2.1Let E be a real Banach space.A nonempty closed convex set P⊂E is called a cone if

(i)x∈P and λ≥0imply λx∈P;

(ii)x∈P and−x∈P imply x=0.

De fi nition 2.2A map α:P→[0,∞)is said to be a nonnegative,continuous,concave functional on a cone P if it is continuous and satis fies

Similarly,a map β:P→[0,∞)is said to be a nonnegative,continuous,convex functional on a cone P if it is continuous and satis fies

Letα,ψbe nonnegative,continuous,concave functionals onPandγ,β,θbe nonnegative, continuous,convex functionals onP.For nonnegative real numbersa,b,c,handk,de fi ne the following convex sets:

The following Five Functionals Fixed Point Theorem is a fundamental principle in the proofs of our main results.

Theorem 2.1([21],Theorem 5)Let P be a cone in a real Banach space E.Suppose that there exist positive numbers c and M,nonnegative,continuous,concave functionals α and ψ on P,and nonnegative,continuous,convex functionals γ,β and θ on P,with α(x)≤β(x)andSuppose thatis completelycontinuous,and there exist nonnegative numbers h,k,a and b with0＜a＜b such that

(i){x∈P(γ,θ,α,b,k,c):α(x)＞b}/=∅and α(Tx)＞b for x∈P(γ,θ,α,b,k,c);

(ii){x∈Q(γ,β,ψ,h,a,c):β(x)＜a}/=∅and β(Tx)＜a for x∈P(γ,β,ψ,h,a,c);

(iii)α(Tx)＞b for x∈P(γ,α,b,c)with θ(Tx)＞k;

(iv)β(Tx)＜a for x∈Q(γ,β,a,c)with ψ(Tx)＜h.

Then T possesses at least three fixed pointssuch that β(x1)＜a,b＜α(x2),a＜β(x3)and α(x3)＜b.

3 Existence of Three Positive Solutions

In this section,we study the existence of three positive solutions for the following system of equations with delay:

We assume that:

(A1)f:{1,2,···,N+1}×R→R+is a continuous function,whereR+denotes the set of nonnegative reals;

(A2)a(·)is a positive function de fi ned on{1,2,···,N+1}.

For convenience,we first collect some properties of the functionφp(·).

Therefore,solving the problem(3.1)-(3.2)is equivalent to solving the equation(3.5). In the following,we de fi ne a map in terms of the equation(3.5)on an appropriate space, and then we study the fixed points of the corresponding map,which provides existence of solutions of the equation(3.5).

According to the assumptions(A1)and(A2),the mapT:E→Eis continuous.

Lemma 3.2Assume(A1)and(A2).Then T(P)⊂P.

Proof.For anyu∈P,from the de fi nition(3.6)we know that(Tu)(n)is increasing inn. Thus,

For anyn∈{0,1,···,N−1},direct computation shows that

According to Lemma 2 in[22],we haveU(n)≥0 for alln∈{0,1,···,N+1},which implies

This completes the proof.

We investigate the positive solutions of the problem(3.1)-(3.2)by searching for fixed points of the mapTon the coneP.

Lemma 3.3Assume that(A1)and(A2)hold.If u∈P,there holds

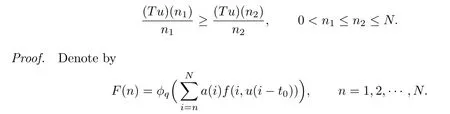
Then the functionF(n)is decreasing inn.Direct computation shows that

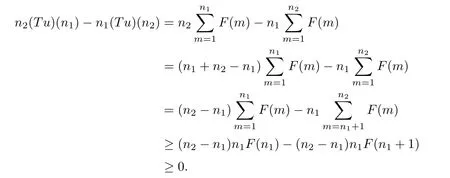
This completes the proof.

Letη,lbe fixed integers such that 0＜η＜l＜N+1−t0.Then we respectively de fi ne two nonnegative,continuous,concave functionalsα,ψonPand three nonnegative

Remark 3.1Obviously,this result applies to the case with delay itemt0=0.

4 Numerical Illustration

In this section,we present two numerical experiments to illustrate Theorem 2.1.

Example 4.1Consider the following equation witht0=2,N=4:

Then applying Theorem 3.1,we see that the problem(4.1)-(4.2)has at least three positive solutionsu1,u2andu3.

Numerically,we obtain three different positive solutions which are listed in Table 4.1.

Table 4.1 Three positive solutions for Example 4.1

It is easy to seeβ(u1)=u1(2)=0.2896＜1=a,α(u2)=u2(2)=16.8208＞3=b,β(u3)=u3(2)=2.7772＞1=aandα(u3)=u3(2)=2.7772＜3=b.

Example 4.2Consider the following equation witht0=2,N=100:

Then applying Theorem 3.1,we see that the problem(4.4)-(4.5)has at least three positive solutionsu1,u2andu3.

Numerically,we obtain three different solutions of the problem(4.4)-(4.5),which are shown in Fig.4.1.

Fig.4.1 Three different solutions of Example 4.2.

Similarly,computations giveβ(u1)=u1(51)=198.78＜200=a,α(u2)=u2(51)= 425.30＞400=b,β(u3)=u3(51)=230.46＞200=aandα(u3)=u3(51)=230.46＜400=b.

[1]Jiang D Q,Chu J F,O’Regan D,Agarwal R P.Positive solutions for continuous and discrete boundary value problems to the one-dimensionp-Laplacian.Math.Inequal.Appl.,2004,7: 523–534.

[2]Li W T,Huo H F.Positive periodic solutions of delay di ff erence equations and applications in population dynamics.J.Comput.Appl.Math.,2005,176:357–369.

[3]Liu Y J.A study on periodic solutions of higher order nonlinear functional di ff erence equations withp-Laplacian.J.Di ff erence Equations Appl.,2007,13:1105–1114.

[4]Feng H Y,Ge W G,Jiang M.Multiple positive solutions form-point boundary-value problems with a one-dimensionalp-Laplacian.Nonlinear Anal.,2008,68:2269–2279.

[5]Kim C G.Existence of positive solutions for singular boundary value problems involving the one-dimensionalp-Laplacian.Nonlinear Anal.,2009,70:4259–4267.

[6]Glowinski R,Rappaz J.Approximation of a nonlinear elliptic problem arising in a non-Newtonian fl uid flow model in glaciology.M2AN Math.Model.Numer.Anal.,2003,37:175–186.

[7]Jin C H,Yin J X,Wang Z J.Positive radial solutions ofp-Laplacian equation with sign changing nonlinear sources.Math.Methods Appl.Sci.,2007,30:1–14.

[8]Bai D Y,Xu Y T.Existence of positive solutions for boundary-value problems of second-order delay differential equations.Appl.Math.Lett.,2005,18:621–630.

[9]Jin C H,Yin J X.Positive solutions for the boundary value problems of one-dimensionalp-Laplacian with delay.J.Math.Anal.Appl.,2007,330:1238–1248.

[10]Agarwal R P.Di ff erence Equations and Inequalities.In:Monogr.Textbooks Pure Appl.Math. vol.155.New York:Marcel Dekker Inc.,1992.

[11]Agarwal R P,Wong Patricia J Y.Advanced Topics in Di ff erence Equations.In:Math.Appl. vol.404.Dordrecht:Kluwer Academic Publishers Group,1997.

[12]Liu Y J,Ge W G.Twin positive solutions of boundary value problems for finite di ff erence equations withp-Laplacian operator.J.Math.Anal.Appl.,2003,278:551–561.

[13]Jiang D Q,Zhang L L,O’Regan D,Agarwal R P.Existence theory for single and multiple solutions to singular positone discrete Dirichlet boundary value problems to the one-dimensionp-Laplacian.Arch.Math.(Brno),2004,40:367–381.

[14]He Z M.Double positive solutions of three-point boundary value problems forp-Laplacian di ff erence equations.Z.Anal.Anwendungen,2005,24:305–315.

[15]Liu Y J.Positive solutions of multi-point BVPs for second orderp-Laplacian di ff erence equations.Comm.Math.Anal.,2008,4:58–77.

[16]He Z M.On the existence of positive solutions ofp-Laplacian di ff erence equations.J.Comput. Appl.Math.,2003,161:193–201.

[17]Li Y K,Lu L H.Existence of positive solutions ofp-Laplacian di ff erence equations.Appl.Math. Lett.,2006,19:1019–1023.

[18]Wang D B,Guan W.Three positive solutions of boundary value problems forp-Laplacian di ff erence equations.Comput.Math.Appl.,2008,55:1943–1949.

[19]Avery R I,Peterson A C.Multiple positive solutions of a discrete second order conjugate problem.Panamer.Math.J.,1998,8:1–12.

[20]Liu Y J.On Sturm-Liouville boundary value problems for second-order nonlinear functional finite di ff erence equations.J.Comput.Appl.Math.,2008,216:523–533.

[21]Avery R I,Henderson J.Existence of three positive pseudo-symmetric solutions for a onedimensionalp-Laplacian.J.Math.Anal.Appl.,2003,277:395–404.

[22]Eloe P W.A generalization of concavity for finite di ff erences.Comput.Math.Appl.,1998,36: 109–113.

Communicated by Ma Fu-ming

39A10,34B18,34K28

A

1674-5647(2012)04-0337-12

date:Oct.9,2010.

The NSF(11071102)of China,the Research Fund(10JDG124)for High-level Group of Jiangsu University,and the NSF(11KJD110001)for Colleges and Universities in Jiangsu Province.