The Existence of Coupled Solutions for a Kind of Nonlinear Operator Equations in Partial Ordered Linear Topology Space∗

WU YUE-XIANG,HUO YAN-MEIAND WU YA-KUN

(1.College of Applied Mathematics,Shanxi University of Finance and Economics,

Taiyuan,030006)

(2.College of Economics,Shanxi University of Finance and Economics,Taiyuan,030006)

The Existence of Coupled Solutions for a Kind of Nonlinear Operator Equations in Partial Ordered Linear Topology Space∗

WU YUE-XIANG1,HUO YAN-MEI2AND WU YA-KUN1

(1.College of Applied Mathematics,Shanxi University of Finance and Economics,

Taiyuan,030006)

(2.College of Economics,Shanxi University of Finance and Economics,Taiyuan,030006)

The main purpose of this paper is to examine the existence of coupled solutions and coupled minimal-maximal solutions for a kind of nonlinear operator equations in partial ordered linear topology spaces by employing the semi-order method. Some new existence results are obtained.

partial order,mixed monotone operator,coupled solution,existence

1 Introduction

The techniques of partial order theory are used to discuss the existence of coupled solutions and coupled minimal-maximal solutions for a kind of nonlinear operator equation in a partial ordered linear topology space as follows:

where N is an increasing operator and A is a mixed monotone operator.

In 1987,Guo and Lakshmikantham[1]studied a nonlinear operator equation in a Banach space as

where A is a mixed monotone operator.They obtained some existence results of coupled solution for this operator equation.In 2005,Liu and Feng[2]considered the following operator equation:in a complete metric space and a Banach space,respectively,and by using the technique of partial order theory they obtained some existence results of solution.Very recently,He[3]has dealt with the operator equation(1.1)in Banach spaces and have given some solvability results for this kind of equations by using the concept of φ concave-ψ convex operator(see [4]).

Motivated and inspired by the above works,the main purpose of this paper is to further study the solvability of the equation(1.1).Under some suitable conditions,we give some new existence theorems for this kind of equations.To the knowledge of the author,there are very few works on the existence of coupled solutions and coupled minimal-maximal solutions for the equation(1.1)in partial ordered linear topology space,and therefore,our results generalize and improve some corresponding results.

2 Preliminaries

In this section,we give some concepts and lemmas which are necessary for proving the main results of this paper,and the other unstated concepts can be seen in[5–8].

Let E be a real linear topology space,P be a cone of E and“≤”be a partial order induced by the cone P,i.e.,for any x,y∈E,x≤y(or alternatively,denoted as y≥x)if and only if y−x∈P.We write x＜y,if x≤y and xy.

Let x,y∈E,x＜y.The set de fi ned by[x,y]={z|x≤z≤y}is called an ordered interval in E.For any subset D⊂E×E,we denote by,(D)and CD the weak closure of D,the closed convex hull of D and the complement of D,respectively.

Let

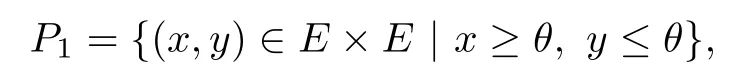
where θ denotes the zero element of E.It is easy to see that P1is a cone of the product space E×E,and P1de fi nes a partial order in E×E as follows(denoted as≺):

(x,y)≺(u,v)(or alternatively,denoted as(u,v)≻(x,y))if and only if x≤u and y≥v.

De fi nition 2.1[9−10]LetDbe a nonempty subset of a real partial order linear topology space(E,≤).

(i)The operatorA:D×D→Eis said to be mixed monotone ifA(x,y)is both nondecreasing inxand nonincreasing iny,i.e.,ifu1≤u2,v2≤v1,ui,vi∈D(i=1,2)imply

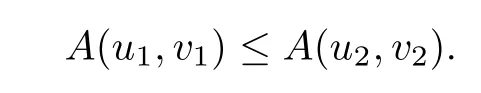
(ii)A point(x∗,y∗)∈D×D,x∗≤y∗is called a coupled solution of the nonlinear operator equation(1.1)if

(iii)A point(x∗,y∗)∈D×D,x∗≤y∗is called a coupled minimal-maximal solution of the nonlinear operator equation(1.1),if(x∗,y∗)is a coupled solution of the nonlinearoperator equation(1.1)such that for any coupled solution(u∗,v∗)of(1.1),we have

Lemma 2.1Assume thatG:D×D→ Eis a mixed monotone operator andNis a nonlinear operator.Let

Then the following conclusions hold:

(i)His an increasing operator on the partial order deduced byP1;

(ii)H(x,y)=B(x,y)has a solution(x∗,y∗)if and only if(x∗,y∗)is a coupled solution of

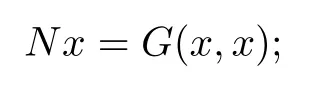
(iii)A minimal solution of

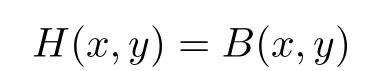
is a coupled minimal-maximal solution of

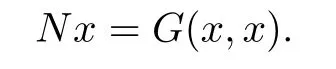
Proof.(i)For any(u1,v1),(u2,v2)∈D×D,if(u1,v1)≺(u2,v2),then it follows from the de fi nition of≺that

The mixed monotonicity of G implies that

Therefore,by the de fi nition of≺again,we have

Thus,H is an increasing operator on the partial order deduced by P1.

(ii)(x∗,y∗)is a solution of

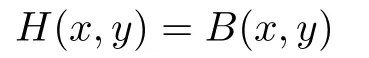
if and only if(x∗,y∗)is a solution of

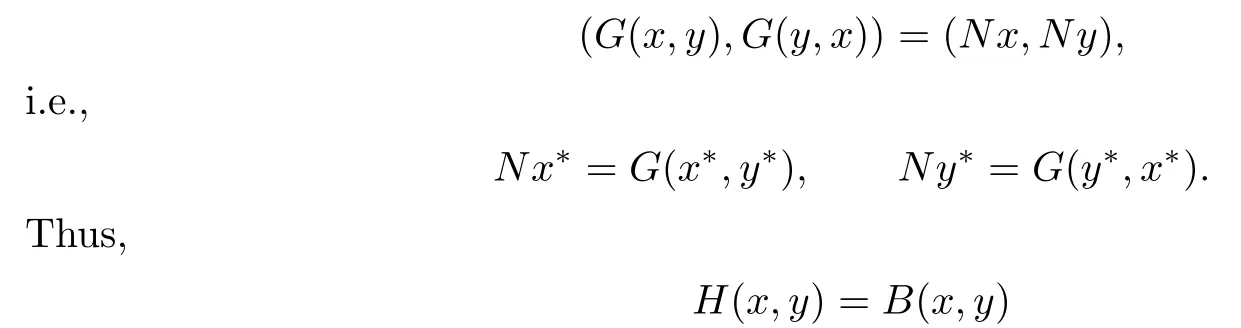
has a solution(x∗,y∗)if and only if(x∗,y∗)is a coupled solution of

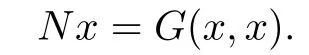
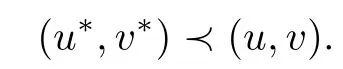
(iii)Suppose that(u∗,v∗)is a minimal solution of

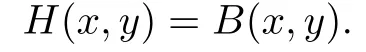
For any solution(u,v)of

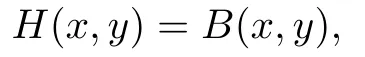
by the minimal quality,we have

Therefore,

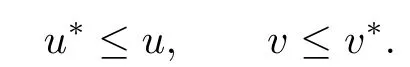
By(ii)and De fi nition 2.1,it is easy to see that(u∗,v∗)is a coupled minimal-maximal solution of

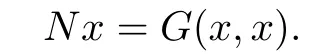
This completes the proof.

We also need the following lemmas.

Lemma 2.2[8]Assume that(E,P)is a partially ordered space,Dis a nonempty subset ofEandy∈E.Ifz≤y(ory≤z)for allz∈D,thenz≤y(correspondingy≤z)for all

Let L(E)be the space of all linear operators on E.We give the following lemma on an operator,whose proof is omitted,due to it is easy to prove.

Lemma 2.3Assume that Λ∈(0,1],T∈L(E),and(ΛI+T)−1∈L(E).Then

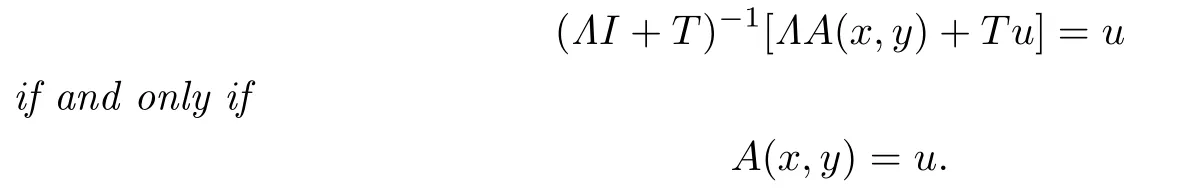
3 Main Results and Their Proofs

Our main results are the following two theorems:

Theorem 3.1LetEbe a real linear topology space,Pbe a cone ofE,u0,v0∈E,u0＜v0,D0=[u0,v0]be an ordered interval inEandNbe an increasing operator withN(D0)=D0.Assume that

is a mixed monotone operator,Λ∈(0,1],T∈L(E)and(ΛI+T)−1∈L(E)are positive operators.If the following conditions are satis fi ed:

(i)Nu0≤A(u0,v0),A(v0,u0)≤Nv0;

(ii)for anyx1,x2∈D0,Nx1≤Nx2impliesx1≤x2;

(iii)any totally ordered subset ofG(D)is relatively compact with weak topology,where

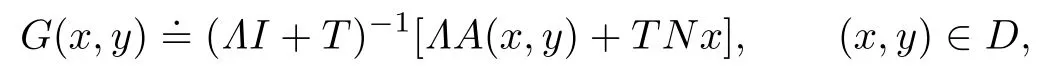
then the nonlinear operator equation(1.1)has a coupled solution(x∗,y∗)∈D.

Proof.First,we verify that the following conclusions hold:

is a mixed monotone operator and

In fact,if(x,y)∈D,then

Since N is an increasing operator with N(D0)=D0,we can get

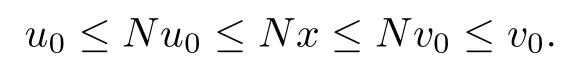
Since T∈L(E)is a positive operator,we have

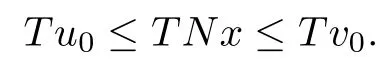
On the other hand,by the mixed monotonicity of A and the condition(i),we have

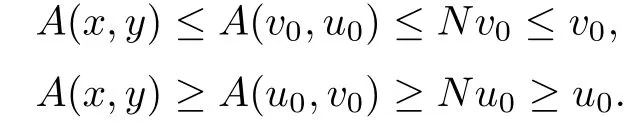
Therefore,we can get

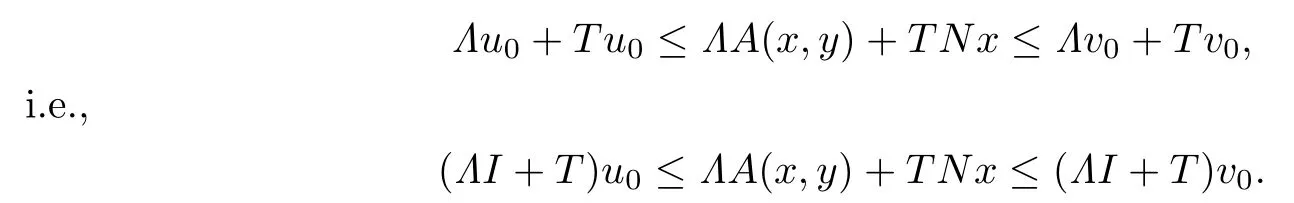
Since(ΛI+T)−1∈L(E)is a positive operator,we have

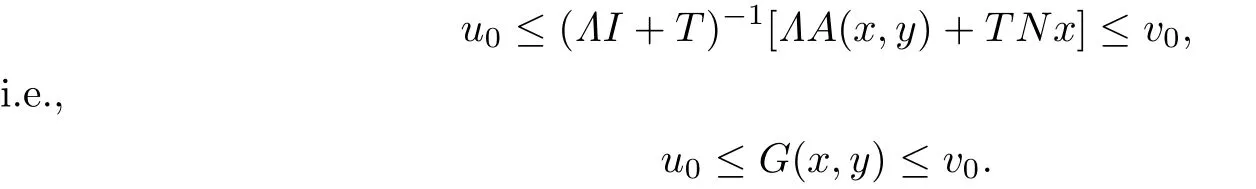
If(x1,y1),(x2,y2)∈D,and(x1,y1)(x2,y2),then

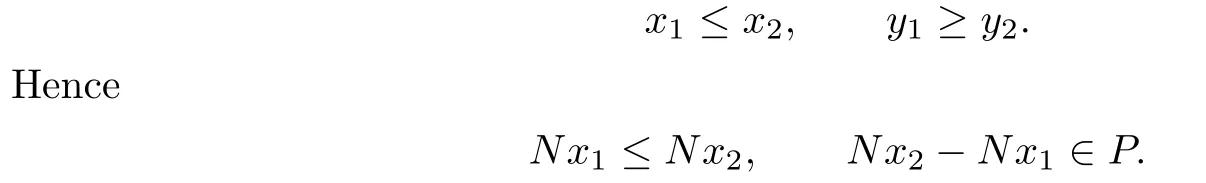
Since T∈L(E)is a positive operator,by the mixed monotonicity of A,we have T(Nx2−Nx1)∈P,i.e.,

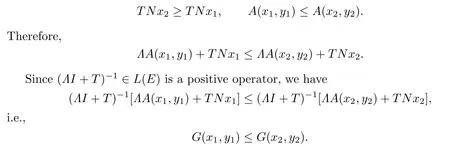
Therefore,G is a mixed monotone operator.

And then we show that

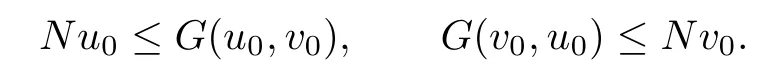
In fact,by the condition(i),we have

Hence,

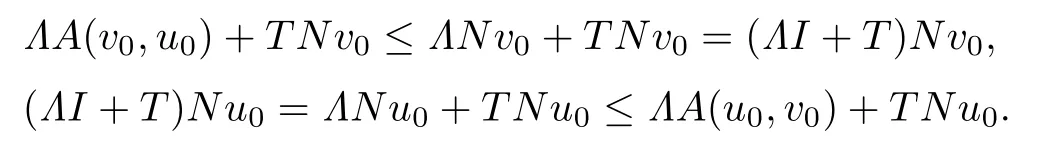
Notice that(ΛI+T)−1∈L(E)is a positive operator.Thus we have

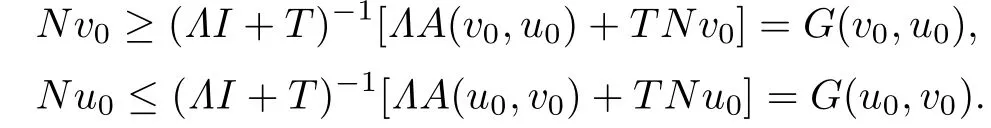
Next,we show that the nonlinear operator equation

has a solution in D,where

Step 1.By Lemma 2.1,H is an increasing operator.Let

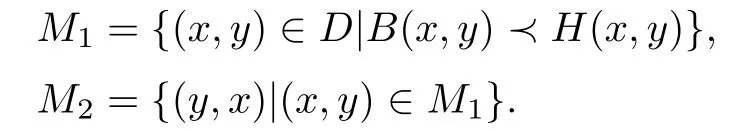
Then M16∅(since(u0,v0)∈M1).

Suppose that K1is a totally ordered subset of M1.Then K2={(y,x)|(x,y)∈K1}is a totally ordered subset of M2.For any q1∈G(K1),q2∈G(K2),let

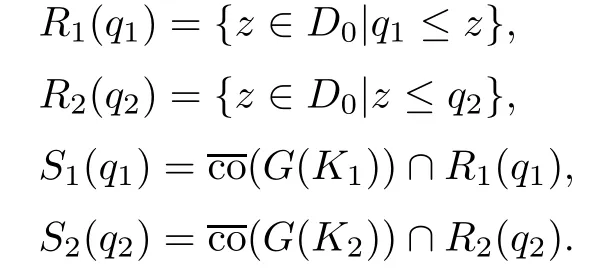
It is easy to see that R1(q1),R2(q2),S1(q1)and S2(q2)are all convex and closed sets.

Since N(D0)=D0,we know that there exist w1,w2∈D0such that

Now for any(x,y)∈K1,we have(y,x)∈K2.Hence

Therefore,

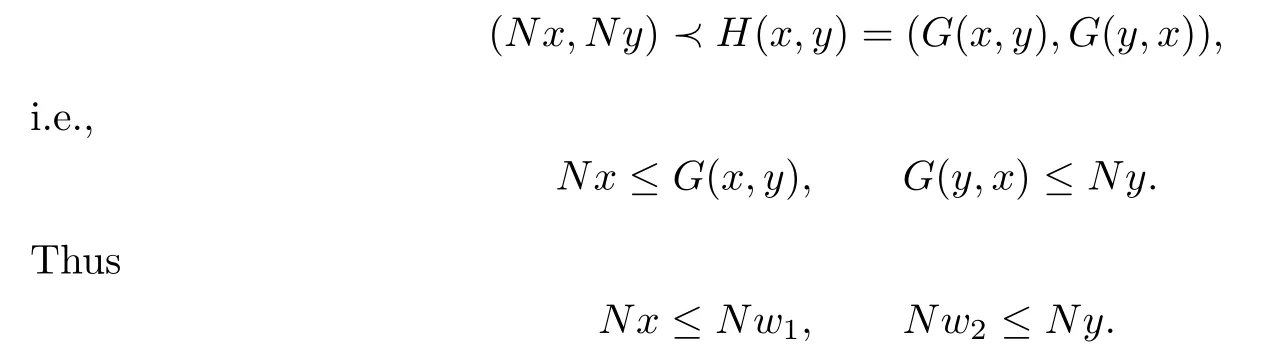
From the condition(ii),we have

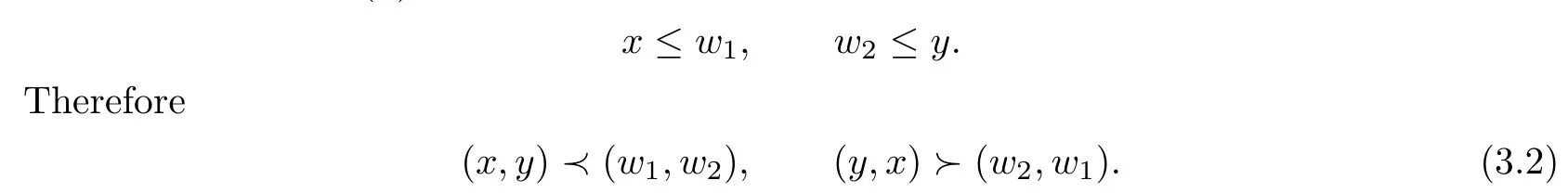
This indicates that(w1,w2)is an upper bound of K1and(w1,w2)∈M1.From Zorn’s Lemma we know that M1contains a maximal element(x∗,y∗).

Step 4. Finally we prove that the maximal element(x∗,y∗)is the solution of the nonlinear operator equation(∗).

By the de fi nition of B,the condition(ii)and N being an increasing operator,it is not difficult to check that B is also an increasing operator and if

It follows from Lemma 2.3 that

Therefore,(x∗,y∗)is a coupled solution of the equation(1.1).The proof is completed.

Theorem 3.2Assume that all conditions of Theorem3.1are satis fi ed.Then the nonlinear operator equation(1.1)has a coupled minimal-maximal solution(x∗,y∗)∈D.

Proof.Let

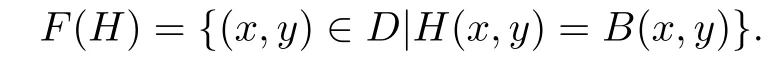
Theorem 3.1 implies that F(H)is nonempty.Let

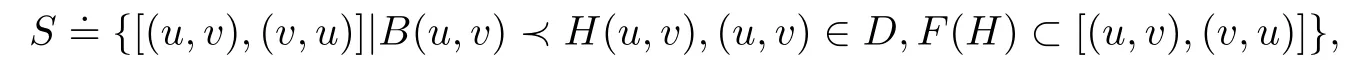
where[(u,v),(v,u)]is an ordered interval in E×E.Then S∅(since D∈S).De fi ne the relation“≤1”in S as follows:

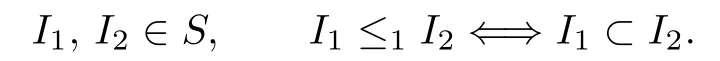
It is easy to see that“≤1”is a partial order in S.

Next we show that S has a minimal element.

Step 1. Suppose thatΓ={[(uα,vα),(vα,uα)]|α∈Λ}is any totally order subset of S, whereΛis an index set.Let

Then R1and R2are totally ordered subsets of D.It follows from the mixed monotonicity of G that G(Ri)(i=1,2)are totally ordered subsets of G(D).

Similarly to the proof of(3.5),we also get

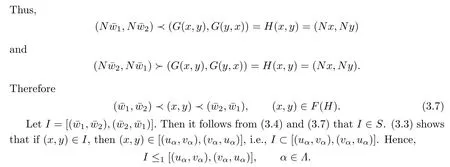
I is a lower bound ofΓin S.By Zorn’Lemma,S contains a minimal element denoted as

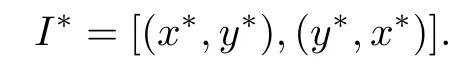
Step 3. By the de fi nition of S,we have

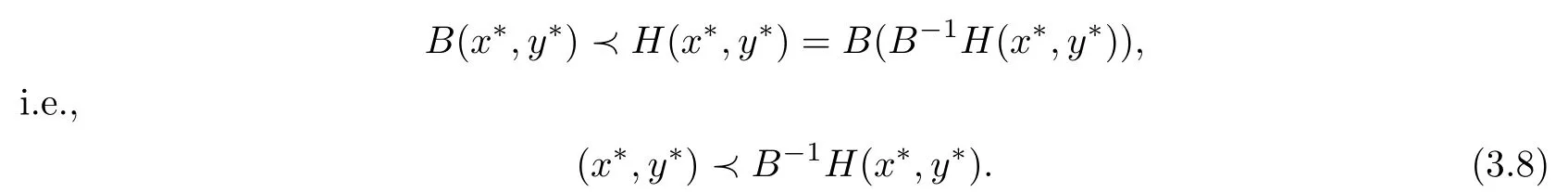
The monotonicity of H implies that

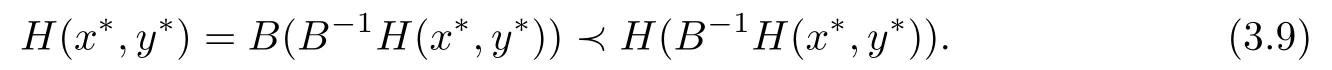
For any(x,y)∈F(H),the monotonicity of H and the de fi nition of S show that

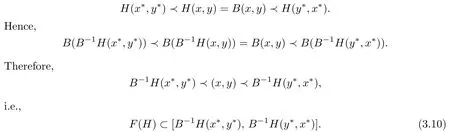
From(3.9)and(3.10)we know that[B−1H(x∗,y∗),B−1H(y∗,x∗)]∈S.

By virtue of the minimality of I∗,we get

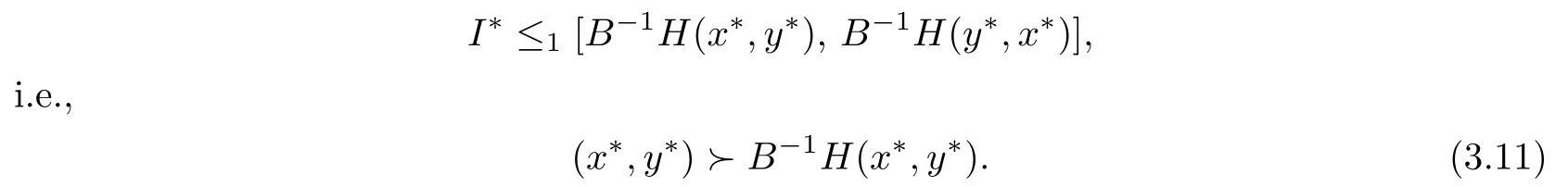
(3.8)and(3.11)indicate that

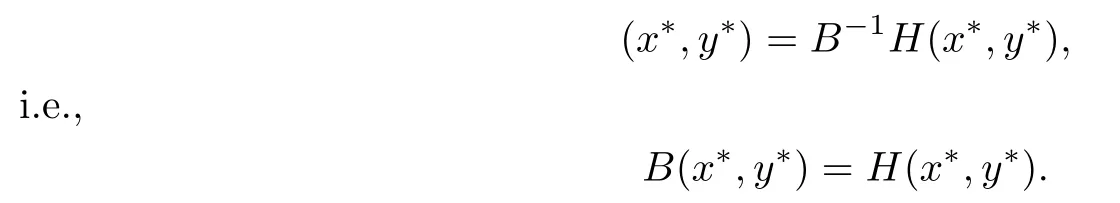
On the other hand,for any(x,y)∈F(H)⊂I∗,it is easy to see that

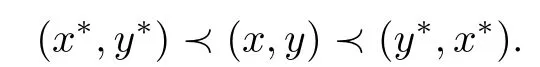
This shows that(x∗,y∗)is a minimal solution of the equation(∗).

By Lemma 2.1,(x∗,y∗)is a coupled minimal-maximal solution of

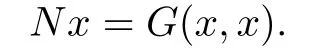
It follows from Lemma 2.3 that

Therefore,(x∗,y∗)is a coupled minimal-maximal solution of the equation(1.1).The proof is completed.

Remark 3.1In Theorems 3.1 and 3.2,we do not assume that the operators are continuous or compact,and the results hold in partial ordered linear topology space.Therefore our conclusions generalize or improve some corresponding results of[3,5,8,11–12].

[1]Guo D J,Lakshmikantham V.Couple fixed points of nonlinear operators with applications.Nonlinear Anal.,1987,11:623–632.

[2]Liu S Y,Feng Y Q.Solvability of a class of operator equations in partially ordered complete metric space and in partially ordered Banach space.Acta.Math.Sinica.,2005,48:109–114.

[3]He G,Lee B S,Huang N J.Solvability of a new class of mixed monotone operator equations with an application.Nonlinear Anal.Forum,2005,10:145–151.

[4]Xu S Y,Jia B G.Fixed-point theorems of φ concave-ψ convex mixed monotone operators and applications.J.Math.Anal.Appl.,2004,295:645–657.

[5]Duan H G,Li G Z.The existence of couple minimal-maximal quasi-solutions for a class of nonlinear operator equations.J.Math.,2005,25:527–532.

[6]Deimling K.Nolinear Functional Analsis.New York:Springer-Verlag,1985.

[7]Guo D,Lakshmikantham V.Nonlinear Problems in Abstract Cones.New York:Academic Press,1988.

[8]Liu X Y,Wu C X.Fixed point of discontinous weakly compact increasing operators and its applications to initial value problem in Banach space.J.System Sci.Math.Sci.,2000,20: 175–180.

[9]Guo D.Partial Order Methods in Nonlinear Analysis.Jinan:Shangdong Science and Technology Press,2000.

[10]Wu Y X,Liang Z D.Existence and uniqueness of fixed point for mixed monotone operators with applications.Nonlinear Anal.,2006,65:1913–1924.

[11]Syau Y R.Some fixed point theorems of T-monotone oprators.J.Math.Anal.Appl.,1997, 205:325–329.

[12]Zhang K M,Xie X J.Solution and coupled minimal-maximal quasi-solutions of nonlinear nonmonotone operator equations in Banach space.J.Math.Res.Exposition,2003,23:47–52.

Communicated by Li Yong

34C25,47H10

A

1674-5647(2012)01-0065-10

date:Jan.12,2010.

The Innovation Foundation for College Research Team of Shanxi University of Finance and Economics.