Two Generator Subsystems of Lie Triple System∗

FENG JIAN-QIANG

(Academy of Mathematical and Computer Sciences,Hebei University,Baoding,Hebei,071002)

Two Generator Subsystems of Lie Triple System∗

FENG JIAN-QIANG

(Academy of Mathematical and Computer Sciences,Hebei University,Baoding,Hebei,071002)

For a Lie triple systemTover a field of characteristic zero,some sufficient conditions forTto be two-generated are proved.We also discuss to what extent the two-generated subsystems determine the structure of the systemT.One of the main results is thatTis solvable if and only if every two elements generates a solvable subsystem.In fact,we give an explicit two-generated law for the two-generated subsystems.

Lie triple system,two generated subsystem,solvable

1 Introduction

Lie triple system(L.t.s.)is a generalization of the concept of Lie algebra,since every Lie algebra L is also an L.t.s.with the multiplication

And also every L.t.s.is a subsystem of an L.t.s.coming from a Lie algebra,due to the concept of standard imbedding.Hence L.t.s.is strongly linked to Lie algebra,and many results of Lie algebra can be generalized in an appropriate form,to the L.t.s.(see[1–5]). In this section we recall some de fi nitions and facts about L.t.s.We start with the de fi nition of an L.t.s.(see[1–2]).

De fi nition 1.1A Lie triple system(L.t.s.)is a vector spaceTover a fieldK,which is closed with respect to a trilinear multiplication[·,·,·]and satis fies

whereu,v,x,y,z∈T.

A derivation of an L.t.s.T is a linear transformation D of T such that

For x,y,z∈T,de fi ne linear transformations L(·,·),R(·,·)on the vector space T by

We can see by the de fi nition of T that all L(x,y),x,y∈T,are derivations.A derivation D of the form

is called an inner derivation.

A subspace U of T is called an ideal of T if for all x,y∈T,u∈U we have[uxy]∈U. For any submodule V in T,the centralizer ZT(V)of V in T is de fi ned by

In particular,ZT(T)is called the center of T and denoted simply by Z(T).An L.t.s.T is called abelian if it satis fies

For an ideal V of an L.t.s.T,de fi ne the lower central series(see[6])for V by

Then V is called T-nilpotent if Vm=0 for some m.It is called nilpotent if it is T-nilpotent. Put

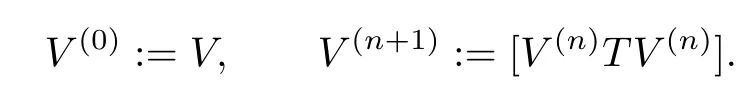
Then V is called solvable if there is a positive integer k for which V(k)=0.T is solvable if it is a solvable ideal.

The Frattini subsystem F(T)of an L.t.s.T is the intersection of all maximal subsystems of T.The Frattini ideal φ(T)is the largest ideal of T contained in F(T).

For a subset U of an L.t.s.T,hUi denotes the subsystem of T generated by U.

2 Two Generated Subsystems of L.t.s.

In this section we give some results about two generated subsystems of L.t.s.,which are generalisations of corresponding results of Lie algebras(see[7]).

De fi nition 2.1LetTbe an L.t.s.For arbitraryx,y∈T,the subsystemhx,yigenerated byx,yis called a two-generated subsystem.Tis called two-generated if it is a two-generated subsystem of itself.

Lemma 2.1An L.t.s.Tis two-generated if and only ifT/φ(T)is two-generated.

Proof.Let π be the natural homomorphism from T to T/φ(T),that is,

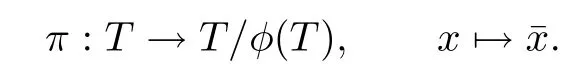
Evidently,T=hx,yi implies that

Now suppose that

which is a contradiction and the proof is completed.

De fi nition 2.2Suppose thatVis a subspace of an L.t.s.T.The normalizerNT(V)ofVinTis de fi ned by

Lemma 2.2(1)IfVis a subspace ofT,thenN(T,V)is a subsystem ofT;

(2)IfVis a subsystem ofT,thenNT(V)=V+N(T,V);

(3)IfVis a subsystem ofT,thenVis an ideal ofNT(V);

(4)IfVis an ideal ofT,thenNT(V)is an ideal ofT.

Proof.(1)Notice that by de fi nition[xyz]∈V if two of x,y,z belong to V and N(T,V) respectively.Now for all x,y,z∈N(T,V),v∈V,t∈T,by the identity(3)we have

Similarly,[[xyz]tv]∈V.

(2)Clearly,we only need to prove that V+N(T,V)is a subsystem.If all x,y,z belong to V or N(T,V),then by assumption and(1),[xyz]∈V+N(T,V).Otherwise,by the de fi nition of N(T,V),we also have[xyz]∈V+N(T,V).

(3)Clearly,V⊆NT(V).Then(3)follows from the de fi nition of N(T,V)and(2).

(4)We only need to prove that N(T,V)is an ideal of T.By using the identity(3),the proof is similar to that of(1).

Lemma 2.3IfSis a subsystem of a nilpotent L.t.s.TandST,thenNT(S)S. Proof.Since T is nilpotent,there is a p such that

that is,x∈N(T,S)⊆NT(S).So NT(S)S.The proof is completed.Theorem 2.1LetTbe a simple L.t.s.over a fieldK.Assume that every proper subsystem ofTis nilpotent.Then the following hold:

(1)M1∩M2=0for every pair of different maximal subsystemM1andM2ofT;

(2)there is nox(60)∈Tsuch thatR(x,x)is a nilpotent linear transformation onT;

(3)Tis two-generated.

Proof.(1) Let M be a maximal subsystem of T.Assume that there exists a proper subsystem S of T such that dimM∩S is maximal.By Lemma 2.3,the nilpotency of M and S implies that

Let U be the subsystem of T generated by NM(M∩S)and NS(M∩S).Since M∩S is a non-zero ideal of U,it follows from the simplicity of T that UT.Moreover,S∩M is properly contained in U∩M,which contradicts our choice of S.

and proved the following:

Theorem 2.2LetLbe a finite dimensional Lie algebra over an in finite fieldKof characteristicp＞5.ThenLis solvable if and only if for somenthe identityen≡0holds inL.

We can generalize this to L.t.s.

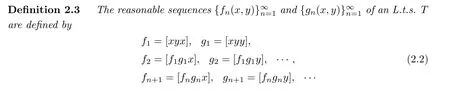
Theorem 2.3LetTbe a finite dimensional L.t.s.over a field of characteristic zero. ThenTis solvable if and only if for somenthe identityfn≡0(orgn≡0)holds inT.SoTis solvable if and only if every two elements generate a solvable subsystem.

Proof.We only need to prove the first assertion.If T is solvable,then it satis fies an identity of the form fn≡0(or gn≡0)since for any x,y∈T the value fn≡0(or gn≡0)belongs to the corresponding term of the derived series T(n).To prove sufficiency,we use the standard imbedding.If T is not solvable,then L(T)=T⊕L(T,T)is not solvable.So Theorem 2.2 tells us that for any n∈N,en(x,y)≡0 can not hold.Notice that by de fi nition fn(x,y) (resp.gn(x,y))in T is just(x,y)(resp.)in L(T),so,both fn≡0 and gn≡0 cannot hold.The theorem is proved.

Corollary 2.1LetTbe an L.t.s.over a field of characteristic zero andL(T)be its standard imbedding.Then every two elements ofTgenerates a solvable subsystem ofTif and only if every two elements ofL(T)generates a solvable subalgebra ofL(T).

Recall that the Engel sequence{vi}on a Lie algebra L is de fi ned by

Similarly we give the following:

De fi nition 2.4LetTbe a Lie triple system.The Engel sequence{wi}onTis given by

For the Engel sequence{wi}of a Lie triple system T,we have the following theorem.

Theorem 2.4LetTbe a Lie triple system,and{wi}the Engel sequence ofT.Ifwk≡wl

holds inTforkl,thenTis solvable.

Proof.Let L(T)=T∔L(T,T)be the standard imbedding of T and{vi}the Engel sequence of L(T).Then it is easy to see that for all x,y∈T we have

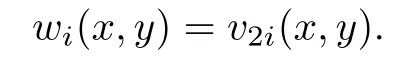
Hence that wk≡wlholds in T implies that v2k≡v2lholds in L(T),which means that L(T) is solvable(see Proposition 3.3 of[7]).Therefore T is solvable.The proof is completed.

We conclude this paper by the following collection of some classes of L.t.s.which behave like solvable Lie triple systems.For short,we will say that the property P satis fies the condition

(∗)if for every L.t.s.T all of its two-generated proper subsystems possess the property P,then either T itself possesses the property P or T is two-generated.

Then we have

Theorem 2.5(1)The class of abelian L.t.s.satis fies the condition(∗);

(2)The class of nilpotent L.t.s.satis fies the condition(∗);

(3)The class of solvable L.t.s.satis fies the condition(∗).

Proof.(1)is clear.

(2)By assumption,for all x,y∈T,hx,yi is nilpotent.Thus

for some n(cf.[6]).Hence

where d is the dimension of the standard imbedding L(T)of T.Since the above assertion holds for any y∈T,R(x,x)is nilpotent for all x∈T.It follows from Engel’s theorem for Lie triple systems that T is nilpotent.

(3)It follows from Theorem 2.4.

[1]Lister W G.Structure theory of Lie triple systems.Amer.Math.Soc.,1952,72:217–242.

[2]Meyberg K.Lecture on Algebra and Triple Systems.Charlottesville,USA:Univ.of Virginia, 1972.

[3]Zhang Z,Shi Y,Zhao L.Invariant symmetric bilinear forms on Lie triple system.Comm.Algebra, 2002,30:5563–5573.

[4]Zhang Z,Chen L,Liu W,Bai X.The Frattini subsystem of Lie triple system.Comm.Algebra, 2009,37:3750–3759.

[5]Feng J.Metrisable Lie triple systems.Acta.Math.Sinica(Chinese Series),2008,51:457–468.

[6]Hopkins N C.Nilpotent ideals in Lie and anti-Lie triple triple systems.J.Algebra,1995,178: 480–492.

[7]Grunewald F,Kunyavskii B,Nikolova D,Plotkin E.Two-variable identities in proups and Lie algebras.Zap.Nauchn.Sem.(POMI),2000,272:161–176.

Communicated by Du Xian-kun

17A40,17B05

A

1674-5647(2012)01-0091-06

date:July 14,2010.

The NSF(A2007000138)of Hebei Provience.