Quasi-periodic Solutions of the General Nonlinear Beam Equations∗

GAO YI-XIAN

(1.College of Mathematics and Statistics,Northeast Normal University,

Changchun,130024)

(2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun,130012)

Quasi-periodic Solutions of the General Nonlinear Beam Equations∗

GAO YI-XIAN1,2

(1.College of Mathematics and Statistics,Northeast Normal University,

Changchun,130024)

(2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun,130012)

In this paper,one-dimensional(1D)nonlinear beam equations of the form

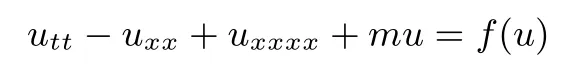
with Dirichlet boundary conditions are considered,where the nonlinearity f is an analytic,odd function and f(u)=O(u3).It is proved that for all m∈(0,M∗]⊂R (M∗is a fixed large number),but a set of small Lebesgue measure,the above equations admit small-amplitude quasi-periodic solutions corresponding to finite dimensional invariant tori for an associated in finite dimensional dynamical system.The proof is based on an in finite dimensional KAM theory and a partial Birkho ffnormal form technique.

beam equation,KAM theorem,quasi-periodic solution,partial Birkho ff normal form

1 Introduction and Main Result

Consider the general nonlinear beam equations of the form

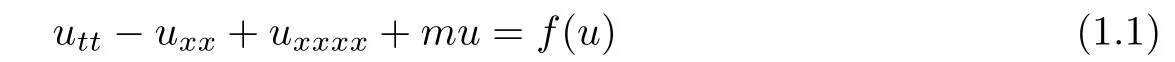
on the finite x-interval[0,π]with Dirichlet boundary conditions

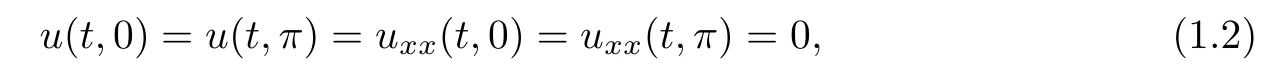
where the parameter m∈(0,M∗]⊂R,the nonlinearity f is assumed to be real analytic in u and of the form

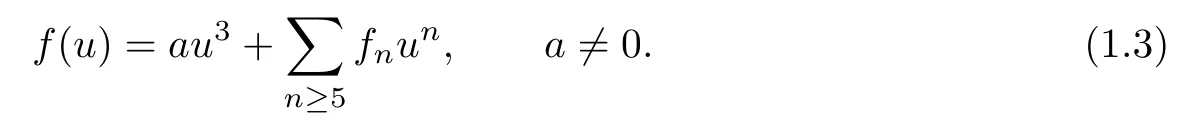
We study the equations of the form(1.1)as a Hamiltonian system on

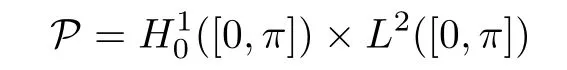
with coordinates u and v=ut.Then the Hamiltonian is

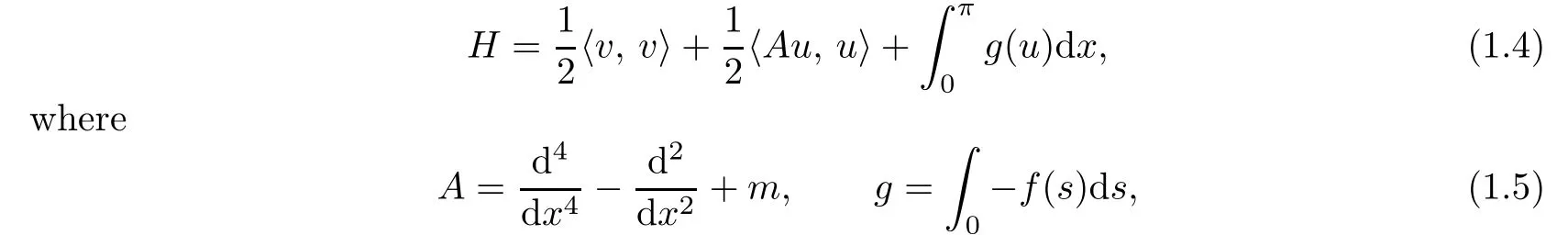
and h〈·,·〉denotes the usual scalar product in L2.Then(1.1)can be written in the form

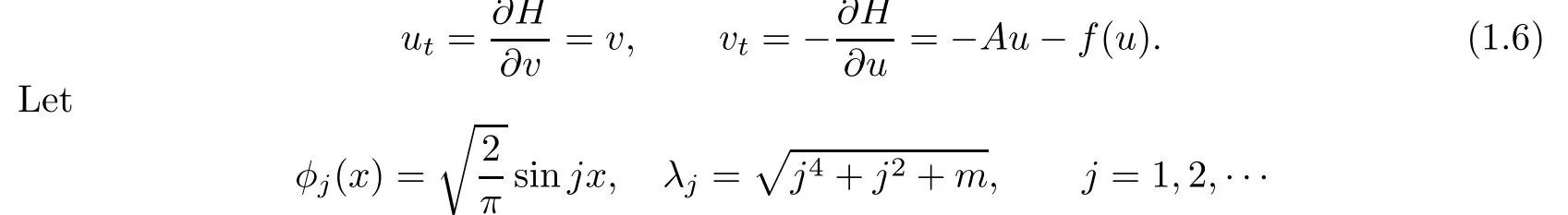
be the basic modes and frequencies of the linear equation

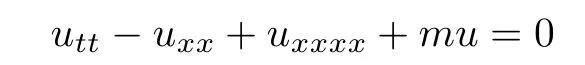
with Dirichlet boundary conditions(1.2).Then every solution of the linear equation is the superposition of their harmonic oscillations and of the form

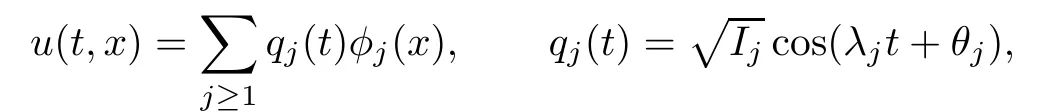
with amplitudes Ij≥0 and initial phases θj.The motions are periodic or quasi-periodic, respectively,depending on whether one or finitely many eigenfunctions are excited.In particular,for every choice

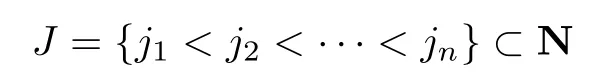
of finitely many modes there exists an invariant 2n-dimensional linear subspace EJwhich is completely foliated into rotational tori with frequencies λj1,···,λjn:

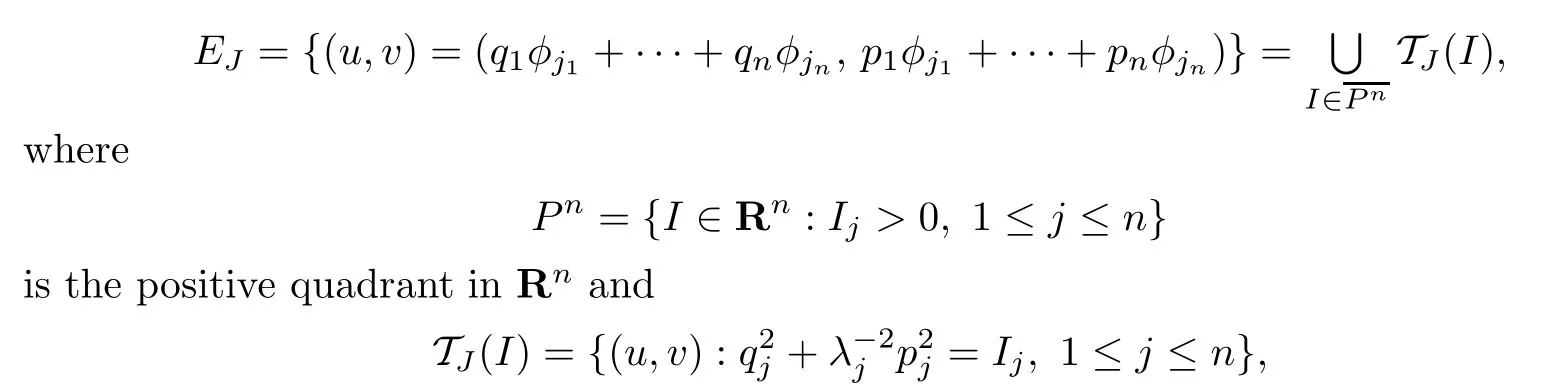
by using the above representations of u and v.In addition,such a torus is linearly stable, and all solutions have zero Lyapunov exponents.

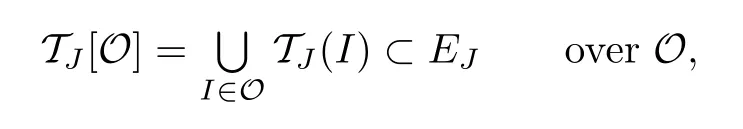
Upon restoration of the nonlinearity f,we show that there exist a Cantor set O⊂Pn, a family of n-tori and a Whitney smooth embeddingΦ:TJ[O]→EJ⊂P,such that the restriction ofΦto each TJ(I)in the family is an embedding of a rotational n-torus for the nonlinear equations. The image E of TJ[O]is called the Cantor manifold of rotational d-tori in[1].

Theorem 1.1(Main Theorem)Suppose that the nonlinearityfis real analytic and of the form(1.3).Then for each index setJ={j1＜···＜jn},there exists,for allm∈(0,M∗]⊂R,but a set of small Lebesgue measure,a Cantor manifoldEJgiven by a Whitney smooth embedding Φ:TJ[O]→ EJ,which is a higher order perturbation of the inclusion map Φ0:EJ→ Prestricted toTJ[O].Moreover,the Cantor manifoldEJis foliated by real analytic,linearly stable,n-dimensional invariant tori carrying quasi-periodic solutions.

Their starting point is to take(1.1)as a perturbed sine-Gordon equation.This result is regained by Pschel[1]by the in finite KAM theory and the normal form technique.Later, the existence of quasi-periodic solutions of the Hamiltonian partial differential equations have been studied in[2–8].In this paper,by using the KAM approach originating from [9–11],we can obtain that(1.1)admits small-amplitude quasi-periodic solutions for all m∈(0,M∗]⊂R(M∗is a fixed large number),but a set of small Lebesgue measure.

2 An In finite-dimensional KAM Theory

We consider a small perturbation of in finitely dimensional Hamiltonian in the parameter dependent form

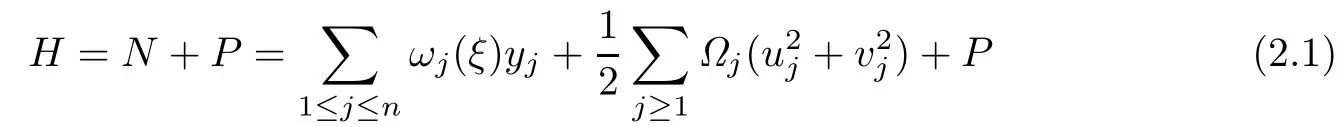
in n dimensional angle-action coordinates(x,y)and in finite-dimensional Cartesian coordinate(u,v)with symplectic structure

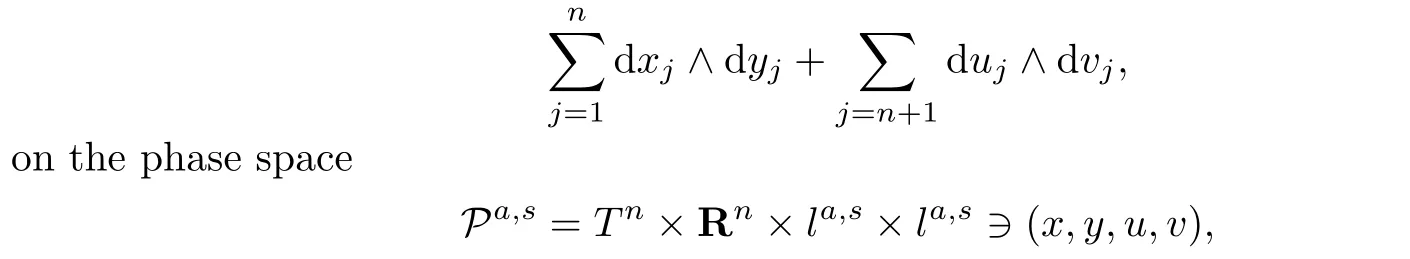
where Tnis the usual n torus with 1≤n＜∞.The tangent frequencies ω=(ω1,···,ωn) and the normal frequenciesΩ=(Ω1,Ω2,···)depend on n parameters ξ∈O⊂Rn.O is a closed bounded set of positive Lebesgue measure.

As in[2],we set

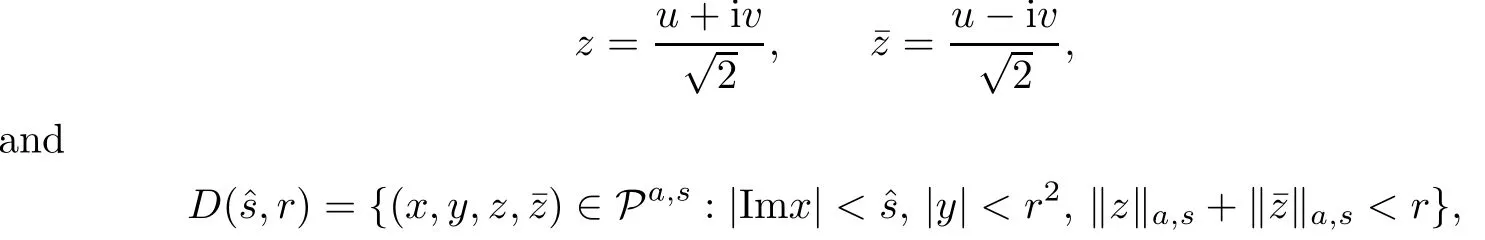
where|·|denotes the sup-norm for the complex vector anda,sis the norm in the space la,s,which are to be de fi ned later.We de fi ne the weighted phase norm

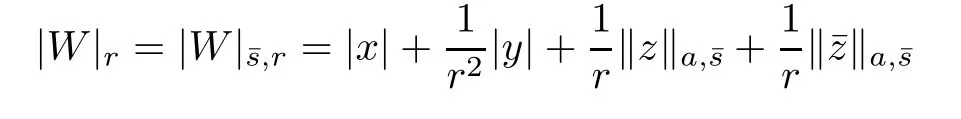
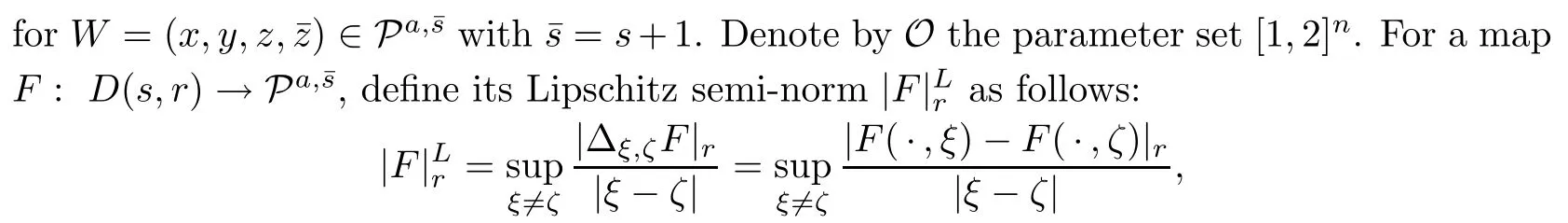
where the supremum is taken over O.

For each ξ∈O,there is an n-torus

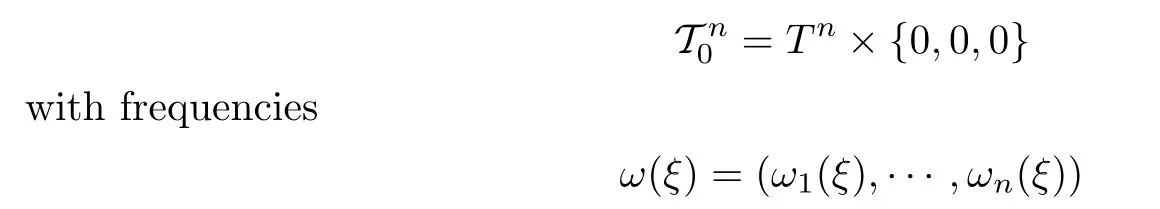
of the linear integrable Hamiltonian N.In its norm space,described by u-v coordinates,the origin is an elliptic fixed point with characteristic frequenciesΩ(ξ).The KAM theorem by Pschel[11]shows the existence of this linear stable rotational tori under a small perturbation P.In order to obtain the result we have to give some assumptions:

(A1)Non-degeneracy.The real map ξ→ ω(ξ)is Lipeomorphism between O and its image.Moreover,for all integer vectors(k,l)∈Zn×Z∞with 1≤|l|≤2,

(A3)Regularity.The perturbation P(x,y,u,v)is real analytic for a real argument (x,y,u,v)∈D(r,s)for any given r,s＞0,and Lipschitz in the parameter ξ∈O.For each ξ∈O,its gradients with respect to u,v satisfy

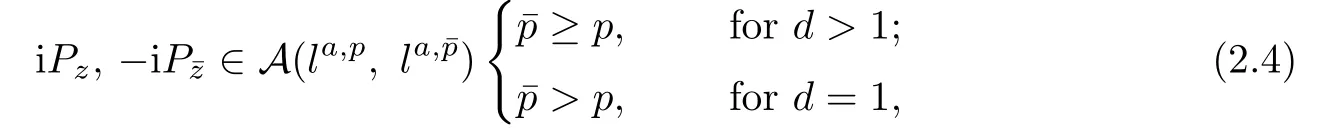
where A(la,p,)denotes the class of the maps from some neighborhoods of the origin ininto,which is real analytic in the real and imaginary parts of the complex coordinates. To state Pschel’s theorem we assume that

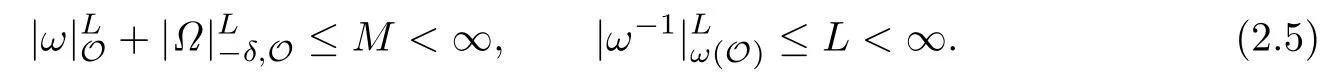
Moreover,we introduce the notations

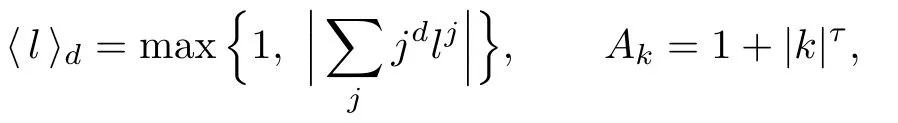
where τ＞n+1 will be fixed later.Finally,let

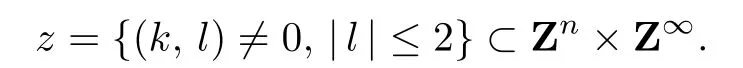
We now state the basic KAM Theorem which is recited from[11].

Theorem 2.1Suppose thatH=N+Psatis fies(A1)–(A3),and

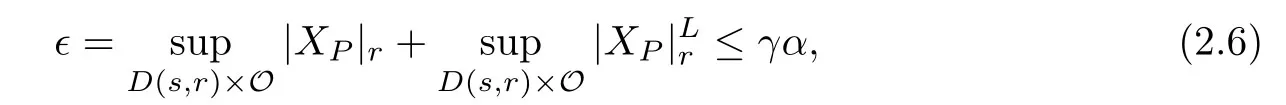
where0＜α≤1is another parameter,andγdepends onn,τands.Then there exist a Cantor setOα⊂Owith

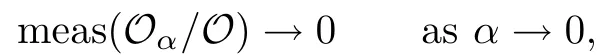
a Lipschitz continuous family of torus embedding Φ:Tn×Oα→ Pa,¯p,and a Lipschitz continuous map:Oα→Rn,such that for eachξ∈Oα,the map Φ restrictedTn×{ξ}is a real analytic embedding of rotational torus with frequencies(ξ)for the HamiltonianHatξ.

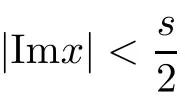
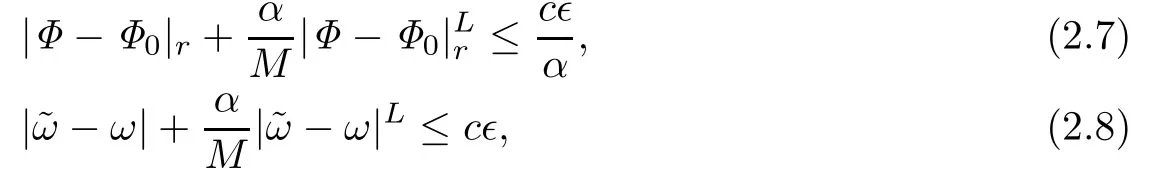
uniformly on that domain andOα,where Φ0:Tn×O→is the trivial embedding,andc≤γ−1depends on the same parameters asγ.

Moreover,there exist Lipschitz mapsωνand ΩνonOforν≥1satisfying

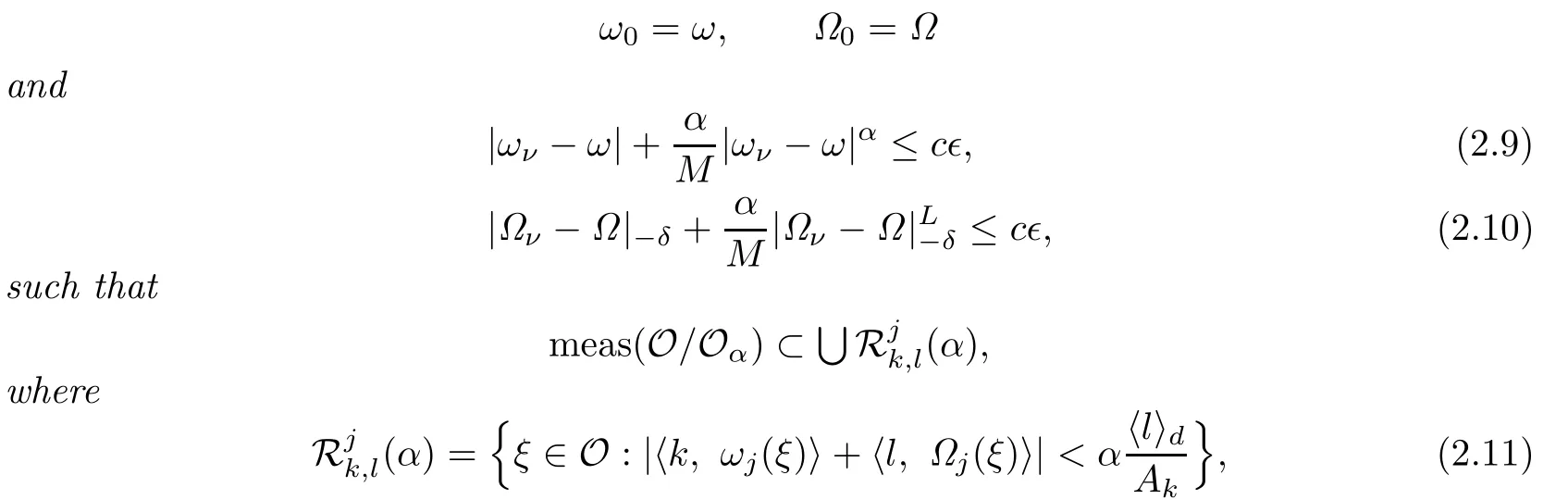
and the union is taken over allj≥0and(k,l)∈Zn×Z∞such that|k|＞K02j−1forj≥1with a constantK0≥1depending onnandτ.

Concerning the measure of the bad frequency set O/Oα,we have the following theorem.

Theorem 2.2([11],Theorem D)Suppose that in Theorem2.1the unperturbed frequencies are affine functions of the parameters.Then there is a constant˜csuch that

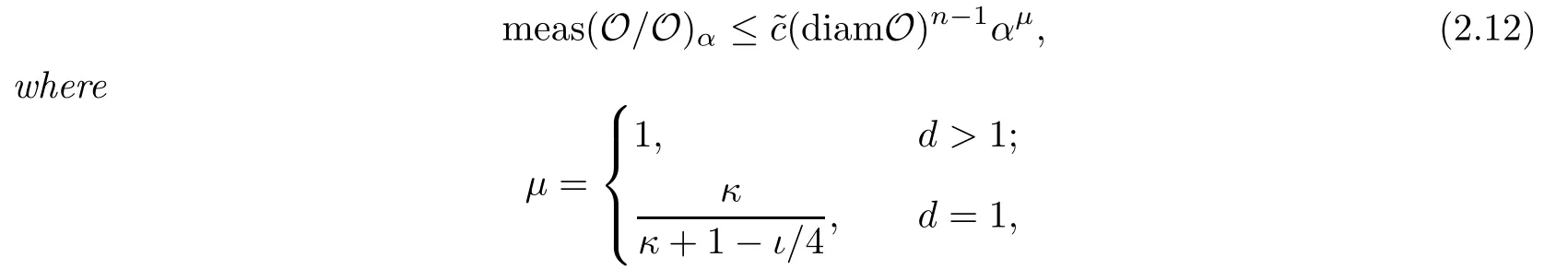
for all sufficiently smallα,andιis any number with0≤ι＜min{−p,1}.In the cased=1,κis a positive constant such that

uniformly onO.

3 The Hamiltonian for the General Beam Equations

We recall that the Hamiltonian of our nonlinear beam equation is

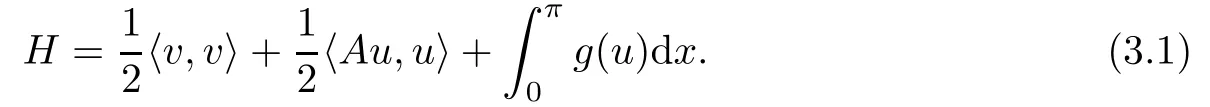
As in[1],we introduce coordinates q=(q1,q2,···),p=(p1,p2,···)through the relations

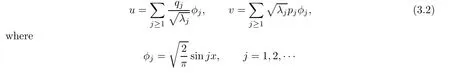
are the normalized Dirichlet eigenfunctions of the operator A with eigenvalues

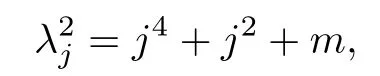
and the coordinates q and p are taken from the Hilbert space la,s.We obtain the Hamiltonian

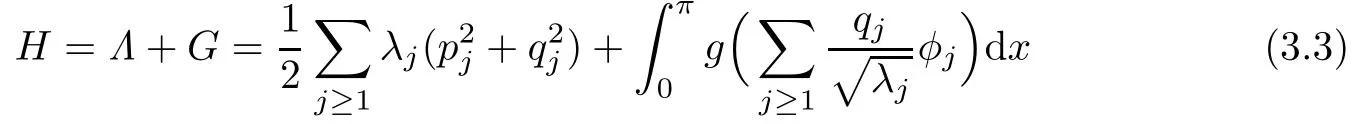
with the lattice Hamiltonian equations

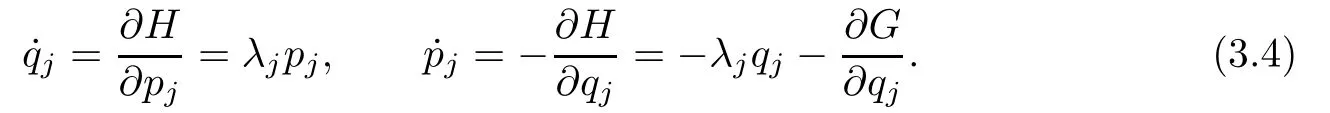
Instead of discussing its validity,we just take the latter Hamiltonian as our new starting point and make the following simple observation.

Lemma 3.1Leta≥0,s＞0,Ibe an interval,andt∈I→(q(t),p(t))be a real analytic solution of(3.4)such that

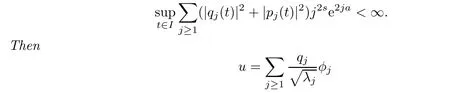
is an analytic solution of(1.1).

Next we consider the regularity of the vector field of G.Let l2be the Hilbert space of bi-in finite square summable sequences with complex coefficients.For a≥0 and s＞0,let the subspace la,s⊂l2consist of,by de fi nition,all bi-in finite sequences with the finite norm

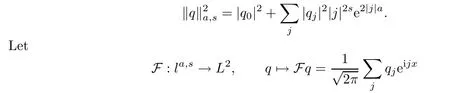
be the inverse discrete Fourier transform,which de fi nes an isometry between the two spaces, where L2is all square-integrable complex valued functions on[−π,π].Through F we can de fi ne subspaces Wa,s⊂L2that are normed by setting

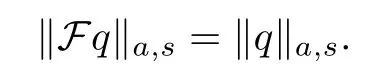
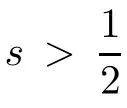
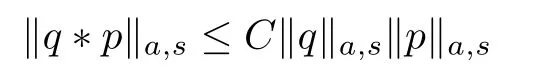
with a constantCdepending on s.Consequently,Wa,sis a Hilbert algebra with respect to multiplication of functions.

Lemma 3.3Fora≥0ands＞0,the vector fieldXGis a map from some neighborhoods of the origin inla,sintola,s+2,with

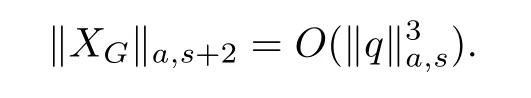
Proof.In a sufficient small neighborhood of the origin,we can consider the nonlinearity f=u3.Due to

where the constant c may be different at each appearance.Hence

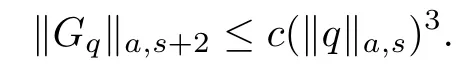
The regularity of XGfollows from the regularity of its components.

For the nonlinearity u3we find

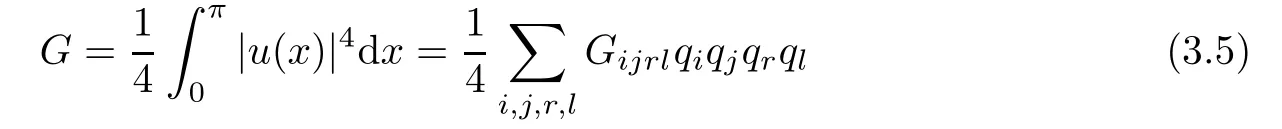
with

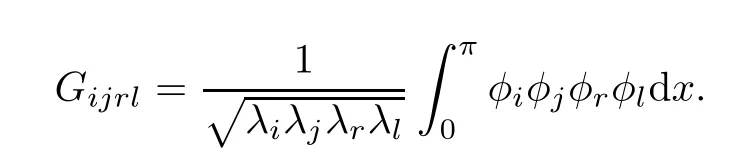
It is not difficult to verify that Gijrl=0 unless±i±j±r±l=0 for some combination of plus and minus signs.Particularly,we have

by the elementary calculation.In the following,we focus on the nonlinearity u3,since a non-zero coefficient in front of u3and all terms of order fi ve or more make no di ff erence.

Next we transform the Hamiltonian(3.3)into some partial Birkho ffform of order four so that it may serve as a small perturbation of some nonlinear integrable system in a sufficiently small neighborhood of the origin.we introduce the complex coordinates

Then the Hamiltonian is given by

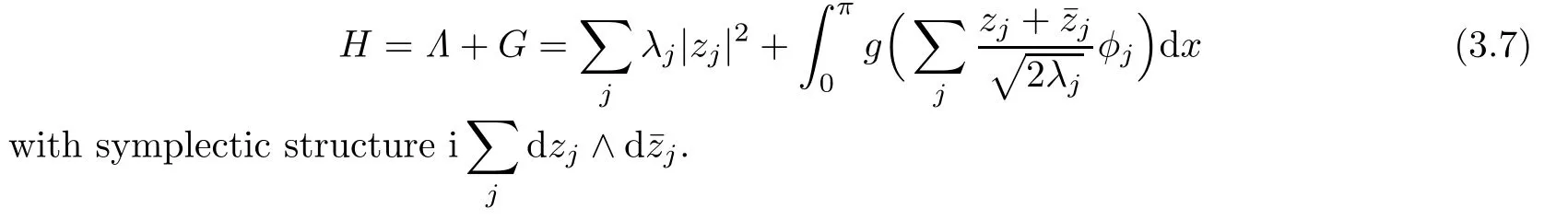
Lemma 3.4If{i,j,r,l}are nonzero integers such thati±j±r±l=0,but(i,j,r,l)(p,−p,q,−q),then for allm∈(0,M∗]⊂R,but a set of small Lebesgue measure,we have|λi±λj±λr±λl|≥c,wherecis a constant depending onm.

Proof.Without loss of generality,we may assume that i≤j≤r≤l.The condition i±j±r±l=0 then reduces to two possibilities,either i−j−r+l=0 or i+j+k−l=0. We have to study divisors of the form

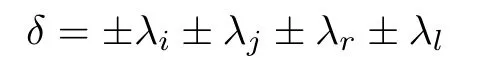
for all possible combinations of plus and minus signs.To this end,we distinguish them according to their number of minus signs.To shorten notation we let,for example,

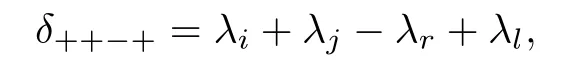
and similarly,for all other combinations of plus and minus signs.

Case 0.No minus sign.This is trivial.

Case 1.One minus sign.Obviously,

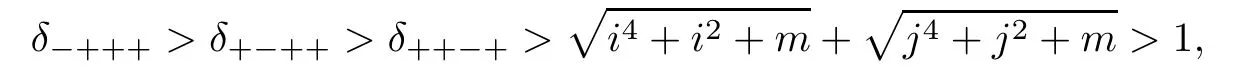
so it suffices to study δ=δ+++−.We consider δ as a function of m and notice that

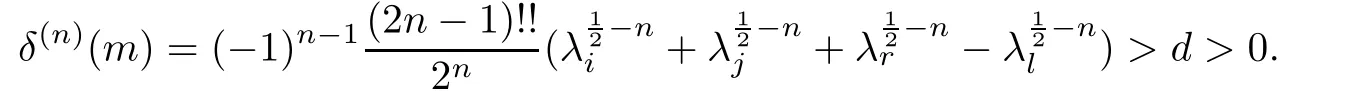
According to Lemma 5.1 in the Appendix,

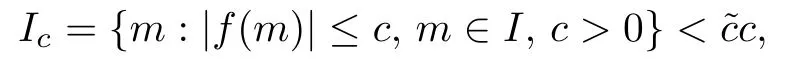
so after excising a set of small measure,we obtain that δ(m)＞c.

Case 2.Two minus signs.Here we have δ−+−+,δ−−++＞δ+−−+,and all other cases reduce to these ones by inverting the signs.So it suffices to study δ(m)=δ+−−+.Let

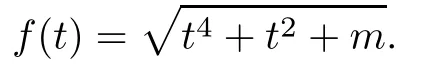
It is easy to verify that for t≥1,

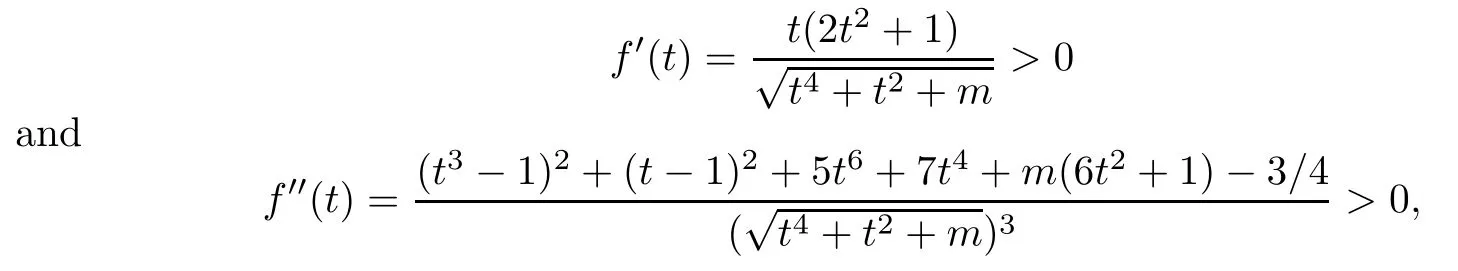
so f is increasing and convex for t≥1.Hence we have

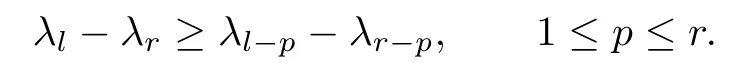
In the case l=i+j+r,we thus obtain

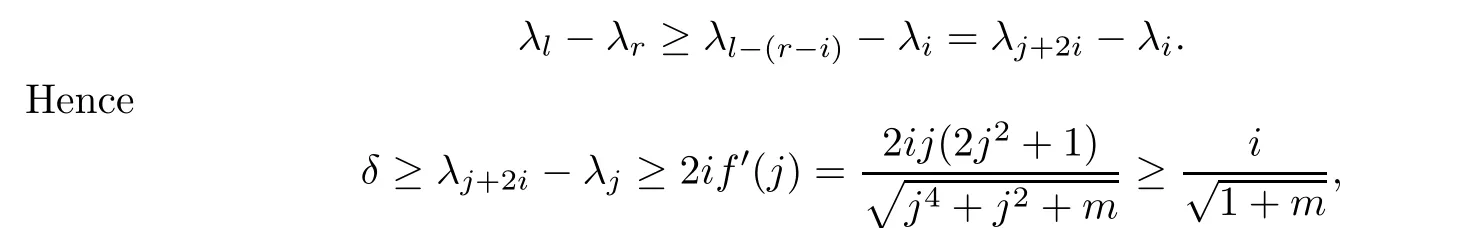
by using the mean value theorem and the monotonicity of f′.With the other alternative, we have

Cases 3 and 4.Three and four minus signs.These ones can be reduced to Cases 1 and 0,respectively.

Proposition 3.1For any index setJ={j1＜···＜jn},and allm∈(0,M∗]⊂R,but a set of small Lebesgue measure,there exists a change of coordinates Γ in a neighborhood of the origin inla,ssuch that the Hamiltonian

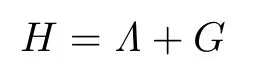
with the nonlinearity(3.5)is changed into

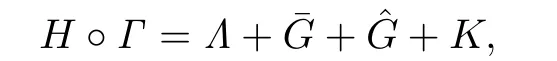
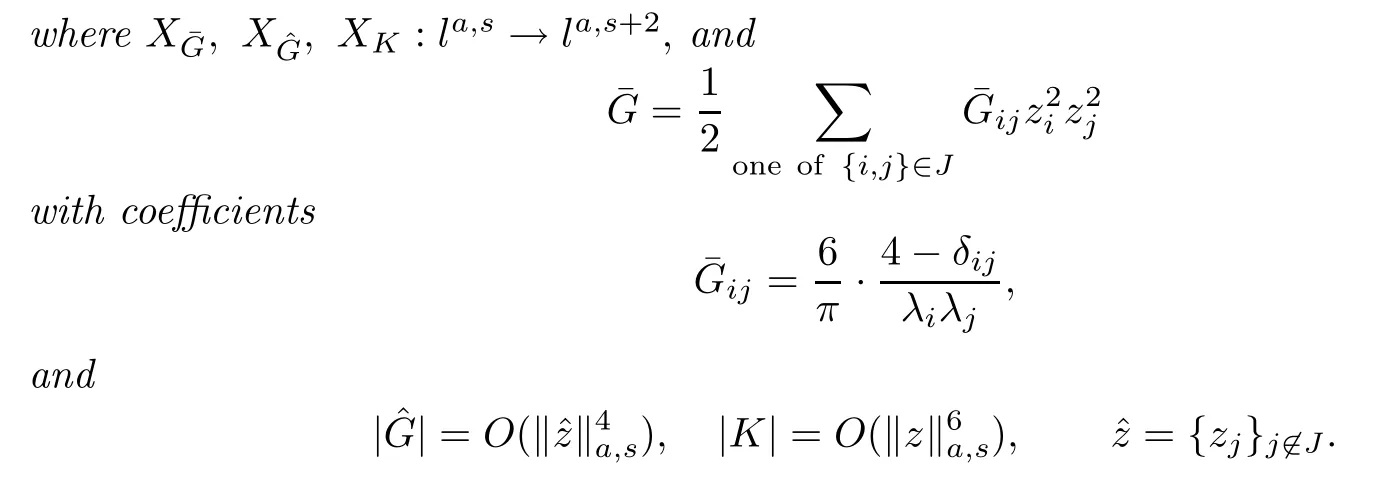
Moreover,the dependence of Γ onmis real analytic for almost all compactm-interval in(0,+∞).

Proof.It is convenient to introduce coordinates(···,w−2,w−1,w1,w2,···)in la,sby setting

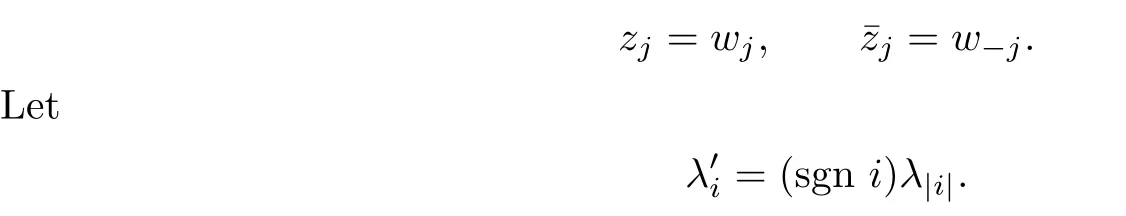
The Hamiltonian under consideration then reads as

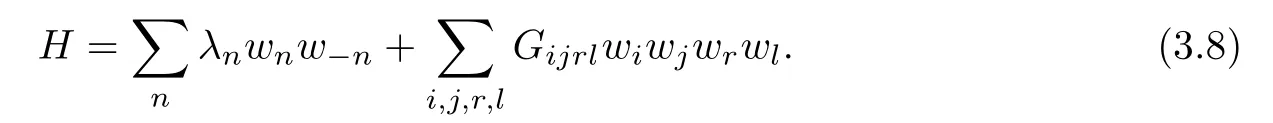
Consider a Hamiltonian function

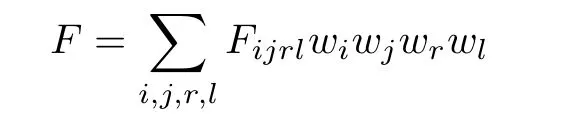
with coefficients

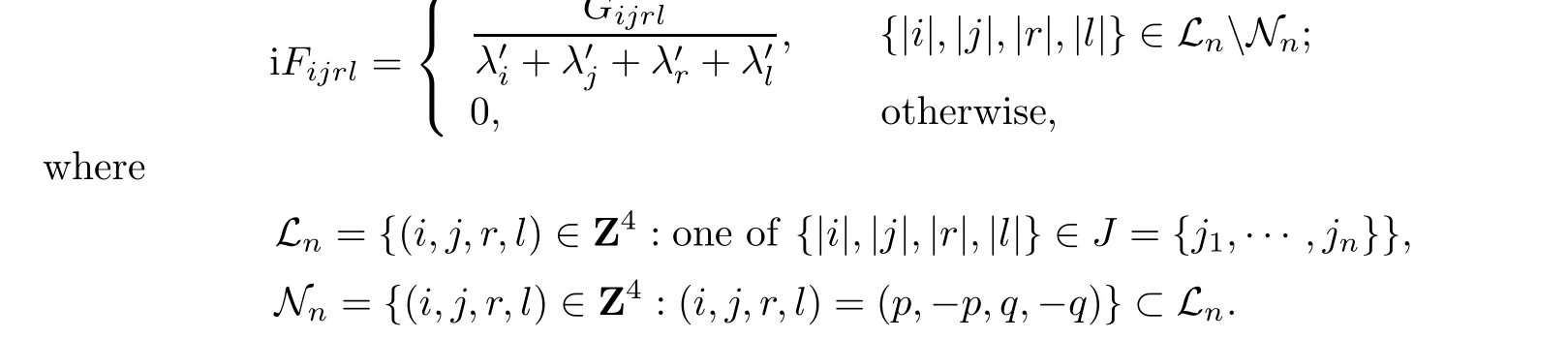
LetΓbe the time-1 map of the flow of the Hamiltonian vector field F.Expanding at t=0 and by Taylor’s formula,we obtain

To prove analyticity and regularity of the preceding transformation we first show XF: la,s→la,s+2.Indeed,by Lemma 3.4 and(3.5)with

The analyticity of Fwfollows from the analyticity of each component functions and its local boundedness.Hence in a sufficiently small neighborhood of the origin in la,sthe time-1-mapΓis well de fi ned with the estimates

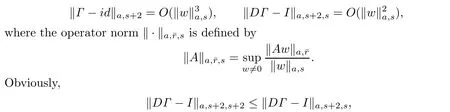
while in a sufficiently small neighborhood of the origin,DΓde fi nes an isomorphism of la,s+2. Since XH:la,s→la,s+2,we have

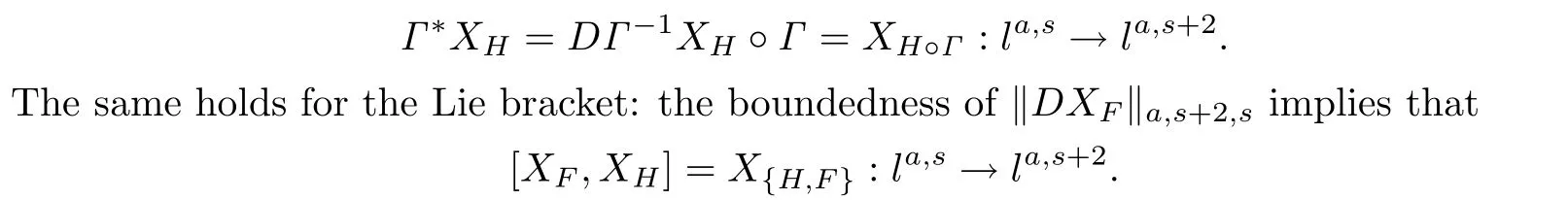
These two facts show that XK:la,s→la,s+2.The analogous claims for X¯Gand XˆGare obvious.

4 Proof of the Main Theorem

We now prove Theorem 1.1 by applying Theorems 2.1 and 2.2.In Section 3 we see that there exists a real analytic,symplectic change of coordinatesΓ,which takes H into

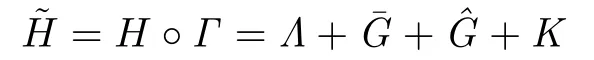
with the notation of the previous section:

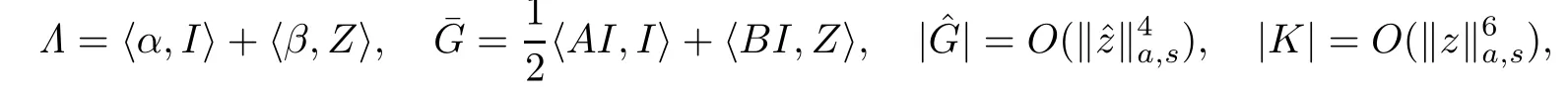
where

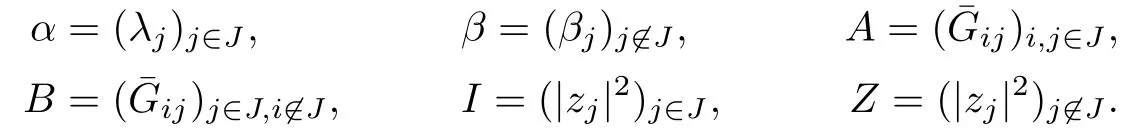
Moreover,the regularity of the nonlinear vector field is preserved.We introduce symplectic polar and real coordinates by setting

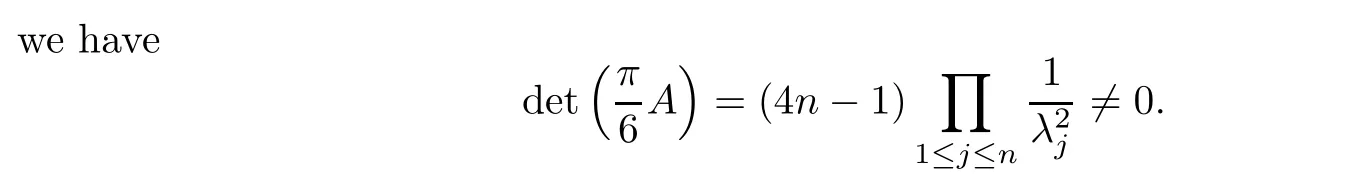
So the matrix A is non-degenerate and the map ξ→ω(ξ)is a lipeomorphism ofRnonto itself.The measure condition is satis fi ed,since hk,ω(ξ)i+hl,Ω(ξ)i is a non-trivial affine function of ξ which vanishes on a codimension 1 subspace.Finally,clearly hl,βi0,for 1≤|l|≤2,and Bξ is small because of|ξ|small and B=()j∈J,i6∈J.Then we have hl,Ω(ξ)i0 on O.So(A1)is satis fi ed.

Since

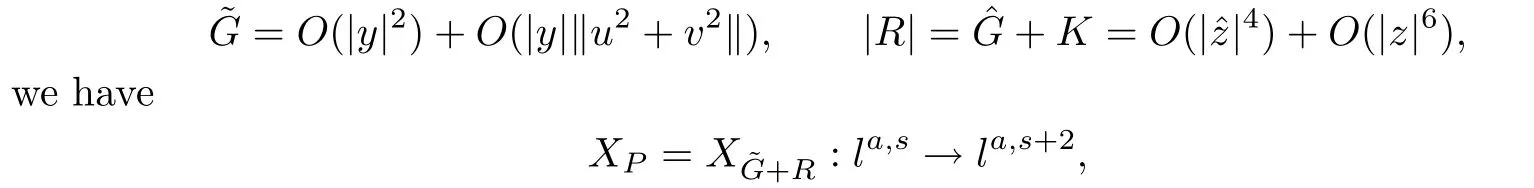
and thus,(A3)holds true with

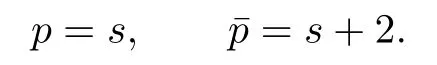
Moreover,since the frequency

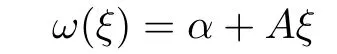
with the matrix A is invertible,we find that the condition(2.5)is satis fi ed. Finally,as in[7],we can chose γ,α such that

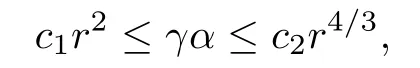
where c1,c2are constants.The Hamiltonian˜H is well de fi ned on the phase space domain

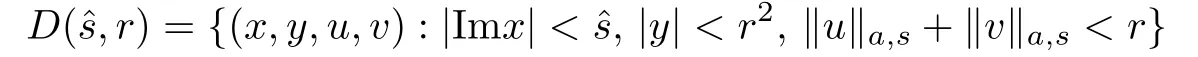
and the parameter domain

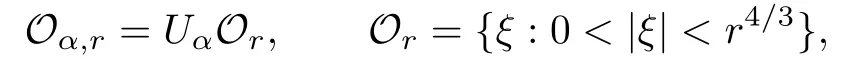
where UαOris the subset of all points in Orwith boundary distance greater than α.On these domains,we have

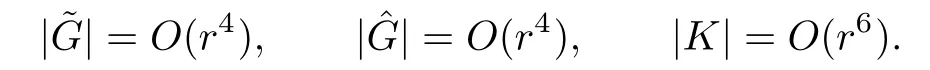
Using Cauchy estimates,we obtain

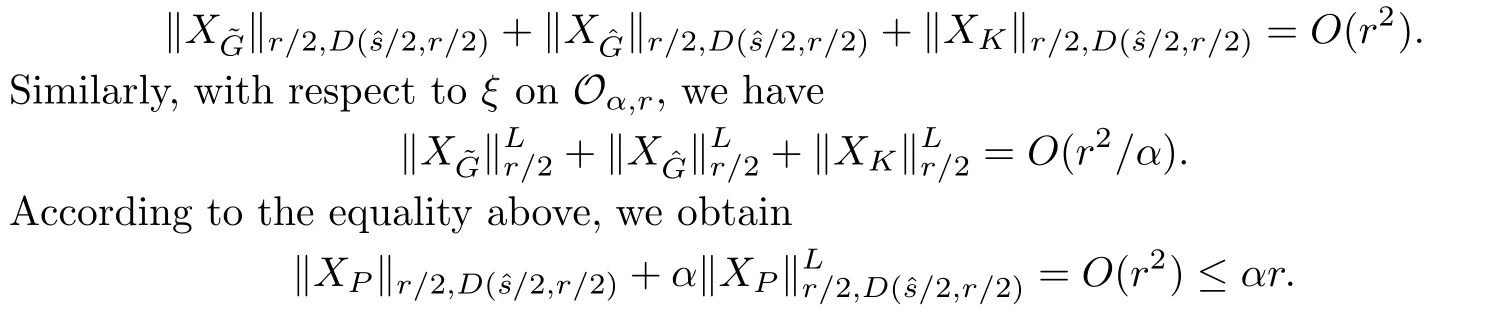
Thus the equation(2.6)holds true.

Thus,all the conditions of Theorems 2.1 and 2.2 are satis fi ed,and we finish the proof of the main theorem.

5 Appendix

Lemma 5.1Suppose thatf(m)is ann-th differentiable function on the closure¯IofI, whereI∈Ris an interval.Let

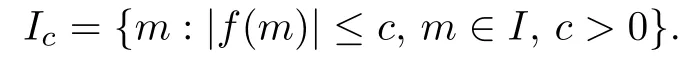
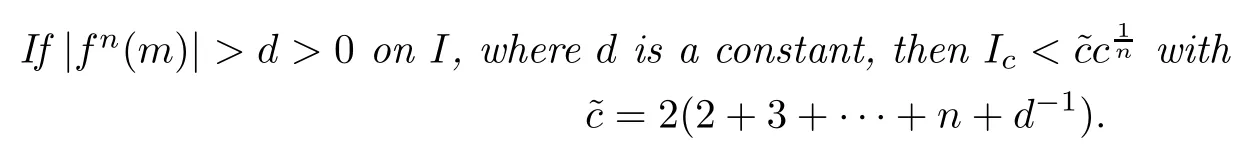
The proof can be found in[12].

[2]Chierchia L,You J.KAM tori for 1D nonlinear wave equations with periodic boundary condtions.Comm.Math.Phys.,2000,211:498–525.

[3]Eliasson L H,Kuksin S B.KAM for non-linear Schrdinger equation.Ann.of Math.,2010, 172:371–435.

[4]Gao Y,Li Y,Zhang J.Invariant tori of nonlinear Schrdinger equation.J.differential Equations,2009,246:3296–3331.

[5]Geng J,You J.A KAM theorem for one-dimensional Schrdinger equation with periodic boundary conditions.J.differential Equations,2005,209:1–56.

[6]Geng J,Yi Y.Quasi-periodic solutions in a nonlinear Schrdinger equation.J.differential Equations,2007,233:512–542.

[7]Geng J,You J.KAM tori of hamiltonian perturbations of 1D linear beam equations.J.Math. Anal.Appl.,2003,277:104–121.

[8]Yuan X.A KAM theorem with applications to partial differential equations of higher dimensions.Comm.Math.Phys.,2007,275:97–137.

[9]Kuksin S B.Nearly Integrable In finite Dimensional Hamiltonian Systems.Lecture Notes in Math.vol.1556.Berlin:Springer,1993.

[10]Wayne C E.Periodic and quasi-periodic solutions for nonlinear wave equation via KAM theory.Comm.Math.Phys.,1990,127:479–528.

[12]Xu J,You J,Qiu Q.Invariant tori for nearly integrable Hamiltonian systems with degenaracy.Math.Z.,1997,226:375–387.

Communicated by Li Yong

37K55

A

1674-5647(2012)01-0051-14

date:Dec.2,2009.

The NSF(11001042)of China,the SRFDP Grant(20100043120001)and FRFCU Grant (09QNJJ002).