Strong Converse Inequality for the Meyer-Knig and Zeller-Durrmeyer Operators∗

QI QIU-LANAND LIU JUAN

(1.College of Mathematics and Information Science,Hebei Normal University,

Shijiazhuang,050016)

(2.No.1 Middle Shcool of Handan,Handan,Hebei,056002)

Strong Converse Inequality for the Meyer-Knig and Zeller-Durrmeyer Operators∗

QI QIU-LAN1AND LIU JUAN2

(1.College of Mathematics and Information Science,Hebei Normal University,

Shijiazhuang,050016)

(2.No.1 Middle Shcool of Handan,Handan,Hebei,056002)

In this paper we give a strong converse inequality of type B in terms of uni fi ed K-functional(f,t2)(0≤λ≤1,0＜ α＜ 2)for the Meyer-Knig and Zeller-Durrmeyer type operators.

Meyer-Knig and Zeller-Durrmeyer type operator,moduli of smoothness,K-functional,strong converse inequality,Hlder’s inequality

1 Introduction

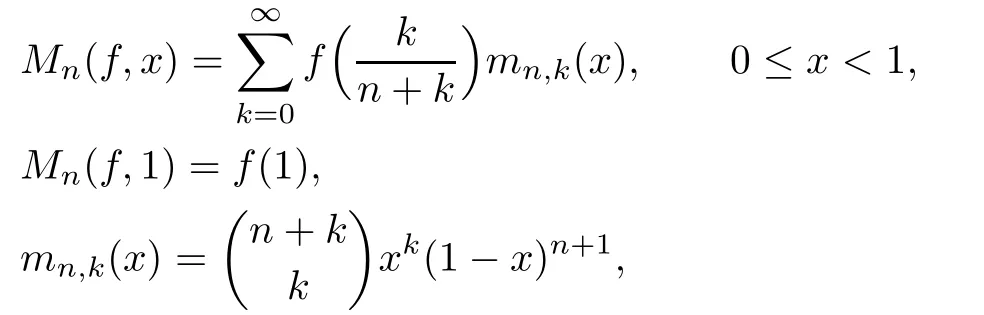
which were the object of several investigations in approximation theory(see[1–3]).In recent years there are many results of strong converse inequalities for various operators(see[4–7]).Since the expression of the moment of the Meyer-Knig and Zeller type operators is very complicated(see[8–10]),we have not seen any result of strong converse inequality for Meyer-Knig and Zeller-Durrmeyer type operators.In this paper,we study the modi fi cation of Meyer-Knig and Zeller-Durrmeyer type operators(f,x):

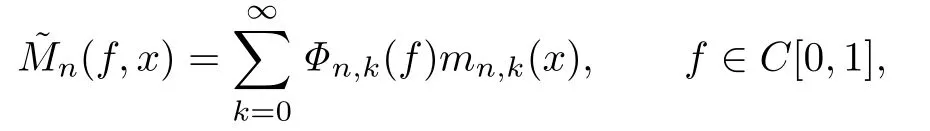
Throughout this paper,C denotes a positive constant independent of n and x,which are not necessarily the same at each occurrence.

2 Lemmas

In order to prove our main result,we need the following fundamental lemmas.Proof.Using Hlder’s inequality,(2.4)and(2.5),we can get(2.7).The methods to estimate (2.4),(2.5)and(2.6)are similar,so we only give the proof of(2.4).

First,for k≥1,n=3,by simple calculations,we can get(2.4).

Secondly,for k≥1,n≥4,one has

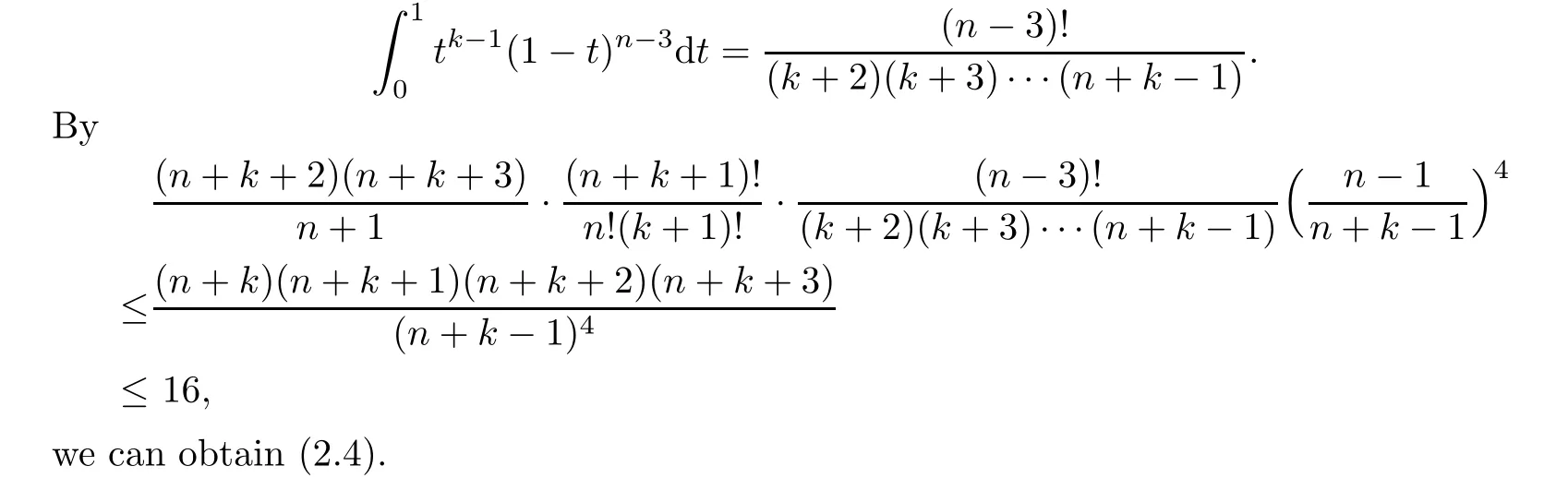
Combining the above inequality with Hlder’s inequality and Lemmas 2.2–2.4,we can get (2.11).We have thus completed the proof of Lemma 2.6.

The methods of estimating I1,I2,I3are similar,so we estimate I1for an example.It is easy to see that

3 Main Results

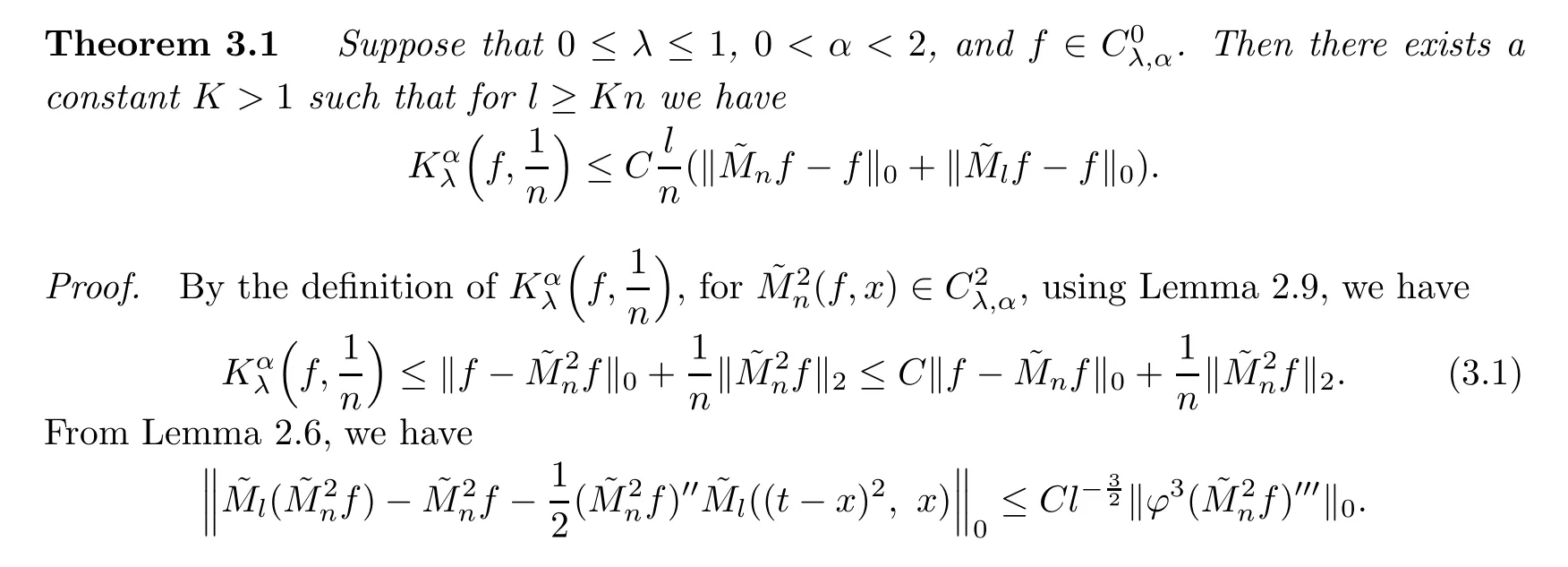
[1]Becker M,Nessel R J.A global approximation theorem for Meyer-Knig and Zeller operators.Math.Z.,1978,160:195–206.

[2]Totik V.Approximation by Meyer-Knig and Zeller operators.Math.Z.,1983,182:425–446.

[3]Totik V.Uniform approximation by Baskakov and Meyer-Knig and Zeller operators.Period. Math.Hungar.,1983,14:209–228.

[4]Chen W,Ditzian Z.Strong converse inequality for Kantorovich polynomials.Constr.Approx., 1994,10:95–106.

[5]Gonska H H,Zhou X.The strong converse inequality for Bernstein-Kantorovich operators.Comput.Math.Appl.,1995,30:103–128.

[6]Guo S,Qi Q.Strong converse inequalities for Baskakakov operators.J.Approx.Theory,2003, 124:219–231.

[7]Totik V.Strong converse inequalities.J.Approx.Theory,1994,76:369–375.

[8]Abel U.The moments for the Meyer-Knig and Zeller operators.J.Approx.Theory,1995,82: 352–361.

[9]Alkemade A H.The second moment for the Meyer-Knig and Zeller operators.J.Approx. Theory,1984,40:261–273.

[10]Guo S,Qi Q.The moments for Meyer-Knig and Zeller operators.Appl.Math.,2007,27: 719–722.

[11]Ditzian Z,Totik V.Moduli of Smoothness.New York:Springer-Verlag,1987.

Communicated by Ma Fu-ming

41A25,41A36,41A27

A

1674-5647(2012)01-0001-09

date:May 28,2007.

The NSF(10571040)of China and NSF(L2010Z02)of Hebei Normal University.