Invertible Linear Maps on the General Linear Lie Algebras Preserving Solvability∗

CHEN ZHENG-XIN AND CHEN QIONG

(School of Mathematics and Computer Science,Fujian Normal University,Fuzhou,350007)

Invertible Linear Maps on the General Linear Lie Algebras Preserving Solvability∗

CHEN ZHENG-XIN AND CHEN QIONG

(School of Mathematics and Computer Science,Fujian Normal University,Fuzhou,350007)

Let Mnbe the algebra of alln×ncomplex matrices andgl(n,C)be the general linear Lie algebra,wheren≥2.An invertible linear mapφ:gl(n,C)→gl(n,C)preserves solvability in both directions if bothφandφ−1map every solvable Lie subalgebra ofgl(n,C)to some solvable Lie subalgebra.In this paper we classify the invertible linear maps preserving solvability ongl(n,C)in both directions.As a sequence,such maps coincide with the invertible linear maps preserving commutativity on Mnin both directions.

general linear Lie algebra,solvability,automorphism of Lie algbra

1 Introduction

Let L be a Lie algebra.Recall that the derived Lie algebra L(1)of L is the Lie ideal[L,L] spanned by all[x,y],x,y∈L.To each Lie algebra L we associated the derived series:

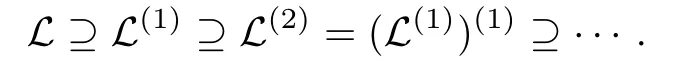
The Lie algebra L is solvable if there exists a positive integer r such that L(r)={0}.The set of all n×n complex matrices is denoted by Mnwhen considered as a set or a linear space or an algebra.If the linear space Mnis equipped with the Lie product

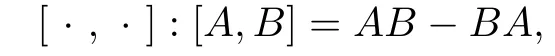
then it becomes a general linear Lie algebra,denoted by gl(n,C).

A lot of attention has been paid to linear preserver problem,which concerns the characterization of linear maps on matrix spaces or algebras that leave certain functions,subsets, relations,etc.,invariant.The earliest paper on linear preserver problem dates back to 1897 (see[1]),and a great deal of e ff ort has been devoted to the study of this type of question sincethen.One may consult the survey papers[2–4]for details.For linear or nonlinear preserver problem concerning linear Lie algebras we refer to the literature[5–12].The author in[7] characterized the invertible linear maps on simple Lie algebras of linear types preserving zero Lie products.Radjavi and Semrl in[11]characterized the nonlinear maps which preserve solvability in both directions on the general linear Lie algebras and the special linear Lie algebras.In this article we determine the invertible linear maps preserving solvability on gl(n,C)in both directions,where an invertible linear map φ:gl(n,C)→gl(n,C)is said to preserve solvability in both directions if for any solvable Lie algebra s⊆gl(n,C),both φ(s) and φ−1(s)are solvable Lie algebras of gl(n,C).Now we state our main theorem:

Theorem 1.1Letφ:gl(n,C)→gl(n,C)be an invertible linear map.The following two conditions are equivalent:

(1)φpreserves solvability in both directions;

(2)There exists a non-zero scalarµ∈C,a linear functionalfongl(n,C)withf(I)−µand an invertible matrixS∈gl(n,C)such that either

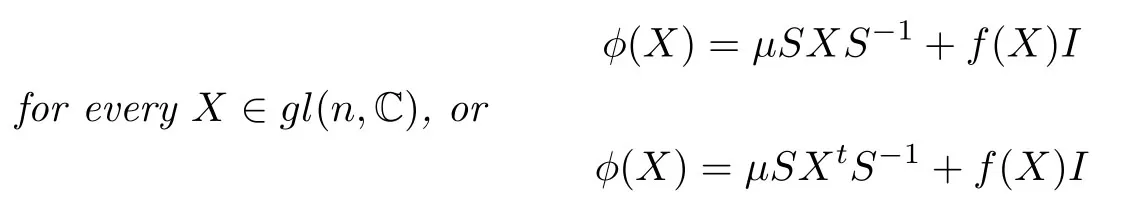
for everyX∈gl(n,C),whereXtdenotes the transpose ofX.

The above result determines an explicit form of the linear invertible map preserving solvability described in Theorem 1.1 of[11].In[12],the author proved that any bijective linear commutativity preserving map φ on Mnis also one of the above two standard maps. Thus we have the following corollary.

Corollary 1.1Letφbe an invertible linear map ongl(n,C).Then the following conditions are equivalent:

(1)φpreserves solvability in both directions;

(2)φpreserves zero Lie products in both directions.

Here we specify some notations for later use.We denote by I the identity matrix in gl(n,C)and by Eijthe matrix in gl(n,C)whose sole nonzero entry 1 is in the(i,j)-position. Let CI be the set{aI|a∈C}of all scalar matrices,H the set of all diagonal matrices in gl(n,C),andn+(resp.,n−)the set of all strictly upper(resp.,low)triangular matrices.Let D be the set of the diagonalizable matrices.Denote the one-dimensional vector space CEstby Lstfor any pair(s,t),1≤st≤n.And denote C∗=C−{0}.

2 Certain Invertible Linear Maps Preserving Solvability

In this section,we construct certain invertible linear maps preserving solvability in both directions on gl(n,C),which will be used to describe arbitrary invertible linear maps preserving solvability in both directions.

(A)Inner automorphisms:

For any invertible matrix T∈gl(n,C),the map

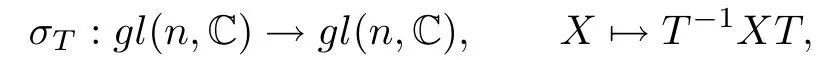
is an automorphism of gl(n,C),called an inner automorphism of gl(n,C).

(B)Graph automorphisms:

Let

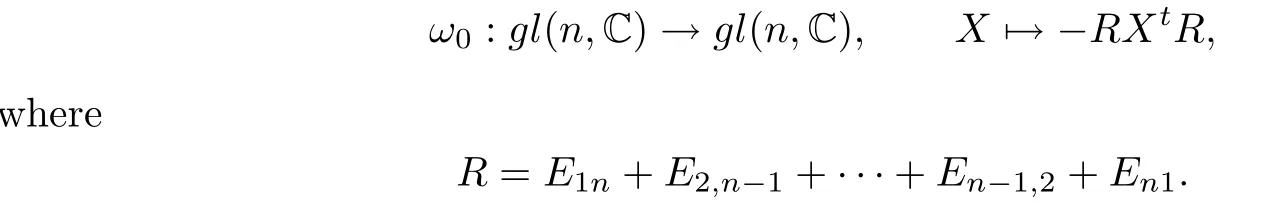
Then ω0is an automorphism of gl(n,C).Both 1 and ω0are called graph automorphism of gl(n,C).

(C)Scalar multiplication maps:

For any c∈C∗,de fi ne

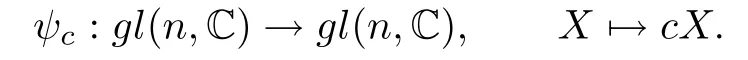
We call ψca scalar multiplication map on gl(n,C).It is obvious that any scalar multiplication map is an invertible linear map preserving solvability in both directions.

(D)Invertible linear maps induced by a linear function on gl(n,C):

Let f:gl(n,C)→C be a linear function such that

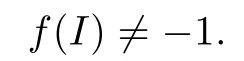
It is easy to see that the map

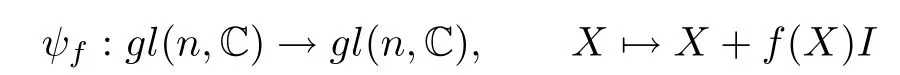
is an invertible linear map,and its inverse is the linear mapde fi ned by

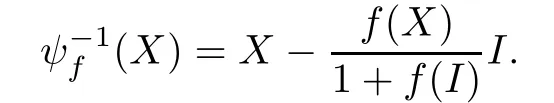
The map ψfis called an invertible linear map induced by the linear function f.Since

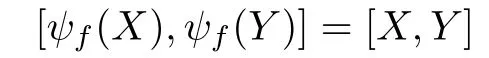
for any X,Y∈gl(n,C),ψfpreserves solvability in both directions.

The following lemma is easy to check.

Lemma 2.1(1)ψc′·ψc=ψc′cfor anyc,c′∈C∗;

(2)σT′·σT=σTT′for any pair of invertible matricesT,T′∈gl(n,C);

By Lemma 2.1 we have

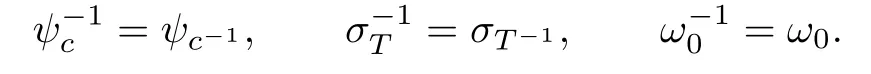
3 Proof of the Main Theorem

Before proving the main theorem,we recall some results from Theorem 1.1,Proposition 2.4 and the proof of Lemma 2.5 in[11].

Lemma 3.1Letφbe a bijective map ongl(n,C)preserving solvability in both directions. Then

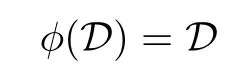
and two diagonalizable matricesAandBcommute if and only ifφ(A)andφ(B)commute. Moreover,letDk(k=1,2,···,n)be the set of all diagonalizable matrices with exactlykdistinct eigenvalues.Then we have

for some nonzeroλ∈C∗.

Proof of Theorem 1.1First we prove that Theorem 1.1 holds for n≥3.

For the sufficient direction,it is easy to see that φ is an invertible linear map and its inverse is given by

for any X,Y∈gl(n,C),for any solvable Lie subalgebra s of gl(n,C),φ(s)is a solvable Lie subalgebra of gl(n,C).Similarly,φ−1preserves solvability.Thus φ is an invertible linear map preserving solvability in both directions.

Now we prove the essential direction of the theorem.Let φ be an invertible linear map on gl(n,C)preserving solvability in both directions.First observe that the image(under φ)of a solvable subalgebra generated by a subset X of gl(n,C)is precisely the subalgebra generated by φ(X).We prove the main theorem through the following nine steps.

Step 1.There exists an invertible matrixS1∈gl(n,C)such that

For a diagonal matrix

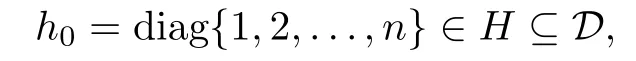
we have φ(h0)∈D by Lemma 3.1,and so there exists an invertible matrix S1∈gl(n,C) such that

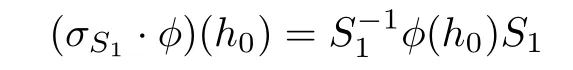
is a diagonal matrix.Denote

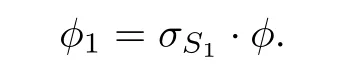
Then φ1is still an invertible linear map on gl(n,C)preserving solvability in both directions. Let

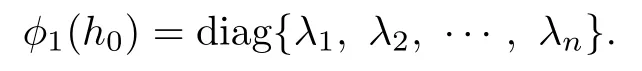
Since h0∈Dn,by Lemma 3.1,φ1(h0)∈Dn,and so

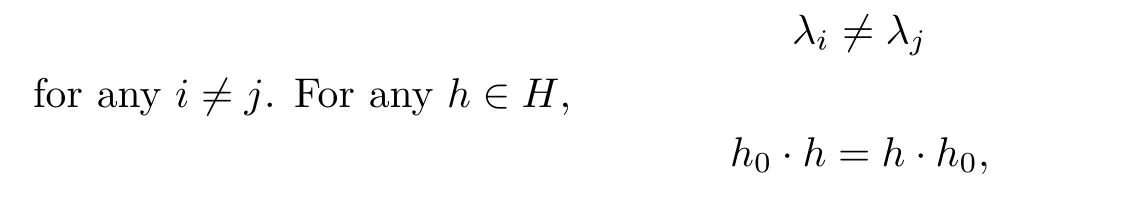
so by Lemma 3.1,

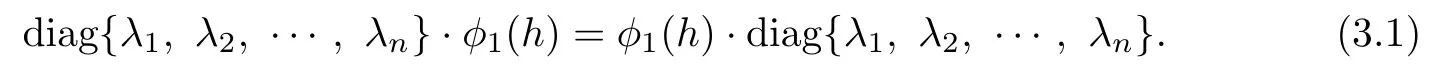
By the above equality(3.1),we know that φ1(h)is a diagonal matrix.It follows that

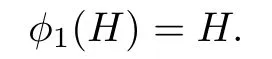
Step 2.For any pair(s,t),1≤st≤n,there exists some pair(p,q),1≤pq≤n, such that

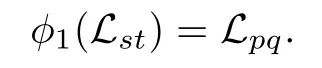
Consider φ1(H+Lst).Since H+Lstis an(n+1)-dimensional solvable subalgebra containing H,φ1(H+Lst)is also an(n+1)-dimensional solvable subalgebra containing H. First we prove that

Applying(ad h1)repeatedly on x,we have

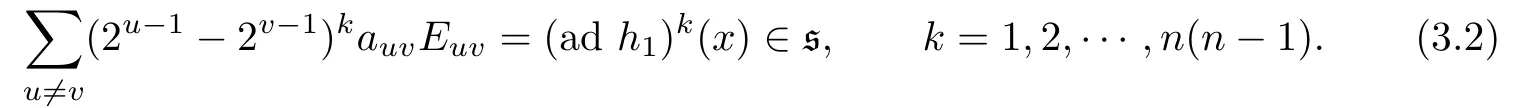
View the above equations(3.2)as a system of linear equations in n2−n variants(2u−1−2v−1)auvEuvfor the pairs(u,v)with coefficients(2u−1−2v−1)k−1.For any(u,v)(u′,v′), it is easy to see that

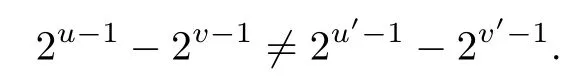
So the determinant of coefficients of variants(2u−1−2v−1)auvEuv,being exactly a Vandermonde determinant,takes a nonzero value.So each(2u−1−2v−1)auvEuvcan be written as a linear combination of

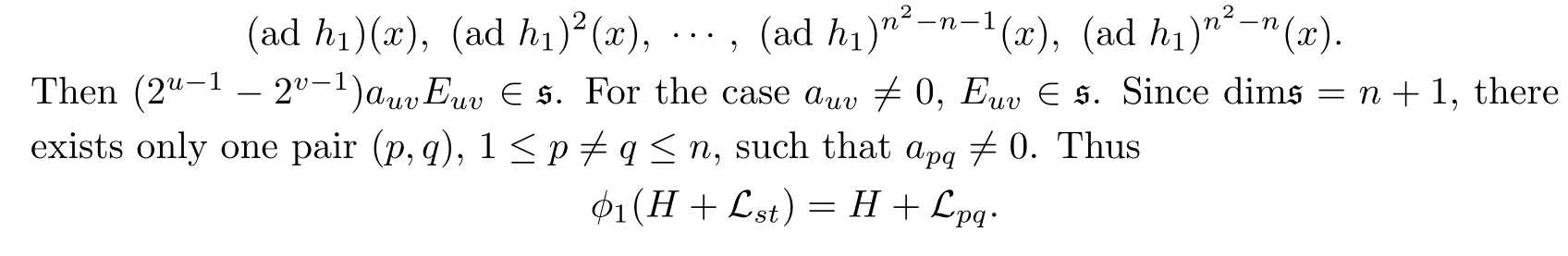
Assume that

where h∈H,a∈C∗.We now need to show that h=0.Otherwise,take

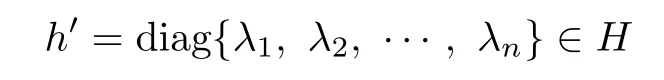
such that

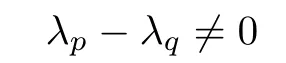
and h′,h are linearly independent(do exist).Let

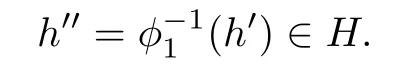
Since Lst+Ch′′is a two-dimensional solvable subalgebra generated by Estand h′′,φ1(Lst+ Ch′′)is a two-dimensional solvable subalgebra generated by aEpq+h and h′.By

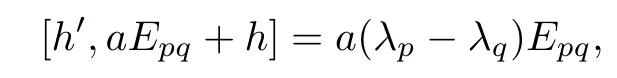
we see that h=0.Thus

Step 3.There exists some invertible matrixS2such that

(1)(φ1·σS2)(H)=H;

(2)(φ1·σS2)(Lst)⊆n+for any1≤s＜t≤n;

(3)(φ1·σS2)(Lst)⊆n−for any1≤t＜s≤n.

It is not difficult to see that(2)is equivalent to the following announcement:

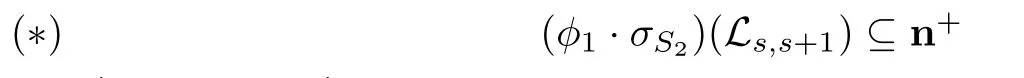
for any 1≤s≤n−1.

Since(3)follows from(2)by Step 2,we only need to prove(1)and(∗).

Let

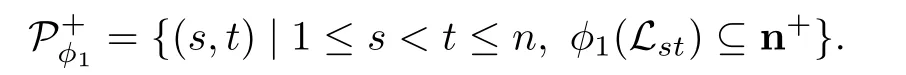
Now we use decreasing induction on Cardto complete(1)and(∗).If

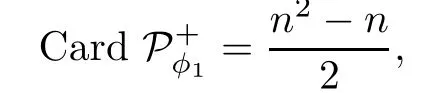
i.e.,φ1(Lst)⊆n+for any 1≤s＜t≤n,then we choose S2=I to complete the proof.If

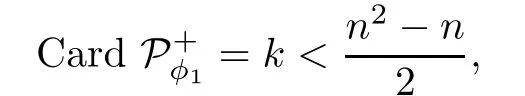
then there exists at least one i∈{1,2,···,n−1}such that φ1(Li,i+1)⊆n−.Choose an invertible matrix

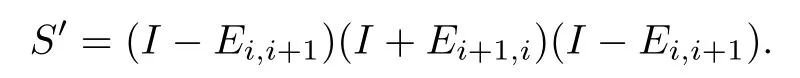
By an easy computation,we have the following results:

(i)σS′(diag{a1,···,ai,ai+1,···,an})=diag{a1,···,ai+1,ai,···,an},and so

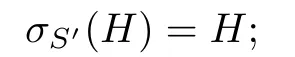
(ii)σS′(Ei,i+1)=−Ei+1,i,and so

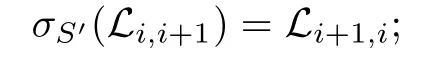
(iii)For any t＞i+1,

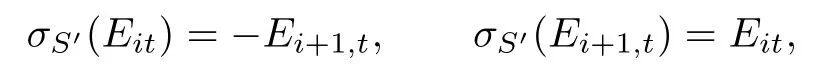
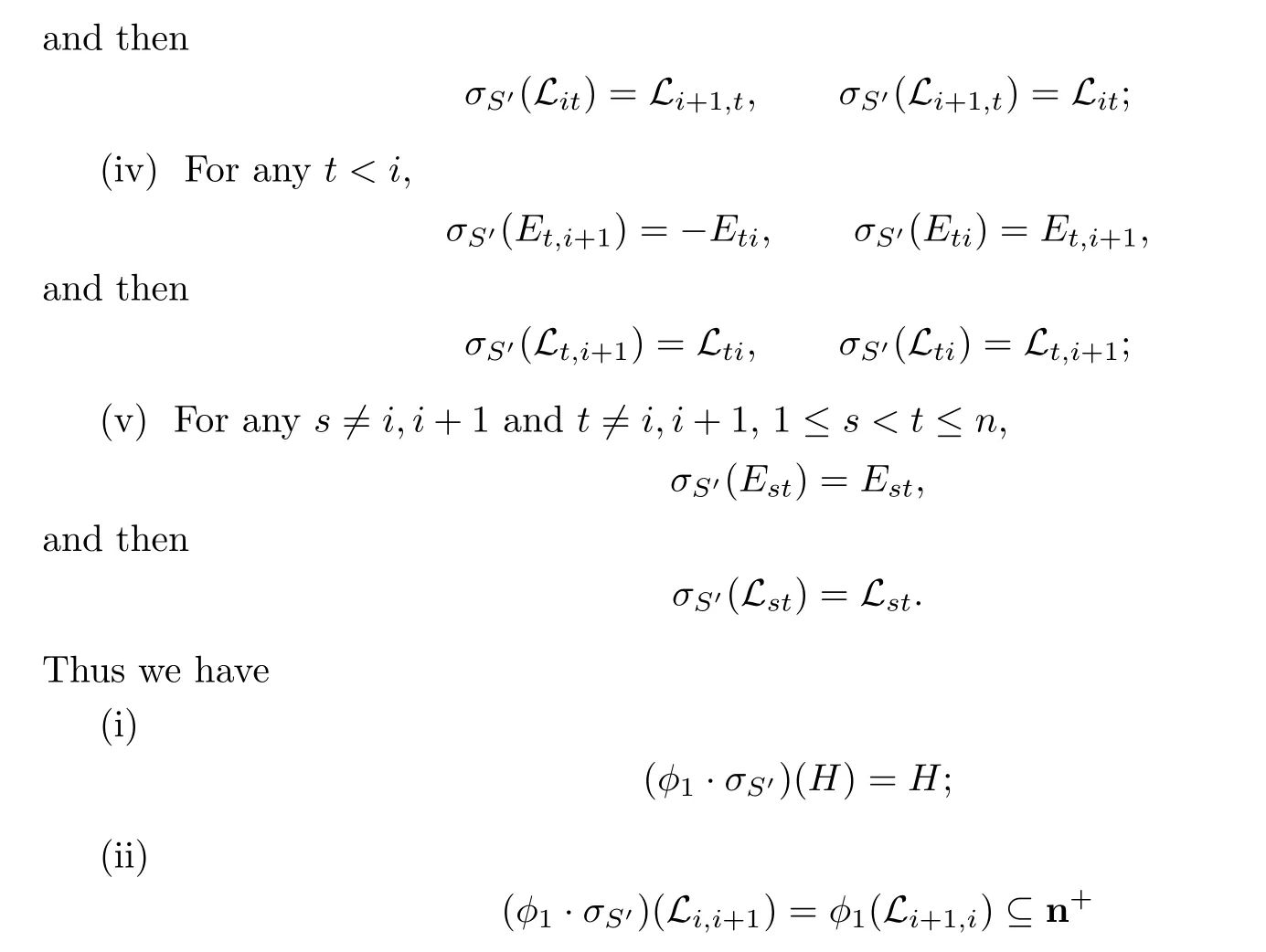
(if φ1(Li+1,i)⊆n−,then φ1(Li,i+1+H+Li+1,i)=H+φ1(Li,i+1)+φ1(Li+1,i)⊆H+n−is solvable,which contradicts the fact that Li,i+1+H+Li+1,iis not solvable);

(iii)φ1·σS′induces a permutation on the set{Lst|(s,t)(i,i+1),1≤s＜t≤n}. One will see that the number of pairs(s,t),1≤s＜t≤n,satisfying that

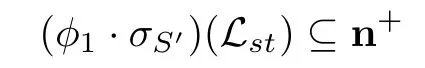
is precisely k+1.By induction hypotheses,there exists an invertible matrix S′′such that

(i)((φ1·σS′)·σS′′)(H)=H;

(ii)((φ1·σS′)·σS′′)(Lst)⊆n+for any 1≤s＜t≤n.

Let

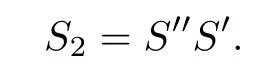
Then by Lemma 2.1(2),the proofs of(1)and(2)are completed.

In the remainder of this proof,we denote

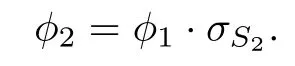
Step 4.For anys∈{1,2,···,n−1},there is somej∈{1,2,···,n−1}such that

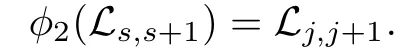
By Step 3,

Since dimφ2(n+)=dimn+,we have

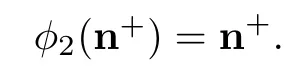
Sincen+is a solvable subalgebra generated by all Ls,s+1for s∈{1,2,···,n−1},we see thatn+is also generated by all φ2(Ls,s+1)for s∈{1,2,···,n−1}.Then Step 4 holds from Step 2.

Step 5.There is a graph automorphismωofgl(n,C)such that

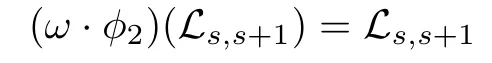
for anys∈{1,2,···,n−1}.

For any two distinct s,t∈{1,2,···,n−1},|s−t|=1 if and only if the dimension of the solvable subalgebra generated by Ls,s+1and Lt,t+1is 3,and|s−t|＞1 if and only if the dimension of the solvable subalgebra generated by Ls,s+1and Lt,t+1is 2.By Step 4,we can set π to be the permutation of{1,2,···,n−1}such that

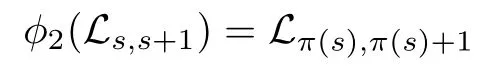
for any s=1,2,···,n−1.Since the dimension of the solvable subalgebra generated by Ls,s+1and Lt,t+1is equal to the dimension of the solvable subalgebra generated by Lπ(s),π(s)+1and Lπ(t),π(t)+1,|s−t|=1 if and only if|π(s)−π(t)|=1,and|s−t|＞1 if and only if |π(s)−π(t)|＞1.Then either

(1)π(s)=s,1≤s≤n−1,or

(2)π(s)=n−s,1≤s≤n−1.

For the case(1),we set ω=I;and for the case(2),we set ω=ω0.Then Step 5 holds.

Denote

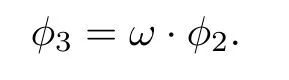
Step 6.φ3(Lst)=Lstfor anys,t∈{1,2,···,n}andst.

At first we prove that

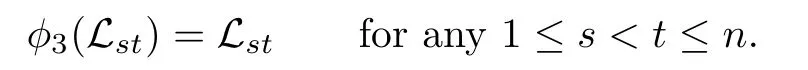
To achieve the aim we use decreasing induction on t−s,where 1≤t−s≤n−1.For t−s=n−1,then t=n,s=1.Since L1n+Lk,k+1is a two-dimensional solvable subalgebra for any k=1,2,···,n−1,the image φ3(L1n+Lk,k+1)is also a two-dimensional subalgebra, which is generated by φ3(L1n)and φ3(Lk,k+1).Assume that

Then there is some i∈{1,2,···,n−1}such that

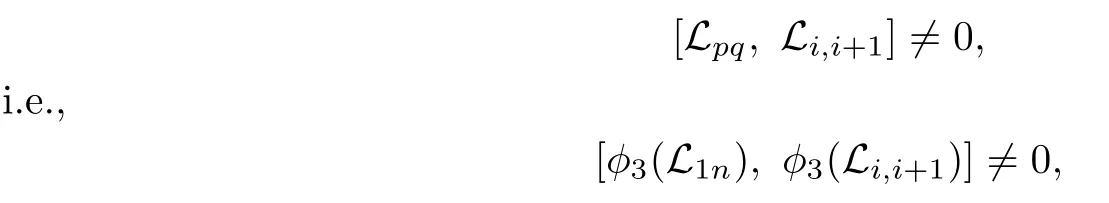
which implies that the subalgebra of gl(n,C)generated by φ3(L1n)and φ3(Li,i+1)is at least three-dimensional,a contradiction.Thus

for any pair(s,t)satisfying t−s≥k+1,1≤s＜t≤n.Let(p,q)be a pair satisfying |p−q|=k and 1≤p＜q≤n.There is some i∈{1,2,···,n−1}such that

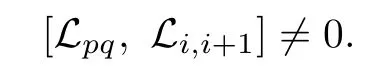
The subalgebra t generated by Lpqand Li,i+1is

which is three-dimensional and solvable.We consider the three-dimensional solvable algebra φ3(t).On the one hand,it is the subalgebra generated by φ3(Lpq)and Li,i+1,i.e.,it is the subalgebra

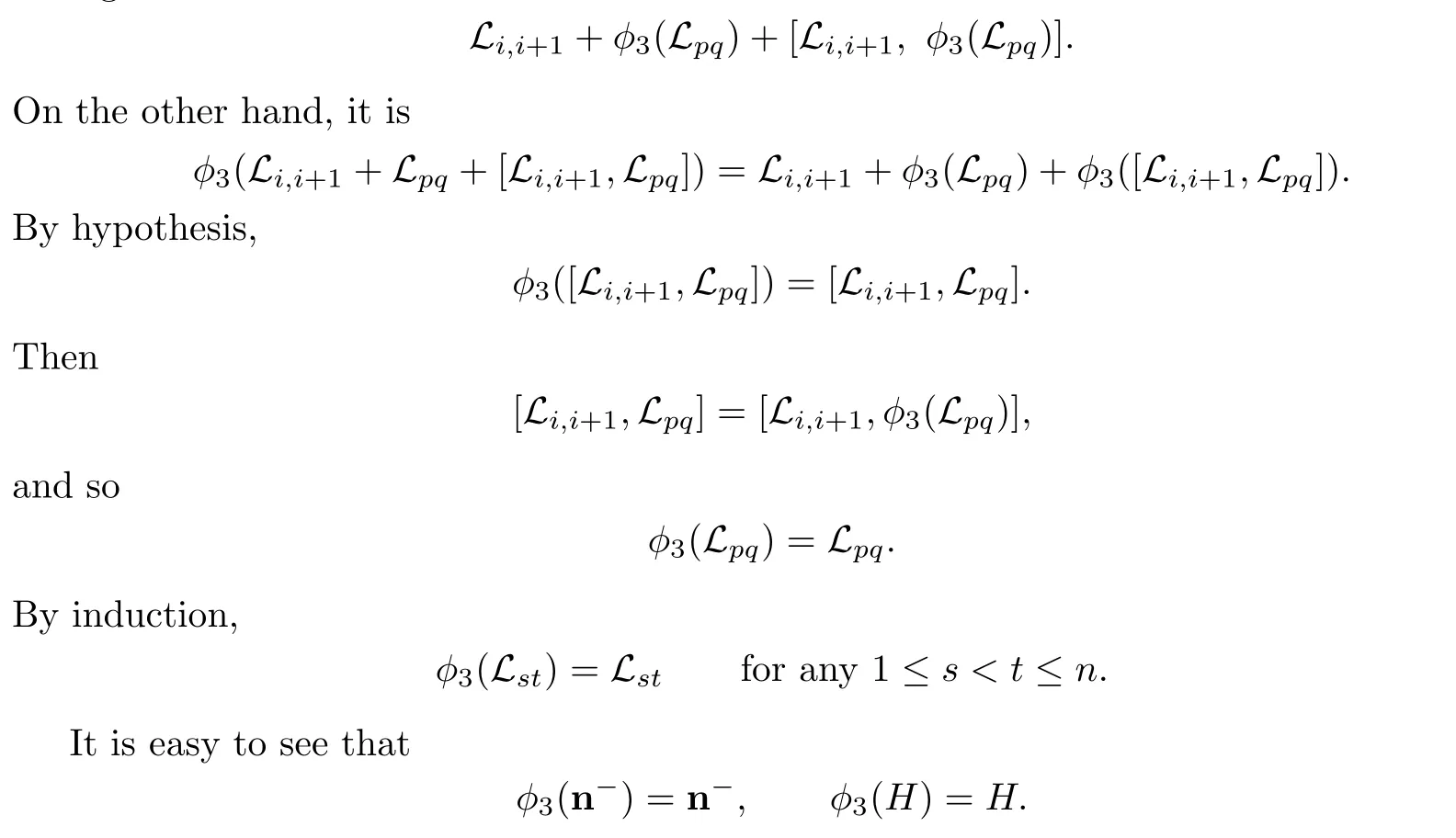
As in Step 4,we can similarly prove that for any 1≤i≤n−1,there is some j such that

For a given i∈{1,2,···,n−1},if the above ji,then the solvability of Lj+1,j+Li,i+1+H will force

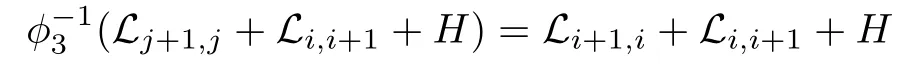
to be solvable,absurd.So

A similar discussion to the above shows that

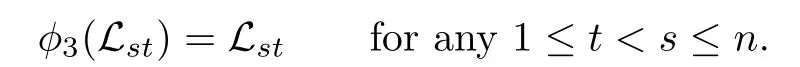
Step 7.There exist a constantv∈C∗and a linear functionf′such that

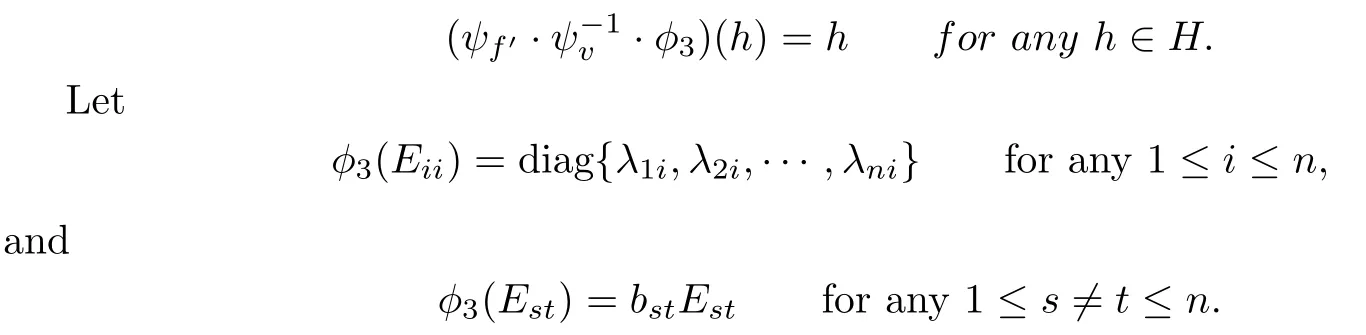
For any fixed i∈{1,2,···,n},and any two distinct j,ki,Eiiand Ejk+Ekjgenerate a two-dimensional solvable subalgebra of gl(n,C).So φ3(Eii)and φ3(Ekj+Ejk)also generate a two-dimensional subalgebra of gl(n,C).Since

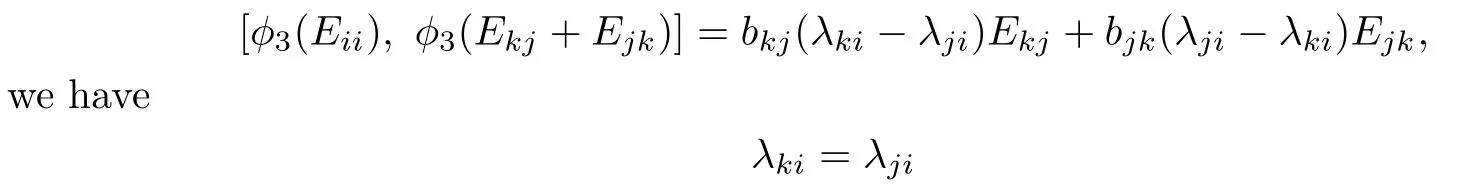
Denote

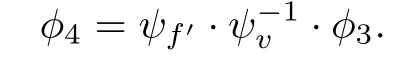
Step 8.There is an invertible matrixS3such that

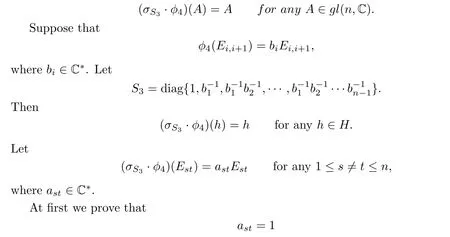
for any pair(s,t)such that 1≤s＜t≤n by induction on t−s.It is easy to check that

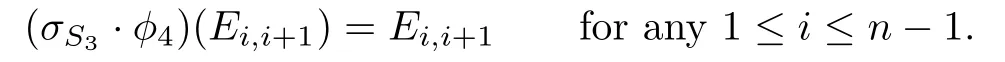
So it holds for t−s=1.Assume that

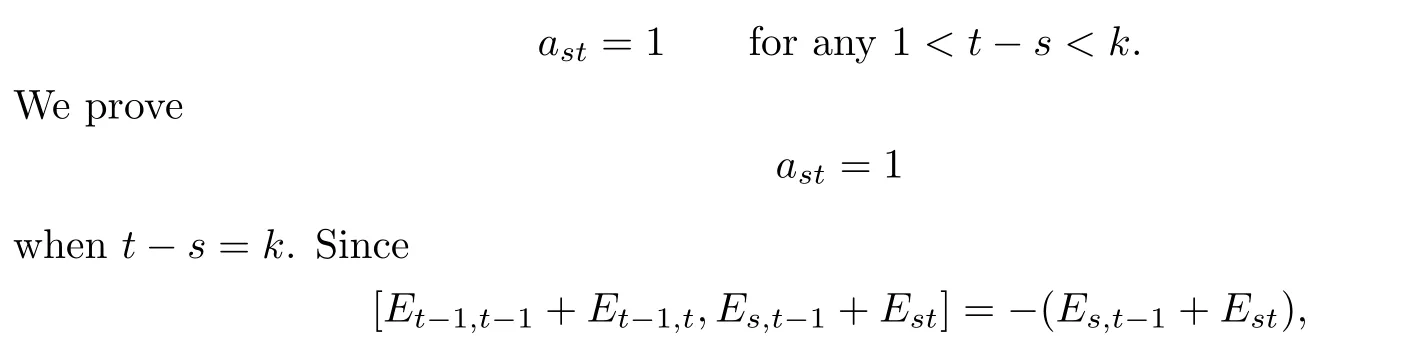
Et−1,t−1+Et−1,tand Es,t−1+Estgenerate a two-dimensional solvable subalgebra,and so (σS3·φ4)(Et−1,t−1+Et−1,t)and(σS3·φ4)(Es,t−1+Est)also generate a two-dimensional solvable subalgebra,where

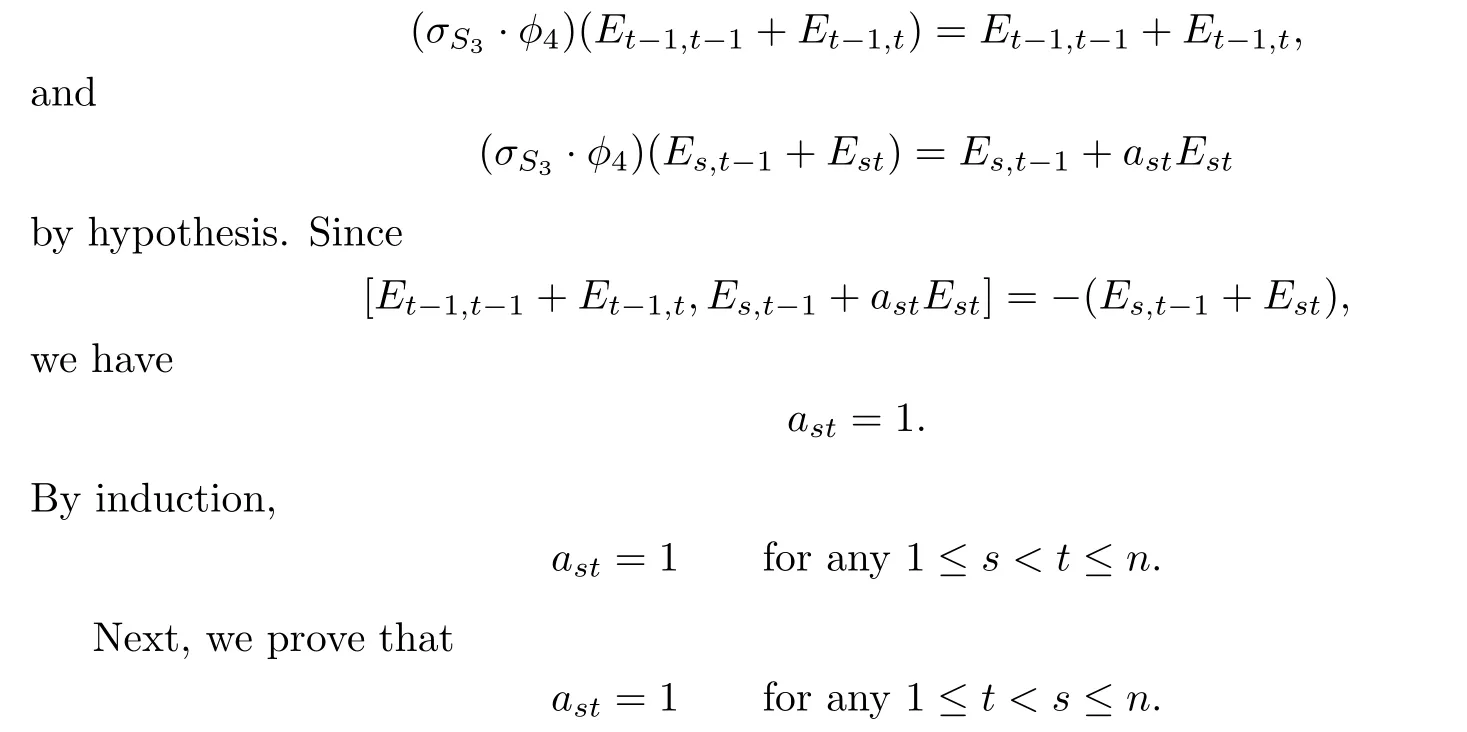
First we prove that

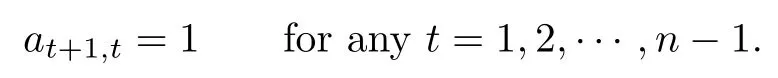
We prove it in the following two cases.

Case 1.t=1.

Since

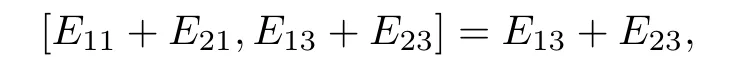
we see that E11+E21and E13+E23generate a two-dimensional solvable subalgebra of gl(n,C),and so(σS3·φ4)(E11+E21)and(σS3·φ4)(E13+E23)also generate a two-dimensional subalgebra of gl(n,C).SinceCase 2.t＞1.

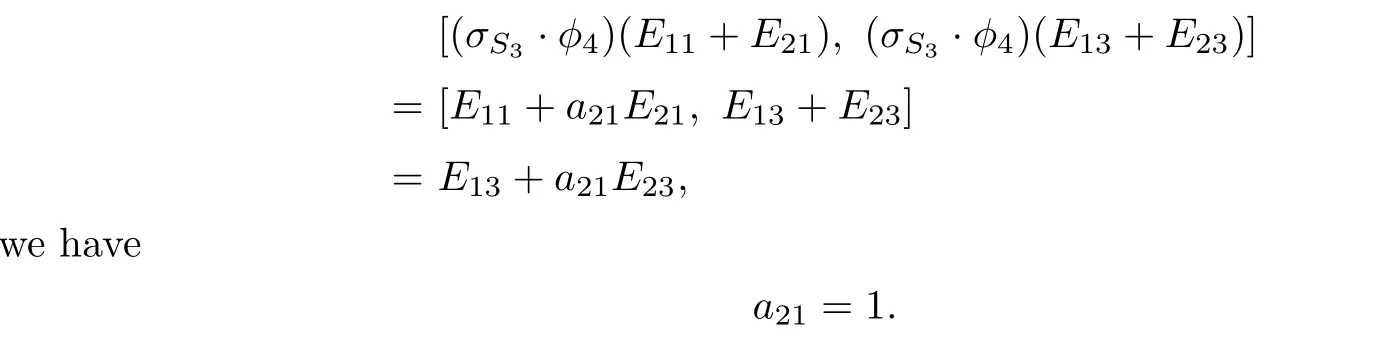
Since

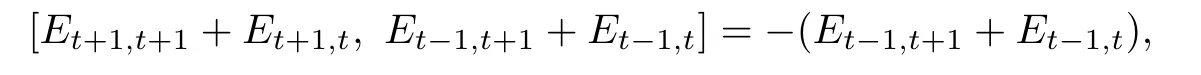
we see that Et+1,t+1+Et+1,tand Et−1,t+1+Et−1,tgenerate a two-dimensional solvable subalgebra of gl(n,C),and so(σS3·φ4)(Et+1,t+1+Et+1,t)and(σS3·φ4)(Et−1,t+1+Et−1,t) also generate a two-dimensional solvable subalgebra of gl(n,C).Since

A similar discussion as above shows that

Thus Step 8 holds.

Step 9.There are a nonzero elementµ∈C∗,an invertible matrixSand a linear functionfongl(n,C)withf(I)−µsuch that either

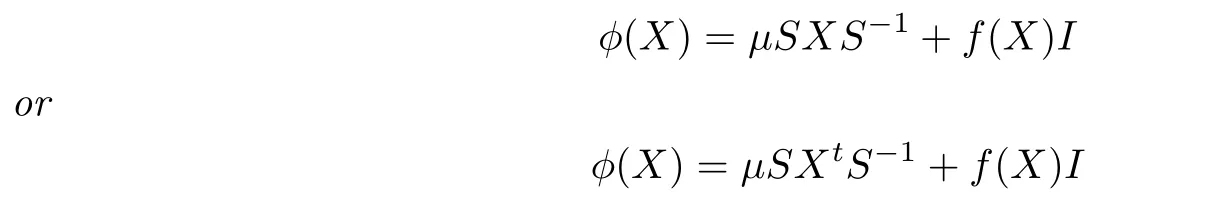
for anyX∈gl(n,C).

By Step 8,

and so

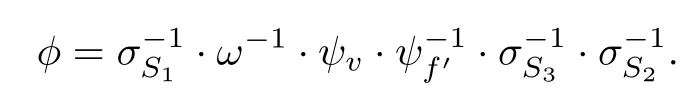
We prove Step 9 in the following two cases:

Case 1.ω=1.

In this case,by Lemma 2.1,we have

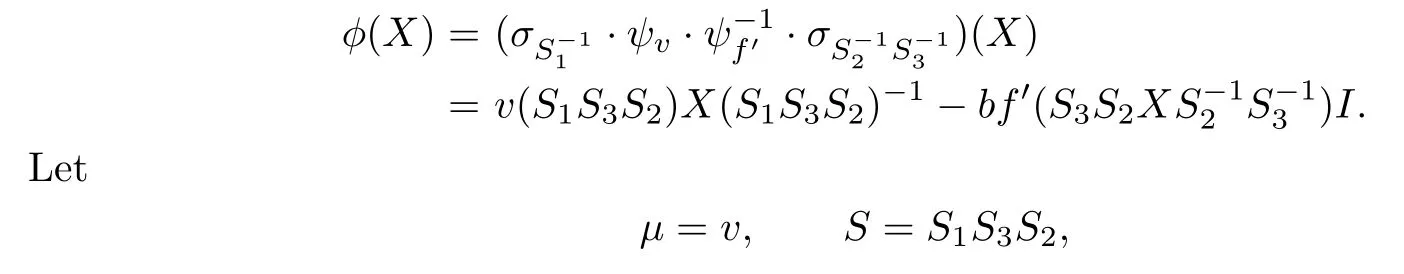
and f be the linear function determined by

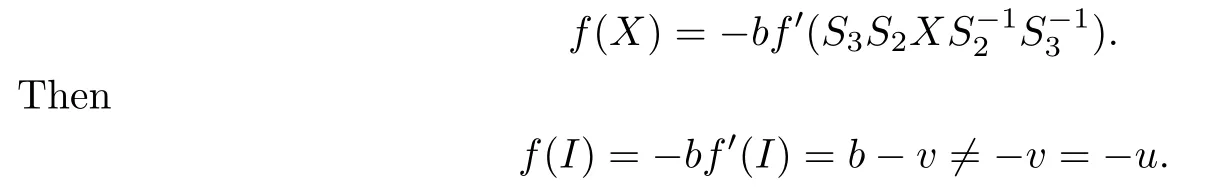
Thus Step 9 holds.

Case 2.ω=ω0.

In this case,by Lemma 2.1,we have

Thus Step 9 holds.

Finally,Theorem 1.1 holds for the case n≥3.

Next we prove Theorem 1.1 holds for n=2.

We only need to prove the essential direction.

Let φ be an invertible linear map preserving solvability on gl(2,C).

Since

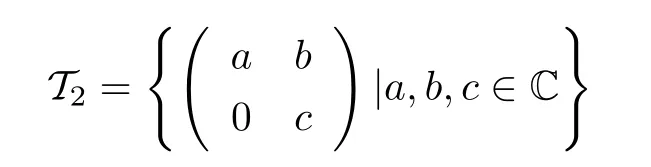
is a solvable subalgebra of gl(2,C),φ(T2)is a solvable subalgebra of gl(2,C),and so there is an invertible matrix S1such that

Here σS1·φ is still an invertible linear map preserving solvability on gl(2,C).The set gl(2,C) is a disjoint union of CI,N and D′,where N is the set of all matrices of the form λI+N with N0 and N2=0,and D′is the set of all nonscalar diagonalizable matrices.By Section 3 of[11],each of the sets CI,N,and D′is invariant under σS1·φ.Let

Since E11,E12generate a two-dimensional solvable subalgebra,φ1(E11)and φ1(E12)also generate a two-dimensional solvable subalgebra.By computation,

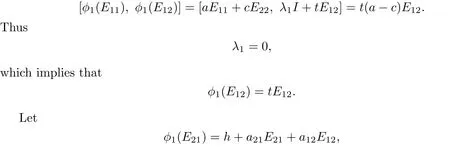
where h∈H,a12,a21∈C.Since E11,E22,E21generate a three-dimensional solvable subalgebra,φ1(E11),φ1(E22)and φ1(E21)generate a three-dimensional solvable subalgebra, denoted by t.Choose

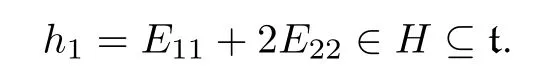
Then(ad h1)(φ1(E21))∈t,(ad h1)2(φ1(E21))∈t,i.e.,a21E21−a12E12∈t,a21E21+ a12E12∈t.Thus a21E21∈t,a12E12∈t.If a120(resp.,a210),then E12∈t(resp., E21∈t).Thus one of a12,a21is zero and the other is nonzero.Assume that

In this case φ1(E12),φ1(E21)and φ1(E11−E22)generate a solvable subalgebra of gl(2,C), which contradicts the fact that the subalgebra generated by E21,E12and E11−E22is not solvable.Thus

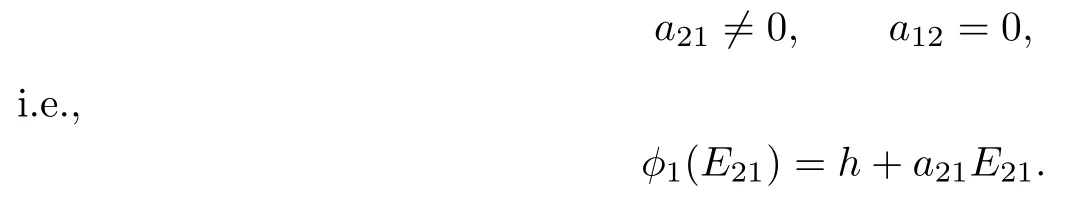
Next we prove that h=0.

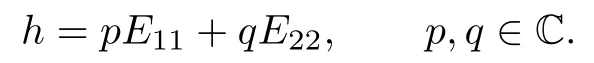
We could choose p′,q′∈C so that p′q′,and p′qq′p.Then p′E11+q′E22and h are linearly independent.Let

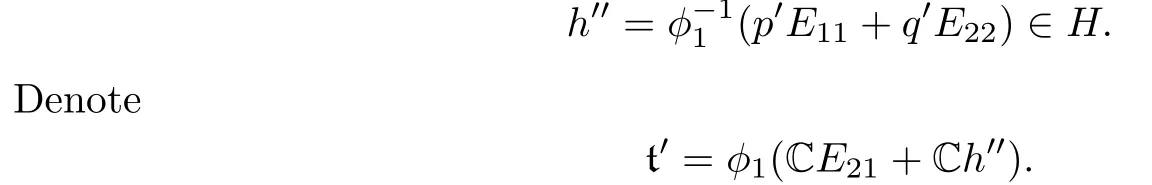
Since CE21+Ch′′is a two-dimensional solvable subalgebra generated by h′′and E21,t′is a two-dimensional solvable subalgebra generated by φ1(E21)and φ1(h′′).However,

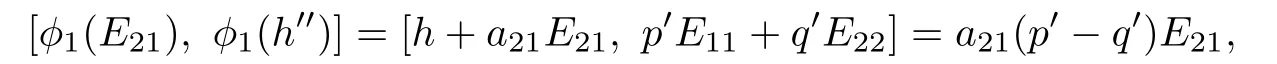
a contradiction.Thus

where a21∈C∗.So

Let f′be a linear function on C determined by

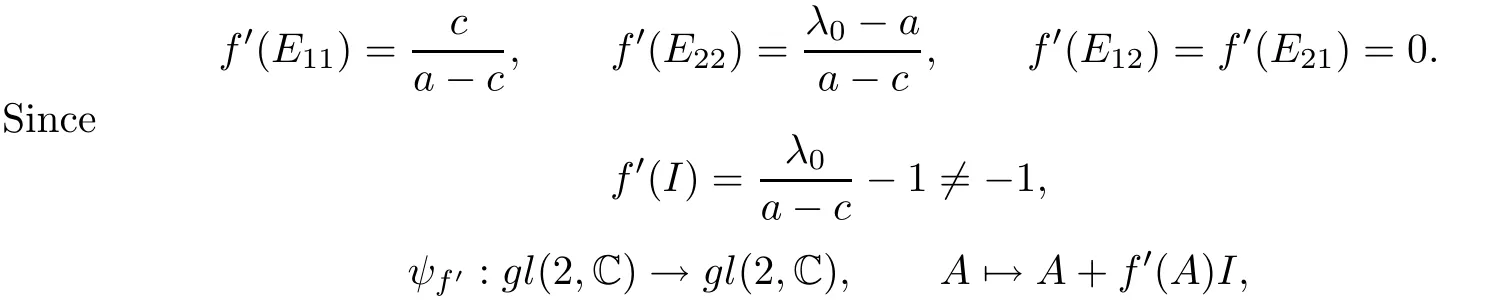
is an invertible linear map preserving solvability.It is easy to check that

we see that E11+E12−E21−E22and E21+E12generate a two-dimensional solvable subalgebra of gl(2,C),and so(σS3·φ2)(E11+E12−E21−E22)and(σS3·φ2)(E21+E12) also generate a two-dimensional solvable subalgebra of gl(2,C).By computation,

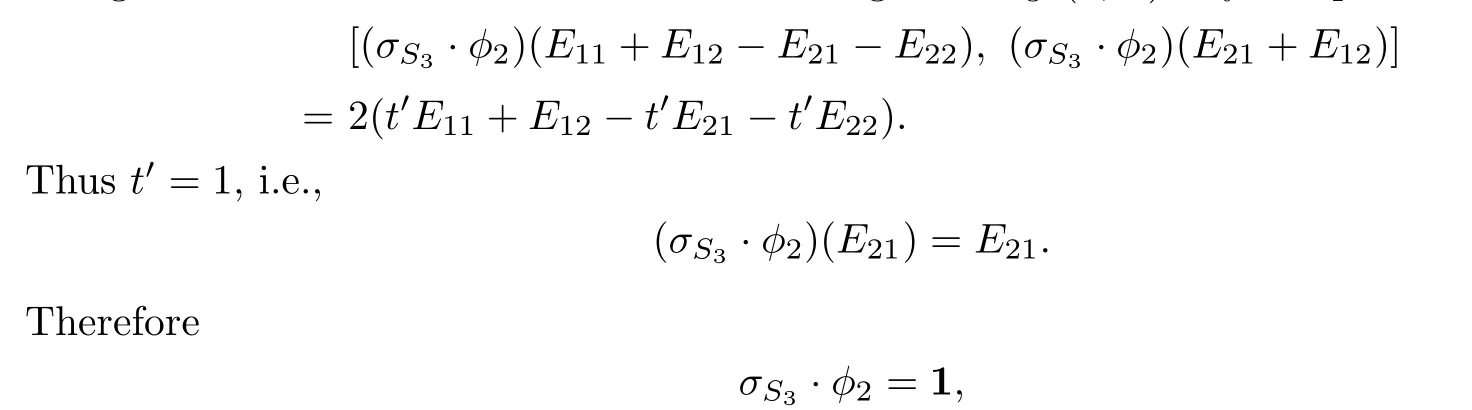
and Theorem 1.1 holds for n=2.

The proof of Theorem 1.1 is completed.

[1]Frobenius C.Uber die Darstellung der Endlichen Gruppen Durch Lineare Substitutioen.Berlin: Sitzungsber Deutsch Akad Wiss,1897.

[2]Li C K,Tsing N K.Linear preserver problem:a brief introduction and some special techniques.Linear Algebra Appl.,1992,162-164:217–235.

[3]Pierce S,Li C K,Loewy R,Lim M H,Tsing N.A survey of linear preserver problems.Linear and Multilinear Algebra,1992,33:1–129.

[4]Li C K,Pierce S.Linear preserver problem.Amer.Math.Monthly,2001,108:591–605.

[5]Marcus M.Linear operations of matrices.Amer.Math.Monthly,1962,69:837–847.

[6]Marcoux L W,Sourour A R.Commutativity preserving linear maps and Lie automorphisms of triangular matrix algebras.Linear Algebra Appl.,1999,288:89–104.

[7]Wong W J.Maps on simple algebras preserving zero products,II:Lie algebras of linear type.Paci fi c J.Math.,1981,92:469–487.

[8]Semrl P.Non-linear commutativity preserving maps.Acta Sci.Math.(Szeged),2005,71:781–819.

[9]Fosner A.Non-linear commutativity preserving maps on Mn(R).Linear and Multilinear Algebra,2005,53:323–344.

[10]Semrl P.Commutativity preserving maps.Linear Algebra Appl.,2008,429:1051–1070.

[11]Radjavi H,Semrl P.Non-linear maps preserving solvability.J.Algebra,2004,280:624–634.

[12]Watkins W.Linear maps that preserve commuting pairs of matrices.Linear Algebra Appl., 1976,14:29–35.

Communicated by Du Xian-kun

15A01,17B40

A

1674-5647(2012)01-0026-17

date:June 4,2010.

The NSF(2009J05005)of Fujian Province and a Key Project of Fujian Provincial Universities—Information Technology Research Based on Mathematics.