Uniquely Strongly Clean Group Rings∗

WANG XIU-LAN

(Department of Mathematics,Harbin Institute of Technology,Harbin,150001)

Uniquely Strongly Clean Group Rings∗

WANG XIU-LAN

(Department of Mathematics,Harbin Institute of Technology,Harbin,150001)

A ring R is called clean if every element is the sum of an idempotent and a unit,and R is called uniquely strongly clean(USC for short)if every element is uniquely the sum of an idempotent and a unit that commute.In this article,some conditions on a ring R and a group G such that RG is clean are given.It is also shown that if G is a locally finite group,then the group ring RG is USC if and only if R is USC,and G is a 2-group.The left uniquely exchange group ring,as a middle ring of the uniquely clean ring and the USC ring,does not possess this property,and so does the uniquely exchange group ring.

clean ring,group ring,p-group,USC ring

1 Introduction

In this paper,R is an associative ring with identity 1.A ring R is called clean if every element is the sum of an idempotent and a unit.This de fi nition first appeared in the paper by Nicholson[1]in 1977,in which it was also proved that clean rings are exchange rings,i.e., a ring R is exchange if and only if for any x∈R,there exists e2=e∈R such that e∈Rx and 1−e∈R(1−x).And the two concepts are equivalent for rings with all idempotents central.A ring R is called uniquely clean if each element has a unique representation as the sum of an idempotent and a unit.For instance,every boolean ring is uniquely clean, and a homomorphic image of a uniquely clean ring is uniquely clean.Uniquely clean rings were discussed in[2–4].Nicholson and Zhou[3]proved that a ring R is uniquely clean if and only if R modulo its Jacobson radical J(R)is boolean,idempotents lift modulo J(R),and idempotents in R are central if and only if for every a∈R there exists a unique idempotent e∈R such that e−a∈J(R).A ring R is called strongly clean if every element of R is the sum of an idempotent and a unit that commute.Strongly clean rings were introduced by Nicholson[5].Recently,Chenet al.[6]raised a new concept about uniquenly strongly clean(USC for short)ring.They called a ring R USC if every element is uniquely the sum of an idempotent and a unit that commute.They also gave the equivalent condition for USC ring,that is,a ring R is USC if and only if for all a∈R there exists a unique idempotent e∈R such that ea=ae and e−a∈J(R).Nicholson and Zhou[3],Chenet al.[6]proved the following results which we can use in this paper:

(1) If R is uniquely clean,then R/J(R)is boolean,and 2∈J(R);

(2) If R is USC,then R/J(R)is boolean,and 2∈J(R).

We denote by RG the group ring of G over R.The augmentation mapping

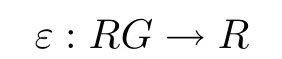
is given by

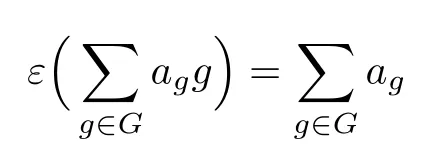
and its kernel,denoted by∆(G)(or by∆RG),is an ideal generated by{1−g,g∈G}.If H is a subgroup of G,then εH denotes the right ideal of RG generated by{1−h,h∈H}. If H is a normal subgroup of G,then εH is an ideal and RG/εH～=R(G/H).If I is a right ideal of R,then IG denotes the elements of RG with coefficients in I,when I is an ideal so is IG,and RG/IG～=(R/I)G.For further details see[7].

Three years ago,Chenet al.[8]raised a question:if R is a ring and G is a group,when is the group ring RG clean?Wang[9]studied the cleanness of group rings for a class of Abelian p-groups.But we know that Z(3)S3is a clean group ring,where S3is not Abelian.This motivates us to look at the cleanness of group rings of Abelian or non-Abelian groups.In Section 2,some conditions on a ring R and a group G such that RG is clean are given. Moreover,in Sections 3 and 4 it is shown that if G is a locally finite group,then the group ring RG is USC if and only if R is USC,and G is a 2-group.The left uniquely exchange group ring,as a middle ring of the uniquely clean ring and the USC ring,does not possess this property,and so does the uniquely exchange group ring.We give an example to indicate this.

Throughout this paper,R denotes an associative ring with identity 1.As usual J(R) denotes the Jacobson radical of the ring R and U(R)the group of units in R.We write Tn(R)for the ring of all upper triangular n×n matrices over the ring R.Let G denote a group.Then a group G is called a p-group if every element of G is a power of p,where p is a prime.Let Snstand for the symmetric group of degree n.The ring of integers is denoted by Z,and we write Znfor the ring of integers modulo n.

2 Clean Group Rings

A group G is called locally finite if every finitely generated subgroup is finite.Lemma 2.1Let R be a ring,G a group,and△(G)⊆J(RG).ThenProof.Write B={γ∈RG|ε(γ)∈J(R)}.

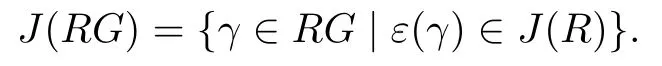
“⊆”.It is obvious that ε(J(RG))⊆J(R)since ε is an epimorphism,and thus J(RG)⊆B is clear.

“⊇”.Since B is an ideal of RG,it suffices to show that 1+γ has a right inverse in RG wherever γ∈B.1+ε(γ)is invertible in R,since γ∈B implies ε(γ)∈J(R).It follows that there is a β∈R such that

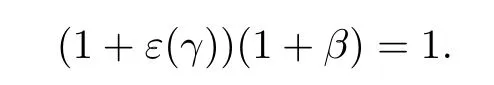
Since ε is epimorphic,there also exists a β′∈RG such that ε(β′)=β.So we have

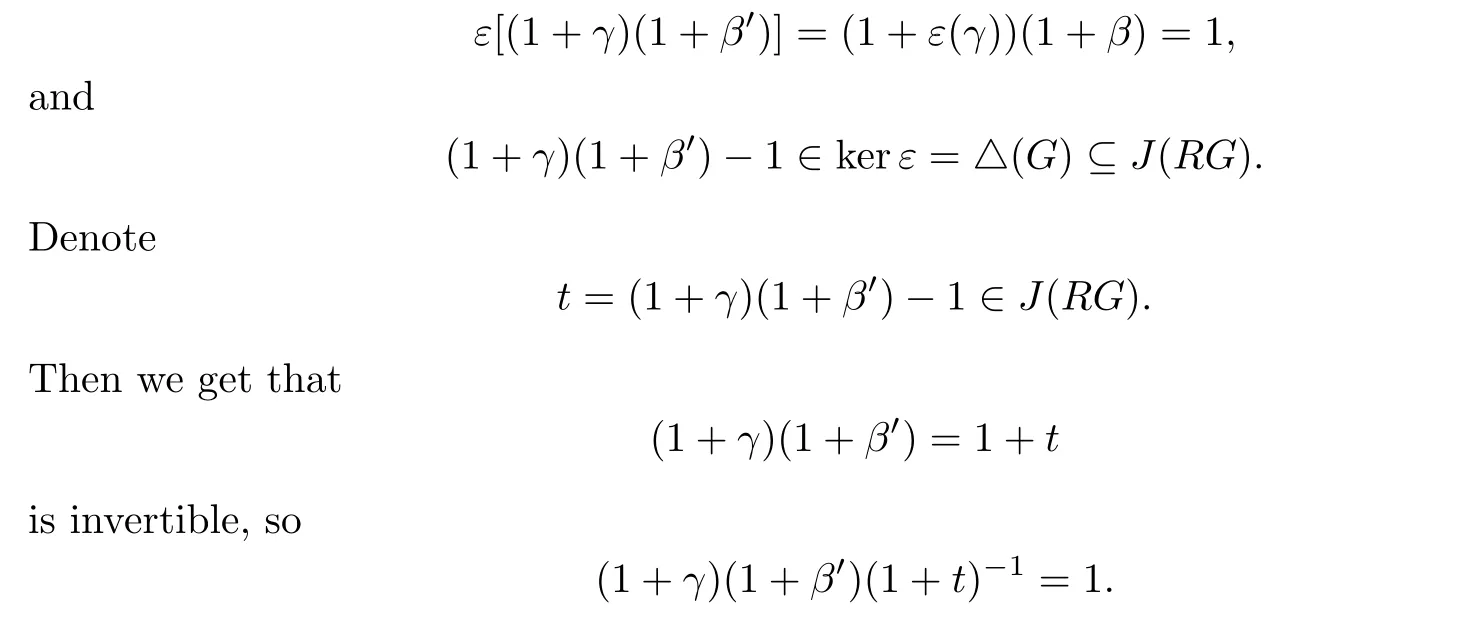
We say that idempotents lift modulo an ideal A of a ring R if whenever α2−α∈A, there exists e2=e∈R such that e−α∈A.

Lemma 2.2If R is a clean(exchange)ring,G is a locally finite group,and△(G)⊆J(RG),thenRGis clean(exchange).

Proof.We know that R is a clean(exchange)ring if and only if R/J(R)is clean(exchange), and idempotents can be lifted modulo J(R).

In this spirit,we first prove RG/J(RG)is clean(exchange).Since G is a locally finite group,it implies

is clean as R is clean.

Next we prove idempotents can be lifted modulo J(RG).

For any α∈RG such that

Since R is clean(exchange),it follows that there is e2=e∈R⊆RG such that

Then e−α∈J(RG)by Lemma 2.1.

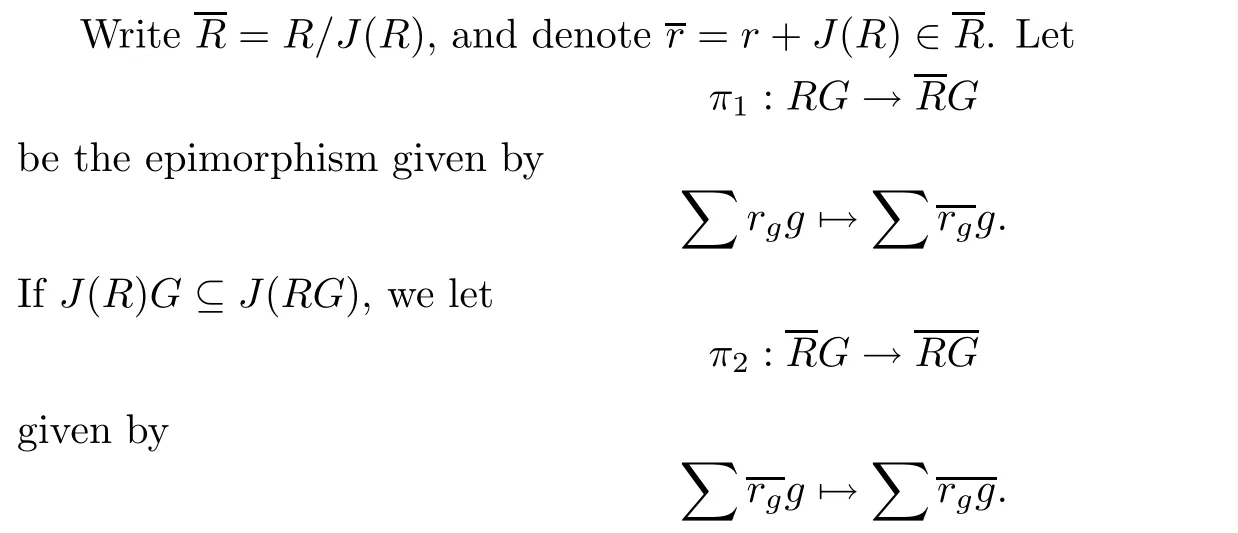
Lemma 2.3Let R be a ring and G a locally finite group.Then

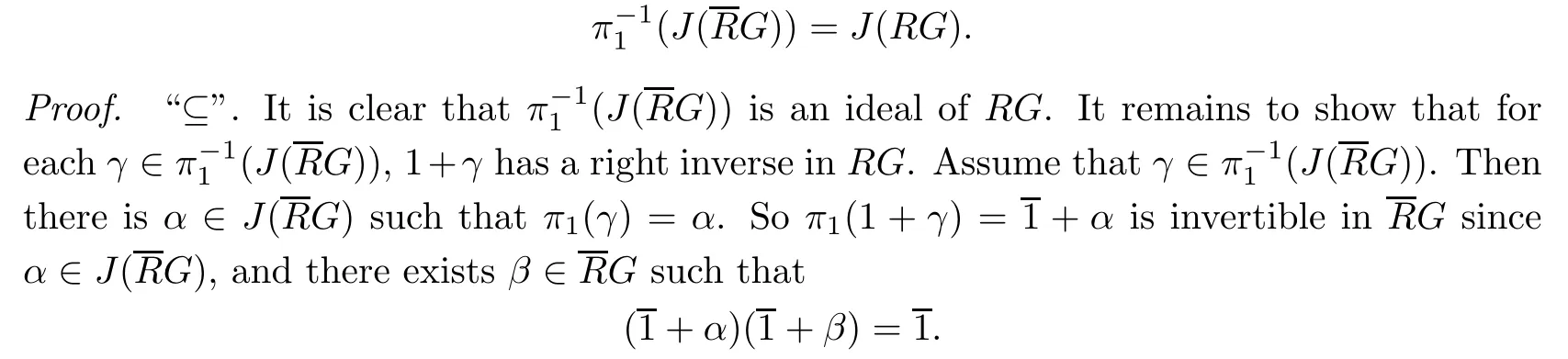
As π1is an onto ring morphism,there also exists β′∈RG such that π1(β′)=β.So we have

Theorem 2.1Let R be a ring withchar=p＞0and G a locally finite p-group.If R is clean,then so is RG.

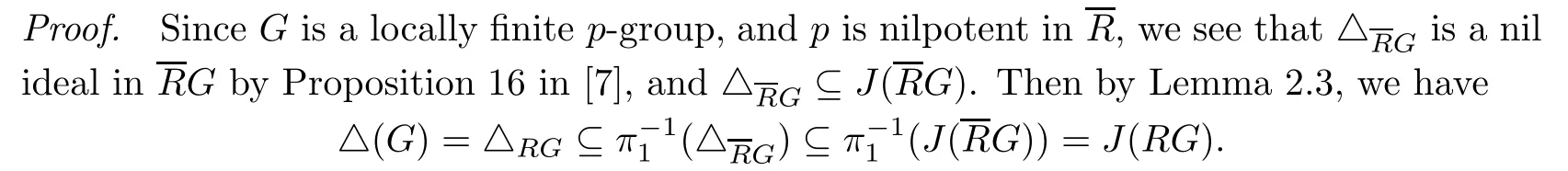
So RG is clean by Lemma 2.2.The proof is completed.

More generally,we have the following results.

Theorem 2.2Let R be a ring withcharR=p＞0,G a locally finite group,N the normal p-subgroup of G,and H any subgroup of G such thatNH=G.If RH is clean,then so is RG.

Proof.Assume that g∈G.By G=NH,there are n∈N and h∈H such that

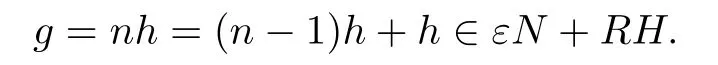
And then we have

Let π:RG→RG be the canonicial homomorphism.Since G is a locally finite group, we have J(R)G⊆J(RG),so the following de fi nitions of mappings are reasonable.Let

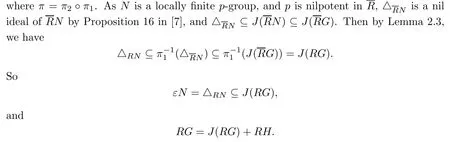
On one hand,by the de fi nition of π,there is

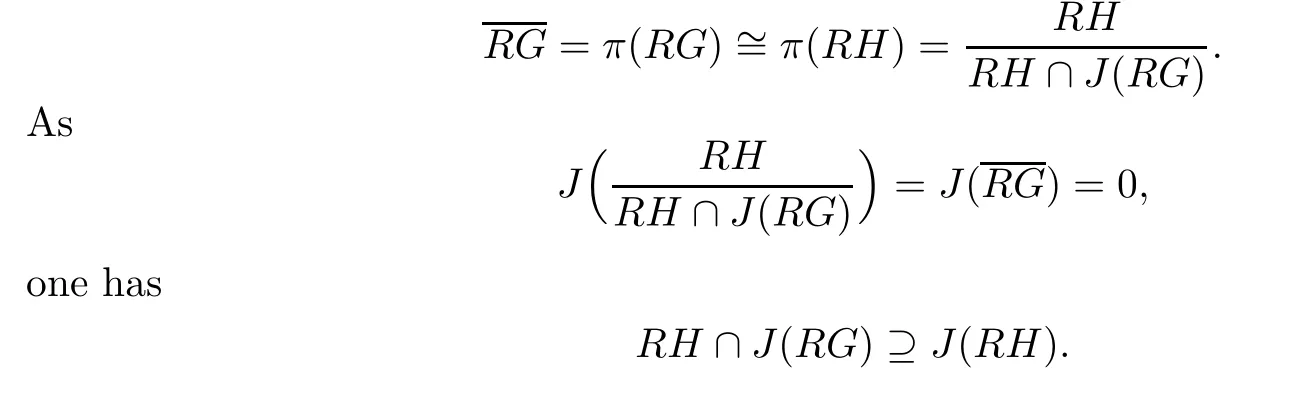
On the other hand,we also have RH∩J(RG)⊆J(RH)by Proposition 9 in[7].Then

Now,it suffices to prove that idempotents can be lifted modulo J(RG).Let

For any α∈RG such that α2−α∈J(RG),there holds that

since ω is an epimorphism.Since RH～=R(G/N)and RH is clean,there is

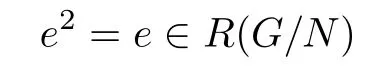
Lemma 2.4Let R be a ring,G a group,N a normal subgroup of G,andεN⊆J(RG). Let

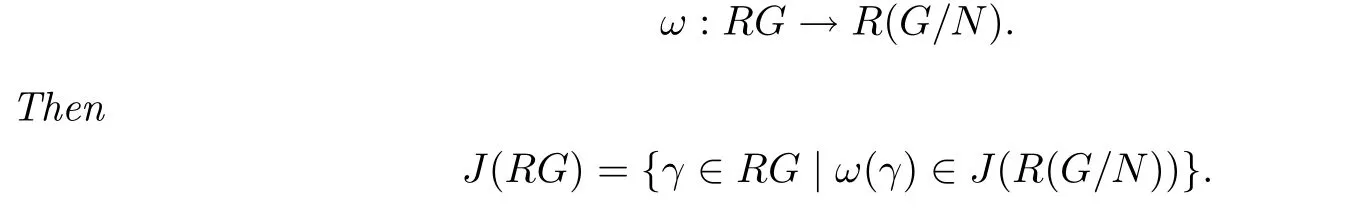
Proof.Write B={γ∈RG|ω(γ)∈J(R(G/N))}.

“⊆”.It is obvious since ω(J(RG))⊆J(R(G/N)).

“⊇”.Since B is an ideal of RG,for each γ∈B,it remains to prove that 1+γ has a right inverse in RG.The rest of the proof is similar to that of Lemma 2.1.

Example 2.1Let

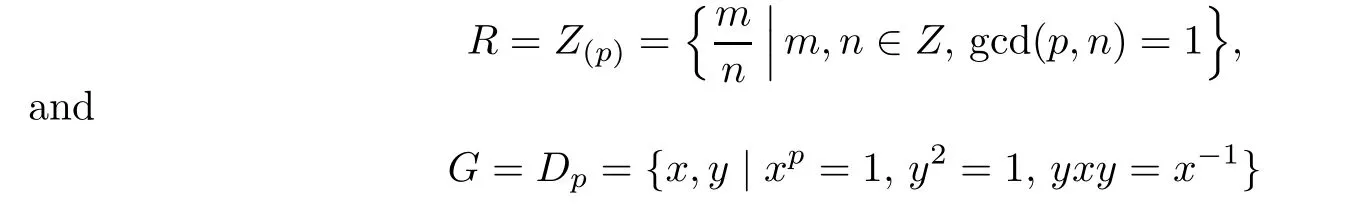
be the dihedral groups of order 2p.Then the group ring RG is clean.

Proof.By Theorem 2.2,it remains to prove that Z(p)C2is clean.

If p=2,then Z(p)C2is a local ring,and so it is clean.

3 USC Group Rings

Lemma 3.1IfRG/J(RG)is boolean,then△(G)⊆J(RG).

Proof.Suppose that RG/J(RG)is a boolean ring.It implies that for any g∈G,(1−g)2−(1−g)is in J(RG),that is,g2−g∈J(RG),and hence

Corollary 3.1([6],Proposition 24)If the group ringRGis USC,then R is USC and G is a2-group.

Proof.Suppose that RG is USC.R as an image of RG is strongly clean.Moreover,R is a subring of RG,which implies R is USC and 2∈J(R).As RG is USC,it follows that RG/J(RG)is boolean.Then△(G)⊆J(RG)by Lemma 3.1,which implies G is a p-group and p∈J(R)by Proposition 15 in[7].If p=2k+1 is an odd prime,by p,2∈J(R),we have

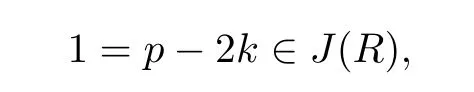
which is impossible since 1 is a unit of R.Then p must be equal to 2.

Lemma 3.2LetRbe a USC ring and G be a group.If△(G)⊆J(RG),then RG is USC.

Proof.Assume that R is a USC ring.Then for any α∈RG,ε(α)∈R and there exists a unique idempotent e∈R⊆RG such that

As eε(α)=ε(α)e,it follows that

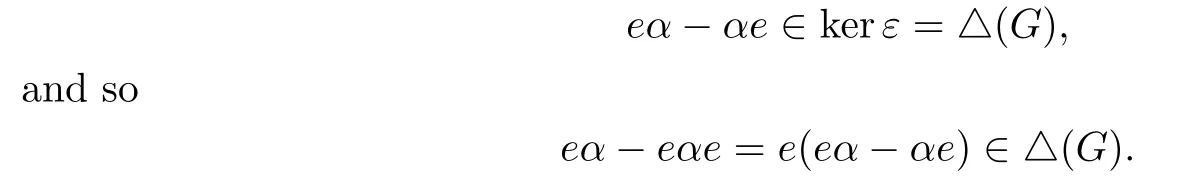
By calculation,we have that

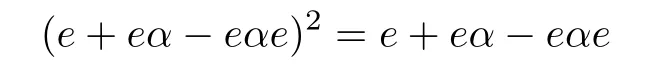
is an idempotent of RG.

Since

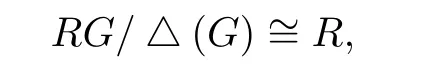
the idempotent of RG has the form e+△(G),where e is an idempotent of R.Let j∈△(G). If e+j∈RG is an idempotent,then we have

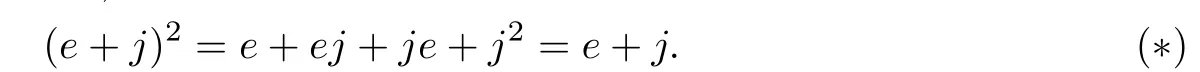
Multiplying the equation(∗)by e from the left hand(right hand)side,we have eje+ej2=0 (eje+j2e=0).Hence

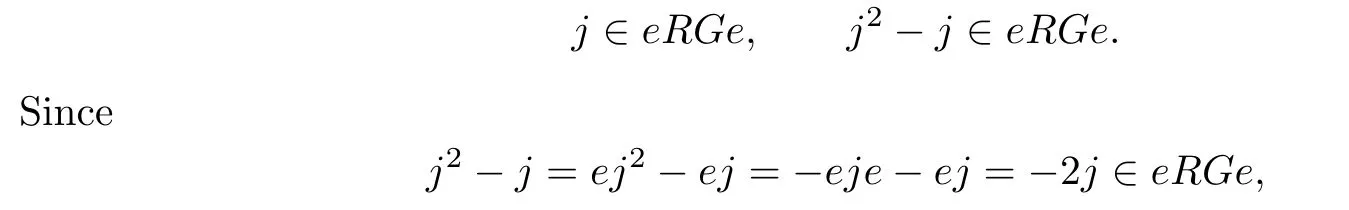
we obtain that j2=−j∈eRGe,and j4=j2∈△(G)⊆J(RG)is an idempotent.It follows that−j=j2=0 since there is no non-zero idempotent in J(RG).Then the idempotents of RG are all in R.

From the former description,we have eα−eαe=0,which implies eα=eαe.Similarly, we also have αe=eαe.Then αe=eα.

Now we see ε(e−α)=e−ε(α)∈J(R).By Lemma 2.1,we have e−α∈J(RG).

Next,we prove e is unique.Assume that there is another idempotent f∈RG(then in R)such that f−α∈J(RG).Then

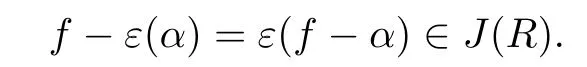
We have e=f since R is a USC ring.

Theorem 3.1LetRbe a ring,andGa locally finite group.ThenRGis USC(uniquely clean)if and only ifRis USC(uniquely clean)andGis a2-group.

Proof.Necessity can be proved by Corollary 3.1.

Sufficiency.Suppose that R is a USC(uniquely clean)ring.Then R/J(R)is boolean and charR=2.By using Theorem 2.1,we have△(G)⊆J(RG).Then RG is USC(uniquely clean)by Lemma 3.2(see Corollary 3.5 of[9]).

Remark 3.1This is why T2(Z2)D4is USC in Example 26 of[6],since T2(Z2)is a USC ring,and D4is a 2-group as a dihedral group of order 8.

Corollary 3.2If R is a ring and G a locally finite group,then the following statements are equivalent:

(1)RGis a USC group ring;

(2)Ris USC,and△(G)⊆J(RG);

(3)Ris USC,andJ(RG)/△(G)J(R);

(4)Ris USC,andRG/J(RG)R/J(R);

(5)Ris USC,andGis a2-group.

Proof.(1)⇒(2)is clear by Lemma 3.1 and Corollary 3.1.

(2)⇒(1)follows from Lemma 3.2.

(2)⇒(3)⇒(4)⇒(2)are clear since G is a locally finite group implies J(R)G⊆J(RG).

(1)⇔(5)can be proved by Theorem 3.1.

4 Uniquely Exchange Group Rings

In PH.D dissertation“clean rings and regular local rings”(see[10]),Ying[10]studied the (left)uniquely exchange ring.It was proved that an element of a ring R is called left uniquely exchange,if for any x∈R there exists a unique idempotent e∈Rx such that 1−e∈R(1−x).R is called left uniquely exchange ring if every element of R is left uniquely exchange.The right uniquely exchange element and right uniquely exchange ring can be de fi ned accordingly.We call an element or a ring uniquely exchange if it is both left and right uniquely exchange.We know that left exchange ring and right exchange ring are equivalent.But for both left and right uniquely exchange rings,this is not true.In that article,Ying[10]proved that R is a left uniquely exchange ring,then R/J(R)is boolean and 2∈J(R),and also gave the following relations:

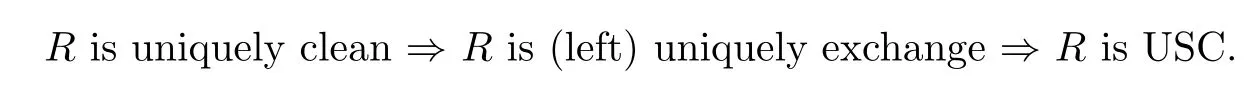
For the uniquely clean group rings and the USC group rings,we obtain the parallel result,i.e.,Theorem 3.1.Naturally,we consider the(left)uniquely exchange group rings. As a middle ring,does the uniquely exchange group ring also possess this property?

Next,we give an example to indicate that this property is not fi t for the left uniquely exchange group rings,and so is the uniquely exchange group rings.

Theorem 4.1LetRbe a boolean ring.ThenT2(R)C2is not uniquely exchange whileT2(R)is uniquely exchange.

Proof.Assume that R is a boolean ring.Then,we see that T2(R)is uniquely exchange since T2(R)is uniquely exchange if and only if R is boolean by Corollary 2.2.3 of[8].We have known that T2(R)C2T2(RC2).So,it remains to prove RC2is not a boolean ring. As RC2is uniquely clean,and all its idempotents are in R.Moreover,R⊂RG,i.e.,RG contain elements which are not idempotent.Thus,RC2is not boolean.

[1]Nicholson W K.Lifting idempotents and exchange rings.Trans.Amer.Math.Soc.,1977,229: 269–278.

[2]Anderson D D,Camillo V P.Commutative rings whose elements are a sum of a unit and idempotent.Comm.Algebra,2002,30:3327–3336.

[3]Nicholson W K,Zhou Y.Rings in which elements are uniquely the sum of an idempotent and a unit.Glasgow.Math.J.,2004,46:227–236.

[4]Nicholson W K,Zhou Y.Clean general rings.J.Algebra,2005,291:297–311.

[5]Nicholson W K.Strongly clean rings and Fitting’s lemma.Comm.Algebra,1999,27:3583–3592.

[6]Chen J,Zhou W,Zhou Y.Rings in which elements are uniquely the sum of an idempotent and a unit that commute.J.Pure Appl.Algebra,2009,213:215–233.

[7]Connell I G.On the group ring.Canad.J.Math.,1963,15:650–685.

[8]Chen J,Nicholson W K,Zhou Y.Group rings in which every element is uniquely the sum of a unit and an idempotent.J.Algebra,2006,306:453–460.

[9]Wang X.Cleanness of the group rings of Abelian p-group over a commutative ring.Algebra Colloq.,accepted.

[10]Ying Z.Clean Rings and Regular Local Rings.PH.D.dissertation.Nanjing:Southeast Univ., 2009.

Communicated by Du Xian-kun

16S34,16N40

A

1674-5647(2012)01-0017-09

date:March 10,2009.