On Some Varieties of Soluble Lie Algebras∗

NAN JI-ZHU,WANG CHENG-CHENG AND LI HAI-LING

(School of Mathematical Sciences,Dalian University of Technology, Dalian,Liaoning,116024)

On Some Varieties of Soluble Lie Algebras∗

NAN JI-ZHU,WANG CHENG-CHENG AND LI HAI-LING

(School of Mathematical Sciences,Dalian University of Technology, Dalian,Liaoning,116024)

In this paper,we study a class of soluble Lie algebras with variety relations that the commutator of m and n is zero.The aim of the paper is to consider the relationship between the Lie algebra L with the variety relations and the Lie algebra L which satis fies the permutation variety relations for the permutation φ of{3,···,k}.

variety,permutation,nilpotent class

1 Introduction

There are many parallel results between groups and Lie algebras.We can translate some results from groups to Lie algebras.For example,Macdonald[1]discussed some varieties of groups,particularly,some varieties associated with nilpotent groups in 1961,and then Suthathip[2]showed the similar varieties for nilpotent Lie algebras.In this paper,we extend similar varieties in[3]to soluble Lie algebras.

Let L be a Lie algebra,and x1,x2,···,xn∈L.The commutator[x1,x2,···,xn]in L is de fi ned by

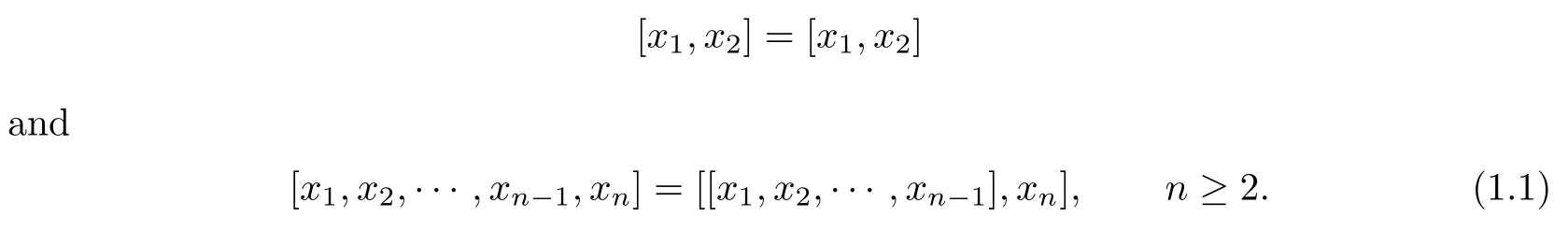
Moreover,we de fi ne

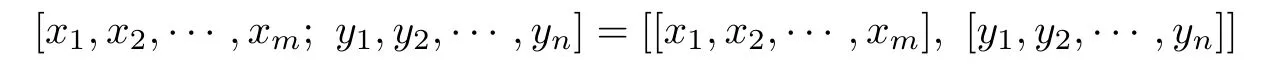
for any integers m and n.We say that the Lie algebra L is variety[m,n]=0 if it satis fies

If a Lie algebra L satis fies[x1,x2,···,xk]=[x1,x2,xφ(3),···,xφ(k)],where φ is a permutation of{3,···,k},then we call that L satis fies C(k,φ).If L satis fies C(k,φ)for all permutations φ of{3,···,k},then we call that L satis fies C(k).

The main result of this paper is that L satis fies C(n+2)(n≥2)if and only if L satis fies the law[n−k,2+k]=0 for all k=0,1,···,n−2.Then it is easy to see that[3,2]=0 is equivalent to C(5).Furthermore,[n,2]=0(n≥3)implies C(2n−1).However,the law [m,n]=0 does not imply any nontrivial law C(k,φ)for m,n≥3.

2 The Lie Algebra with Varieties[m,n]=0

Now we want to introduce some properties of the Lie algebra with variety[m,n]=0.Denote by(x)a subalgebra generated by x.

De fi nition 2.1LetLbe a Lie algebra.We de fi ne the sequence{Ln}n≥1by

L1=L, Ln+1=[L,Ln], n≥1.

IfLm+1=0,Lm0for somem,then we say thatLhas nilpotent class preciselym.

Lemma 2.1[4]LetAbe an associative algebra.Then the following identities hold:

Lemma 2.2[3]IfLsatis fies[n,m]=0,then[n+p,m+q]=0for any nonnegative numberspandq.

Lemma 2.3[5]IfLsatis fiesC(k,φ1)andC(k,φ2),thenLsatis fiesC(k,φ)for anyφin the group generated byφ1andφ2.

Lemma 2.4[5]IfLsatis fiesC(k),thenLsatis fiesC(m)for allm≥k.

Lemma 2.5LetLbe a Lie algebra.Then[a,[x,y]]=0if and only if[a,x,y]=[a,y,x]for anya,x,y∈L.

Proof.It is easily checked by Jacobian identity.

Lemma 2.6LetLbe a Lie algebra with variety[n,2]=0(n≥2).IfL/Z(L)satis fiesC(n+1),thenLsatis fiesC(n+2).

Proof.By Lemma 2.5,we know that L satis fies C(n+2,φ1)for φ1=(n+1,n+2).Since L/Z(L)satis fies C(n+1),in particular,it satis fies C(n+1,φ2)for φ2=(3,4,···,n+1).

Thus,for any x1,x2,···,xn+1∈L,we have

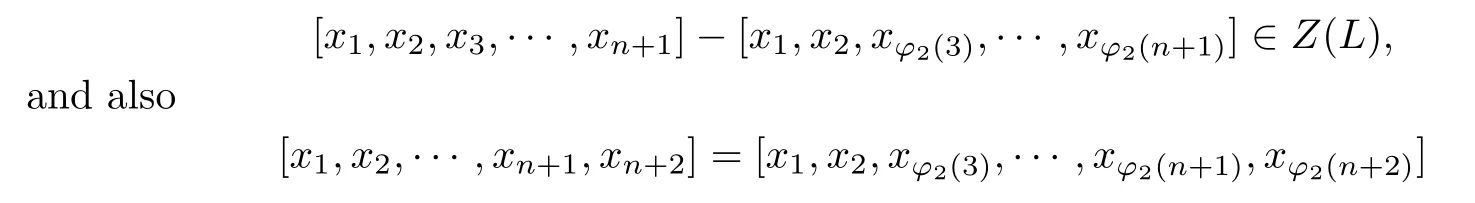
for any xn+2∈L.That is,L satis fies C(n+2,φ2).Since Sn=hφ1,φ2i,by Lemma 2.3,we know that L satis fies C(n+2).

Lemma 2.7IfLsatis fies[n,m]=0and[n−1,m+1]=0,thenL/Z(L)satis fies[n−1,m]=0.Particularly,ifLsatis fies[n,n−1]=0,thenL/Z(L)satis fies[n−1,n−1]=0. Proof.Let

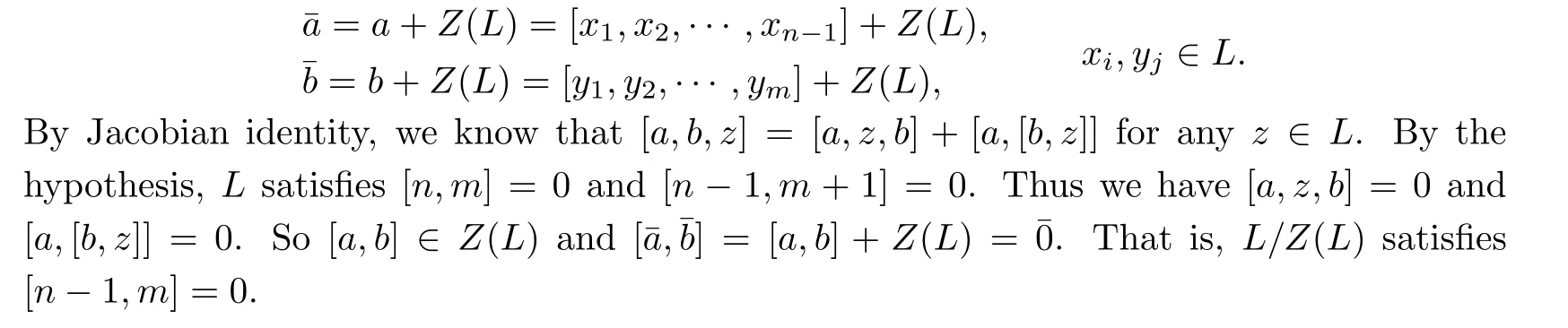
Lemma 2.8IfLsatis fies[n,m]=0andL/Z(L)satis fies[n−1,m]=0,thenLsatis fies[m+1,n−1]=0.

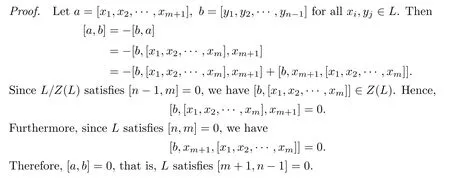
3 Some Cases for Small m and n

In this section,we consider the construction of the Lie algebra L with variety[m,n]=0 for small m and n.

Theorem 3.1Lsatis fies[3,2]=0if and only ifLsatis fiesC(5).

Proof.If L satis fies[3,2]=0,then by Lemma 2.7,L/Z(L)satis fies[2,2]=0.Thus, L/Z(L)satis fies C(4).Thereby,by Lemma 2.6,the result is true.

Conversely,if L satis fies C(5),in particular,L satis fies C(5,φ1)for φ1=(4,5).Using Lemma 2.5,the result follows.

Corollary 3.1Lsatis fiesC(n)if and only ifLsatis fiesC(n,φi)(i=1,2)forφ1= (4,5,···,n−1)andφ2=(n−1,n),wheren≥5.

Proof.If L satis fies C(n),then it is easy to see that L satis fies C(n,φi),i=1,2.

Conversely,let L satisfy C(n,φi),i=1,2.We proceed by induction on n.If n=5,it is the result in Theorem 3.1.By Lemma 2.3,L satis fies C(n,φ)for any φ such that φ(3)=3. Since L satis fies C(n,φ1),we have[x1,x2,x3,···,xn−1,xn]=[x1,x2,xφ1(3),···,xφ1(n−1),xn] for any xn∈L.Hence,

That is,L/Z(L)satis fies C(n−1,φ1).Similarly,we can show that L/Z(L)satis fies C(n−1,φ3)for φ3=(n−2,n−1)∈hφ1,φ2i.By induction on n,L/Z(L)satis fies C(n−1). Thus,by Lemma 2.6,L satis fies C(n).

Theorem 3.2Lsatis fiesC(n+2)(n≥2)if and only ifLsatis fies[n−k,2+k]=0for allk=0,1,···,n−2.

Proof.Induction on n.In the cases of n=2 and n=3,it has been proved in Theorem 3.1.Now,we assume n＞3.If L satis fies C(n+2),then L satis fies[n,2]=0 by Lemma 2.5.Furthermore,L satis fies C(n+2,φ)for any φ which fi xes n+2.Thus,

for any xn+2∈L,and then

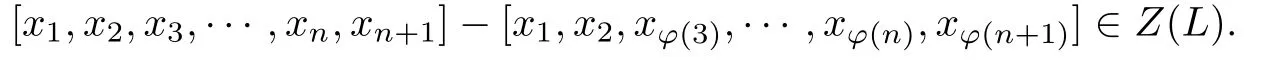
So we know that L/Z(L)satis fies C(n+1).Then,by the hypothesis of induction on n, L/Z(L)satis fies[n−1−k,2+k]=0 for any nonnegative integer k such that n−1−k≥2. Finally,by Lemma 2.8 and[n,2]=0,we know that L satis fies[n−k,2+k]=0 for all k=0,1,···,n−2.

Conversely,let L satisfy[n−k,2+k]=0 for all nonnegative integers k≤n−2 and assume by induction that if L satis fies[n−1−k,2+k]=0 for all 0≤k≤n−3,then L satis fies C(n+1).Since L satis fies[n−k,2+k]=[n−k−1,2+k+1]=0,and L/Z(L) satis fies[n−k−1,2+k]=0 by Lemma 2.7,L/Z(L)satis fies C(n+1).Hence,L satis fies C(n+2)by Lemma 2.6.

Remark 3.1By the anticommutativity of Lie bracket,we know that L satis fies[n,m]= 0 if and only if L satis fies[m,n]=0.Thus,we can replace Theorem 3.2 by the following result:L satis fies C(n+2)if and only if L satis fies[n,2]=[n−1,3]=···=[n−s,2+s]=0, where 2s=n−2 if n is even and 2s=n−3 if n is odd.

Theorem 3.3IfLsatis fies

for somek＜s,thenLsatis fiesC(2n−2k−1).

Proof.Let L satisfy(3.1).Then,by Lemma 2.2,L satis fies

also.By Theorem 3.2,we know that L satis fies C(2n−2k−1).This completes the proof.

In particular,for k=0,we get the following results.

Corollary 3.2IfLsatis fies[n,2]=0,thenLsatis fiesC(2n−1)forn≥3.

Corollary 3.3IfLsatis fiesC(n,φ)(n≥5)for allφwhich leave fixed3,···,m(m≤n−2),or for any set of generators of the group of permutations of{m+1,···,n}(m≥3),thenLsatis fiesC(n+m−3).

Theorem 3.4LetLsatisfy

where0≤k1≤k2≤···≤km≤sandsis de fi ned in Remark3.1.ThenLsatis fiesC(n+1+t),wheret=max{k1,k2−k1,···,km−km−1,s−km}.

Proof.Note that(3.1)implies(3.2),and(3.3)implies that L satis fies[n+t−1,2]= [n+t−2,3]=···=[2,n+t−1]=0.Hence,L satis fies C(n+1+t)by Theorem 3.2.This completes the proof.

Next,we comment brie fl y on some results of the situation for

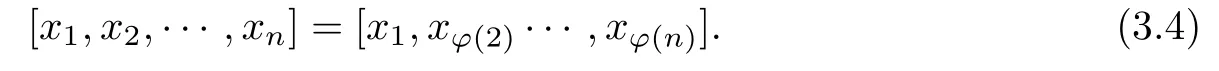
Theorem 3.5Lsatis fies(3.4)for all permutationsφof{2,···,n}if and only ifLis a nilpotent of class≤n−1.

Proof.Use induction on n.For n=3,by Lemma 2.5,[x1,x2,x3]=[x1,x3,x2]if and only if[x1,[x2,x3]]=0.If L satis fies the hypotheses for n＞3,then L satis fies[n−2,2]=0 by Lemma 2.5 and L satis fies(3.4)for any φ which fi xes n.Thus,as in the proof of Lemma 2.6, L/Z(L)satis fies(3.4)when n is replaced by n−1 for any permutation φ of{2,···,n−1}. Therefore,by induction,L/Z(L)is a nilpotent of class≤n−2 and L is a nilpotent of class≤n−1.

The proof of the converse is trivial.

Now,we know that the law[n,2]=0(n≥3)implies C(2n−1).The law[n,1]=0 means that nilpotence class n implies C(n+1)trivially.However,the law[m,n]=0(m,n≥3) does not imply C(k,φ)for any k and any nontrivial φ.It suffices to show this for[3,3]=0.

Lemma 3.1IfLsatis fies[3,3]=0andC(n,φ)(n≥4),whereφ(m)=3,m3,then the two-generator subalgebras ofLsatisfyC(n+1).

Proof.If n=4,then it is easy to see that L satis fies C(4).Now,let n≥ 5,m=n and H=(x,y),x,y∈L.Then,we show that H satis fies[n−1,2]=0.Since L satis fies [3,3]=0,it suffices to check that[x1,x2,···,xn−1,[x,y]]=0.Since L satis fies C(n,φ)and φ(n)=3,we can assume that φl(3)=n.Thus

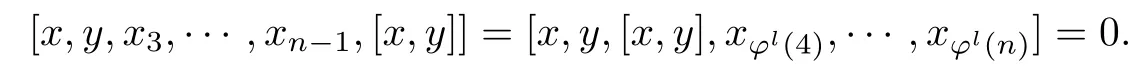
If x1=[x,y],then by Jacobian identity we have

Since φ(n)=3,

We have

By the same way,we know that

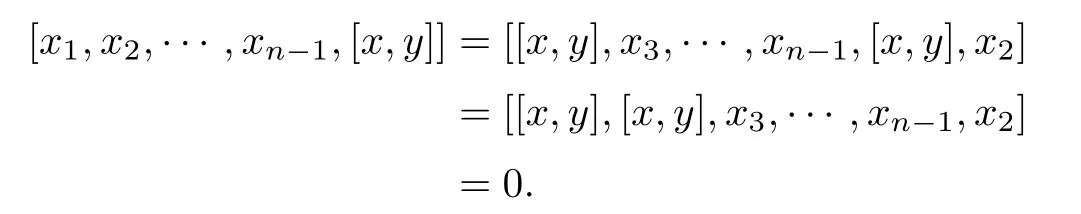
Since[3,3]=0,H satis fies[n−1,2]=0.And since L satis fies[n−2,3]=[n−3,4]=···= [3,n−2]=0,by Theorem 3.2,H satis fies C(n+1).

Now we consider the case of m＜n.We proceed by induction on n−m.Suppose that the result is true for the case of φ(m+1)=3,m2,then we need to consider the case of φ(m)=3(m3).By the hypothesis of induction,we know that H/Z(H)satis fies C(n) and[n−2,2]=0.Since H satis fies[n−2,3]=0,by Lemma 2.8 we know that H satis fies [n−1,2]=0.Thus[3,3]=0 implies that H satis fies C(n+1).This completes the proof.

Next,we give a Lie algebra which satis fies[3,3]=0,but the subalgebra(x,y)does not satisfy C(n+1)for any n≥4.

Let A(Z,3)be the associative algebra of formal power series in the noncommuting variables x,y,z with integer coefficients.Let[r1,r2]=r1r2−r2r1.Then A(Z,3)can be viewed as a Lie algebra.If the relation r1[r2,r3]=0 is added to A(Z,3)for any monomials ri∈A(Z,3),whenever the degree(as monomial in x,y,z)of r1is≥3,then the result that A(Z,3)satis fies[3,3]=0 follows.

Now,we only need to show that[[r1,r2,r3],[r4,r5,r6]]=0 for any ri∈A(Z,3).Let [r1,r2]=a,[r4,r5]=b.Then we have

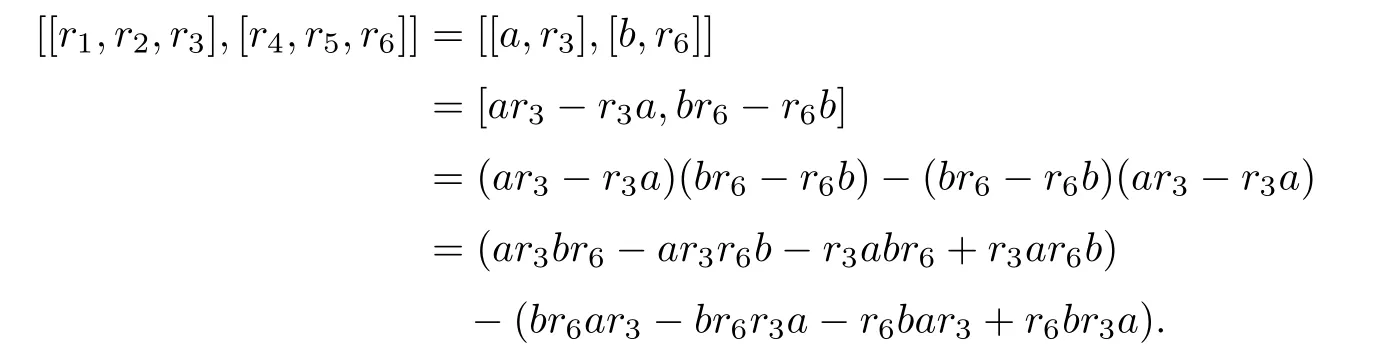
In the expression(ar3br6−ar3r6b−r3abr6+r3ar6b),we replace a and b by r1r2−r2r1and [r4,r5],respectively.And in the expression(br6ar3−br6r3a−r6bar3+r6br3a),we replace a and b by[r1,r2]and r4r5−r5r4,respectively.Then we have[[r1,r2,r3],[r4,r5,r6]]=0. That is,A(Z,3)satis fies[3,3]=0.

We show that the subalgebra H=(x,y)does not satisfy C(n+1)for n≥4.By Lemma 2.1,we know that

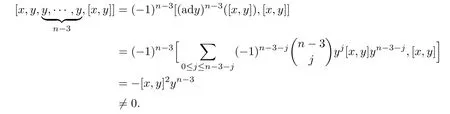
By Lemma 2.5,we have

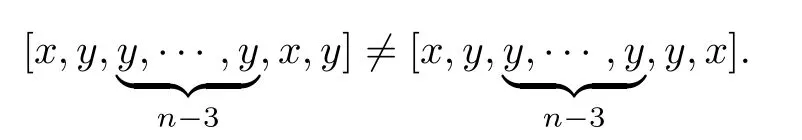
So(x,y)does not satisfy C(n+1)for any n≥4.

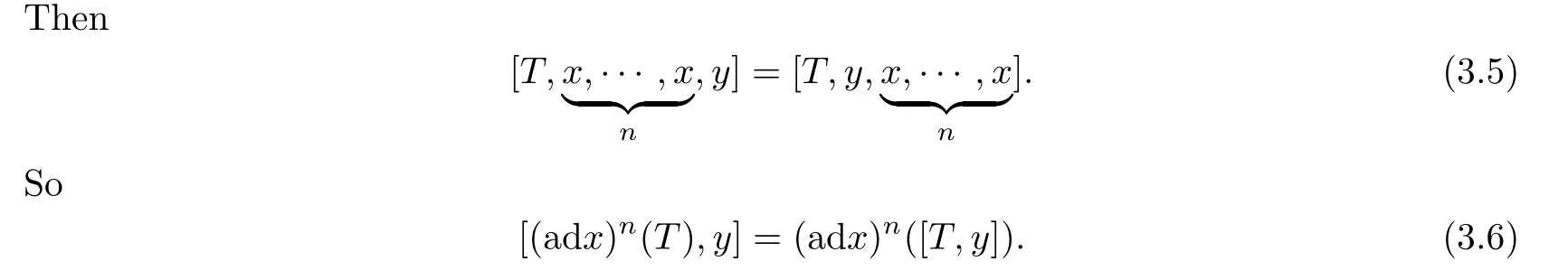
By Lemma 2.1,we know that the equality(3.5)holds if and only if n=0.Hence,we have proved the following remark.

Remark 3.2The law[m,n]=0(m,n≥3)does not imply C(k,φ)for any k≥4 and nontrivial φ.

[1]Macdonald I D.On certain varieties of groups.Math.Z.,1961,76:270–282.

[2]Suthathip S.On the Relationship Between the Class of a Lie Algebra and the Classes of Its Subalgebra.Raleigh:North Carolina State Univ.,2007.

[3]Levin F.On some varieties of soluble groups I.Math.Z.,1964,85:369–372.

[4]Strade H,Farnsteiner R.Modular Lie Algebras and Their Representations.New York:Dekker, 1988.

[5]Levin F.On some varieties of soluble groups II.Math.Z.,1968,103:162–172.

Communicated by Du Xian-kun

17B30

A

1674-5647(2012)01-0010-07

date:Jan.19,2010.

The NSF(10671028)of China.