新型永磁转子偏转式三自由度电机磁场特性分析

李 争，郭智虎，张 玥

（河北科技大学电气工程学院，河北石家庄 050018）

新型永磁转子偏转式三自由度电机磁场特性分析

李 争，郭智虎，张 玥

（河北科技大学电气工程学院，河北石家庄 050018）

在简述永磁转子偏转式三自由度电机的工作原理和优越性能的基础上，针对该新型永磁多自由度电机的结构提出了气隙磁场的计算方案，建立了球坐标下标量磁位和气隙磁通密度的计算公式。同时基于三维有限元软件，建立起转子磁场模型并进行仿真计算，给出了不同充磁模式下的磁通密度分布情况，与解析计算结果进行了对比验证。理论分析和计算结果表明了所设计结构的有效性，转子易于实现三自由度偏转运动，其结果可为进一步的研究和实验设计提供借鉴和参考。

永磁体；多自由度；解析法；三维磁场；有限元法

随着工业技术的进步，人工智能设备得到了迅猛发展，机械系统日益复杂化和精密化，像在机器人关节和眼睛等部件，需要完成多个自由度的运动。虽然由多个单自由度电机和机械传动机构组合到一起能够实现多自由度的运动，但是系统体积庞大，并且级联传动机构的误差也会影响设备的精密度。因此人们开始研究能够实现多自由度运动的设备与装置［1－2］。随着稀土永磁材料性能的不断提高，对永磁多自由度电机的研究和开发成为当前的热门问题［3－10］。永磁转子偏转式三自由度电机是一种利用转子上分布的永磁体和定子上通电线圈的相互作用，使转子产生三自由度运动的永磁电机。这种电机主要应用于航空、航天、机器人和仿生学等领域。它克服了传统电机的多球轴承支撑、摩擦力大、运动方向单一等缺点，具有很高的研究价值［11］。

笔者在提出一种新型永磁转子偏转式三自由度电机结构的基础上，采用解析法和有限元法对其永磁转子的磁场进行对比分析，可为同类型电机的深入研究提供理论依据和实验参考。

1 永磁转子偏转式三自由度电机的结构和工作原理

1.1 三自由度电机的结构

本文研究的三自由度电机有限元模型如图1所示，电机整体轴向高度为17.5 mm，电机上下两层定子间距为5.5 mm，外径为90 mm，内径为78 mm；磁极由带铁芯线圈通电构成，磁轭高度和厚度均为6 mm；转子半径为15.5 mm，保持定转子之间气隙为0.5 mm。作为初步模型，定转子磁极数量分别为6极和4极配合，以保证驱动的连续性和控制的灵活性。

1.2 三自由度电机的工作原理

电机的工作原理是以通电线圈产生的磁场与永磁体磁场之间的相互作用为基础的［12－13］。电机线圈标号如图2所示。给2和5′号线圈加载直流电，使其产生磁极为N极，给2′和5号线圈加载电流，使其产生磁极为S极，如图2a）所示。同性的磁极产生相互排斥的作用力，异性的磁极产生吸引的作用力，合成的电磁力矩使得电机转子完成绕X轴偏转的运动。图2b）为电机绕X轴偏转运动的截面示意图。

给3，4，1′和6′线圈加载电流，使其产生的磁极为S极，给3′，4′，1和6线圈加载电流，使其产生的磁极为N极，合成的电磁力矩使得电机转子绕Y轴作偏转运动，如图3所示。

同理，给1，1′，4和4′线圈加载电流使其产生的磁极为S极，给3，3′，6和6′线圈加载电流使其产生的磁极为N极，电流产生的S极磁极对永磁转子N极有切向拉力分量，电流产生的N极磁极对永磁转子N极有切向推力分量，合成的切向电磁力矩使得电机做绕Z轴的旋转运动。根据电机转子不同的位置，使电流控制器对相应的线圈通入电流，电机即可实现连续Z轴的旋转运动。图4给出电机绕Z轴旋转的示意图。

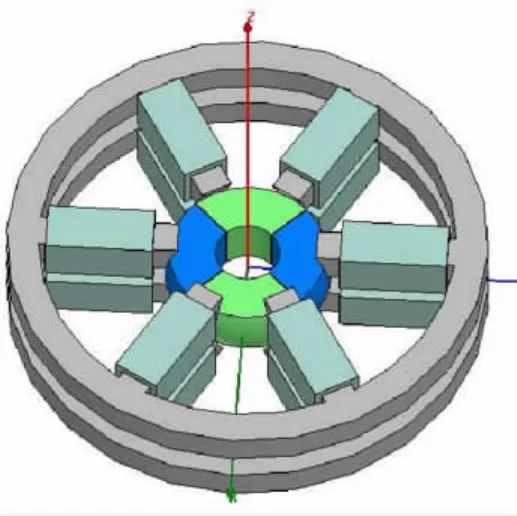
图1 三自由度电机有限元模型Fig.1 FEM model of the 3-DOF motor

图2 绕X轴偏转工作原理及其截面Fig.2 Principle of deflection type motion around the X axis and the section view

由于所设计的三自由度电机受到结构的限制，绕X和Y轴偏转运动被迫限制在一定的角度范围内。改变电机线圈通电电流的方向，电机可实现反方向的运动。

2 电机永磁转子磁场解析分析

电磁场分析在永磁电机设计和参数计算中发挥着重要作用。用解析法分析电磁场结果为显式，对于物理概念表达清楚，在定性方面具有优势，且能直观地得出磁场分布与电机主要结构参数之间的关系。永磁转子磁极产生的磁场是气隙磁场的重要组成部分，所以对永磁转子磁极磁场有必要进行分析［14］。表1给出了永磁转子的主要计算参数。

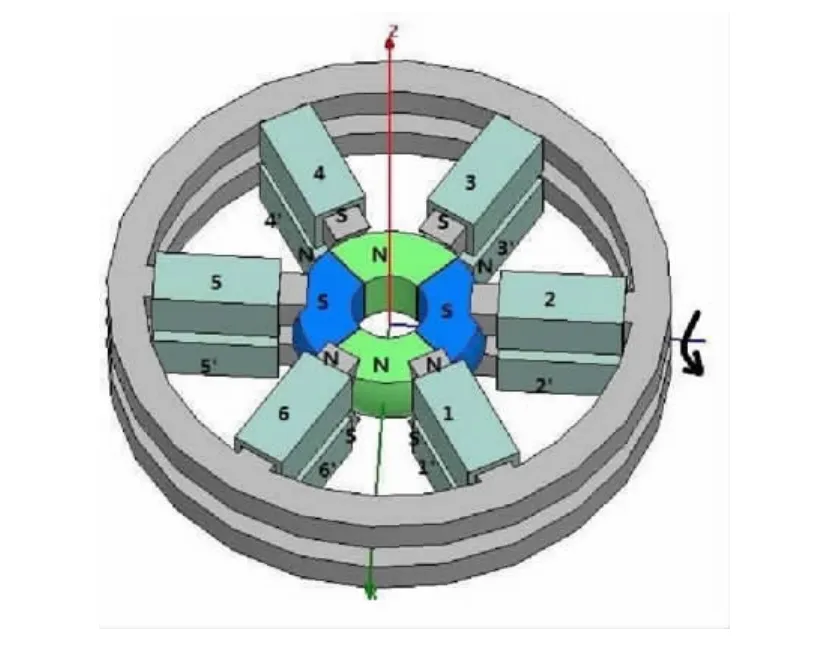
图3 绕Y轴偏转Fig.3 Deflection type motion around the Y axis

图4 绕Z轴旋转Fig.4 Deflection type motion around the Z axis

2.1 标量磁位通解

电机永磁转子的磁场求解问题可化为在一定边界条件下对拉普拉斯方程求解。在球面坐标下的拉普拉斯方程为

2.2 气隙磁通密度

通过标量磁位的通解，可以得到气隙磁通密度B1为

将磁场沿φ和θ方向的谐波考虑进去，可得B11r随φ和θ变化的曲面图，如图5所示。

图5 圆鼓形转子B11r分布图Fig.5 B11r distribution of the drum type rotor

图6 B11r随φ的变化Fig.6 Changes of B11r withφ

由图5中可以看出，B11r随φ和θ按曲面余弦波变化，沿赤道1周具有2个正峰值点和2个负峰值点，这与4极鼓形转子磁体结构是一致的。当θ＝π／2时，B11r的变化如图6所示。从图6中可以看出，当θ固定时，B1r的基波分量B11r沿φ方向按正弦规律变化。2个波峰之间相距180°，其峰值为0.513 5 T，电角度为机械角度的2倍。

3 电机永磁转子磁场有限元分析

3.1 电机转子几何参数和永磁体材料参数

电机永磁转子有限元模型如图7所示，电机转子整体结构成鼓形。鼓形转子所在球的半径R＝15.5 mm，电机转子厚度为10 mm，中心位置半径为5 mm的圆柱体，用以安置输出轴；电机转子2对磁极即N极和S极围绕Z轴交替排列，磁极间距为0.2 mm。

永磁体有2种电流模拟方法，体电流密度模拟和面电流密度模拟，线性永磁体一般用磁体表面上的等效电流模拟。线性永磁材料关系表达式为

式中M p为永磁体磁化强度，μr为永磁体相对磁导率，H c为铁磁材料矫顽力。

式中Br为永磁体剩余磁感应强度，μ0为真空磁导率。

由上述的关系式可知，参数M p，μr，H c和Br只有2个是相互独立的，在定义线性永磁材料时，只需给出2个参数，另外2个参数就可以根据关系式计算得到。本文中，电机转子永磁材料选择线性钕铁硼材料，给定永磁体相对磁导率μr为1.02，矫顽力H c为－890 k A／m，通过计算可知永磁体极化强度M p为907.8 k A／m，剩余磁感应强度为1.14 T。

3.2 永磁体充磁方式

电机转子永磁体的充磁可以采用径向充磁、轴向充磁和平行充磁3种方式。径向充磁就是在球面坐标系下，以鼓形所在球的球心为起点，磁体磁化方向沿着R轴方向向四周延伸；轴向充磁是在柱面坐标系下，以Z轴为轴线，磁体磁化方向沿着ρ轴方向；平行充磁是在空间直角坐标系下，磁体磁化方向沿着某一坐标轴，充磁方向垂直于另外2个轴所组成的平面。下面以单个永磁体磁极N极为例，给出磁极3种充磁方式下的磁密矢量分布俯视图，如图8－图10所示。

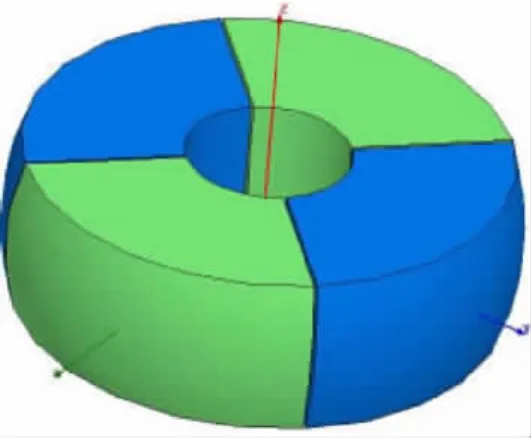
图7 电机永磁转子有限元模型Fig.7 PM rotor model

图8 径向充磁Fig.8 Radial magnetization mode

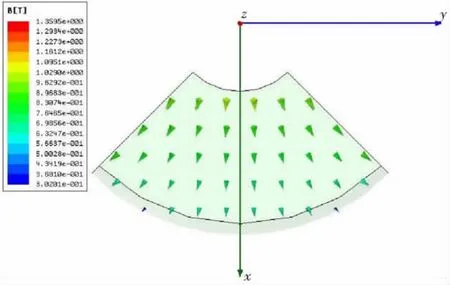
图9 轴向充磁Fig.9 Axial magnetization mode

3.3 电机永磁转子磁场有限元分析

采用的有限元分析软件对电机的磁场进行建模计算。下面以轴向充磁方式为例，分析电机转子永磁体在轴向充磁方式下产生的磁场。电机永磁转子磁密矢量图如图11和12所示。

图11 电机永磁转子俯视磁密矢量图Fig.11 Overlooking flux density vector

在以电机永磁转子赤道外0.2 mm的圆周为路径（起点为与X轴的交点，方向为逆时针），也就是在球面坐标下θ＝90°的位置，计算获得的磁感应强度幅值曲线如图13所示。与图5的基波幅值对比可以看出，2种方法计算获得的数据基本吻合，在峰值位置和幅值水平上较为一致，也充分验证了计算分析这类特殊近球形永磁体产生磁场所采用方法的正确性。

4 结 论

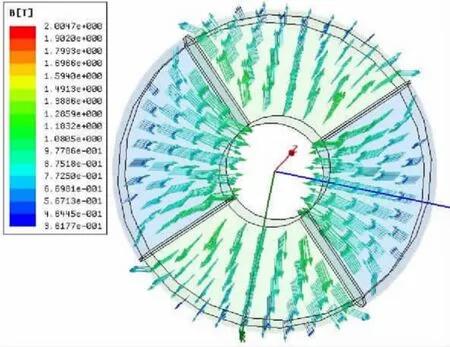
图12 电机永磁转子三维磁密矢量图Fig.12 3D flux density vector

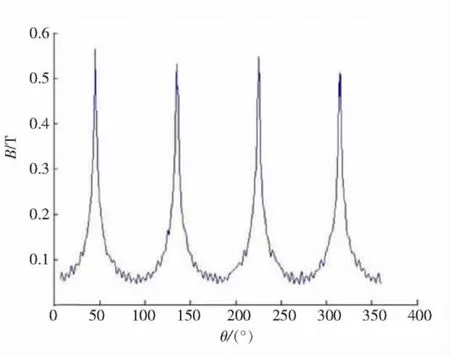
图13 φ＝90°时磁密幅值图Fig.13 Magnitude values of flux density whenφ＝90°

在提出的一种新型多自由度永磁电机结构的基础上，探讨了永磁转子气隙磁场的计算与分析方法，包括解析计算法和三维有限元方法，给出了具体的计算结果，分析和比较了轴向、径向磁化方向下的磁通密度分布，从而能够为电机实现自转和偏转运动的转矩计算提供依据。计算结果对比验证了设计的有效性，为永磁转子偏转式三自由度电机的进一步设计与优化提供了借鉴和参考。永磁体与定转子结构参数优化和控制策略设计是下一步的工作内容。

［1］李 争，王群京.永磁多维球形电动机的研究与发展现状［J］.微特电机（Small Special Electrical Machines），2006，33（10）：7-11.

［2］吴立建.稀土永磁球形电动机的研究［D］.合肥：合肥工业大学，2004.

［3］YONGSU U M，TORNOAKI YANO.Characteristic of torque on spherical stepping motor based on hexahedron-octahedron structure［C］.Proceedings of the International Conference on Mechatronics and Automation［C］.Kagawa：［s.n.］，2008.170-175.

［4］DEHEZ B，GALARY G，GRENIER D，et al.Development of a spherical induction motor with two degrees of freedom［J］.IEEE Transactions on Magnetics，2006，42（8）：2 077-2 089.

［5］YUSUF O，AHMET A.Computer aided design and 3D magnetostatic analysis of a permanent magnet spherical motor［J］.Journal of Applied Science，2007，7（22）：3 400-3 409.

［6］李洪凤.Halbach阵列永磁球形电动机三维磁场分析［D］.天津：天津大学，2008.

［7］LEE Kok-Meng Lee，SON Hungson.Distributed multipole models for design and control of PM actuators and sensors［J］.IEEE／ASME Transactions on Mechatronics，2008，13（2）：228-238.

［8］DAVID S，EDWARD R，GREGORY S C.mathematical models of binary spherical-motion encoders［J］.IEEE／ASME Transactions on Mechatronics，2003，8（2）：234-244.

［9］万山明，黄生华，傅光洁，等.空间坐标系中的三维电动机［J］.中国电机工程学报（Proceedings of the CSEE），1998，18（5）：305-309.

［10］王群京，钱 喆，李 争，等.基于机器视觉的永磁球形步进电动机转子位置检测方法［J］.中国电机工程学报（Proceedings of the CSEE），2008，28（36）：73-78.

［11］王群京，李 争，夏 鲲，等.新型永磁球形步进电动机结构参数及转矩特性的计算与分析［J］.中国电机工程学报（Proceedings of the CSEE），2006，26（10）：158-165.

［12］郭立炜，赫苏敏，傅占稳.旋转电机的机电耦合电路［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2000，21（1）：77-80.

［13］李彦新.电磁力的作用和电磁转矩的产生［J］.河北工业科技（Hebei Journal of Industrial Science and Technology），2001，18（3）：10-12.

［14］LI Zheng.Robust control of PM spherical stepper motor based on neural networks［J］.IEEE Transactions on Industrial Electronics，2009，56（8）：2 945-2 954.

［15］LI Zheng，WANG Yong-tao，ZHAO Zhe.Computation and analysis of a novel spherical actuator based on 3D finite element simulation［J］.Journal of Information ＆ Computational Science，2010，7（12）：2 410-2 419.

Magnetic field analysis of a novel 3-DOF deflection type PM motor

LI Zheng，GUO Zhi-hu，ZHANG Yue
（College of Electrical Engineering，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

Based on the brief introduction of the operation principle and superior performance of PM deflection type three-degrees-of-freedom motors in this paper，the new PM motor air-gap magnetic field calculation schemes have been presented and the scalar magnetic flux density calculation formula in the spherical coordinate are established.The rotor magnetic field model is built in 3D finite element software and computed with simulation to derive the flux density distribution under different magnetization modes.The results by these two methods are compared and validated.The theoretical analysis and computation results demonstrate the effectiveness of the designed structure；the rotor is easy to achieve three-degrees-of-freedom deflection motion，which can provide references for further research and experimental design.

permanent magnet；multi-DOF；analytical method；3D magnetic field；FEM

TM341

A

1008-1542（2012）05-0422-07

2012-09-08；责任编辑：李 穆

国家自然科学基金资助项目（51107031）；河北省自然科学基金资助项目（E2009000703）；河北省高等学校科学研究计划项目（Z2010135）

李 争（1980-），男，河北石家庄人，副教授，博士，主要从事特种电机及其控制方面的研究。